基于改进HHT的电压闪变检测*

倪良华，肖李俊，吕干云，历馨

（南京工程学院电力工程学院，南京211167）

0 引 言

电网中分布式电源的大量接入以及各种非线性、冲击性和波动性负荷的投入，加剧了电网中的电压波动［1］，电网中的电压闪变频繁出现，给工业生产和社会生活造成严重影响。供用电企业都希望检测到准确的电压闪变参数，从而有针对性地加装补偿设备进行电压闪变治理，以改善电能质量。

近年来，电压波动和闪变检测问题已逐渐成为研究热点，IEC给出了衡量闪变强度值的检测原理框图，学者们根据框图提出了多种计算短时闪变、长时闪变的计算方法，但这些方法不适用于时变电压闪变信号的检测。目前常用的闪变检测方法主要有平方解调法、小波变换法［3］，FFT分解法［4］、Hilbert变换法和S变换法［2］等等。文献［3］采用小波包分析与拟同步检波的方法，虽可提取电压闪变包络、高频细节以及突变时间，但如何选择合适的小波基仍需进一步研究。文献［4］采用FFT方法检测闪变信号，但对于闪变频率非FFT频率分辨率整数倍的闪变信号，采用FFT方法会产生栅栏效应，从而影响结果的准确性。文献［5］中使用Teager能量算子对电压闪变信号进行辨识，此方法对低频部分的闪变信号具有较高的辨识准确度，但对高频部分闪变信号，辨识准确度却较低。文献［6］采用原子分解法检测电压闪变信号，其检测参数的准确度较高，但是计算量大，运行时间较长。文献［7］首先使用数学形态滤波将闪变信号中的谐波与噪声等干扰信号滤除，然后采用Hilbert变换方法求出闪变包络线。不过数学形态学的滤波效果受选取的结构元素以及形态滤波器结构的影响，且使用Hilbert变换方法不能直接得到闪变的参数。文献［8］提出Prony与Hilbert相结合的方法，选择基于Hilbert变换的算法对电压波动信号进行检测，引入扩展Prony算法估计出信号频率参数，但抗噪能力不理想。文献［9］采用HHT方法进行电压闪变参数辨识，但该方法中的EMD存在着模态混叠以及端点飞翼现象，使得分解出的IMF分量不理想，严重影响了闪变参数检测的准确度。

针对HHT算法中EMD分解出的IMF分量不理想而导致闪变参数检测误差较大的问题，基于四点插值细分算法与HHT算法，提出了改进HHT的电压闪变检测方法。通过借助四点插值细分算法“分裂”新的控制点供三次样条插值拟合包络线，优化了EMD的“筛选”过程。仿真结果表明，采用四点插值细分算法改进的HHT方法能够有效降低噪声的干扰，且对模态混叠问题有一定的抑制作用，提高了最终检测出的闪变参数准确度。

1 电压闪变信号的数学模型

电压闪变分为周期与非周期性闪变，其中周期性电压闪变对电力系统危害最大，所以主要研究周期性电压闪变。

周期性电压闪变信号可抽象地看成以工频电压为载波，受到电压闪变分量为调幅波的调制，其数学形式为［10］：

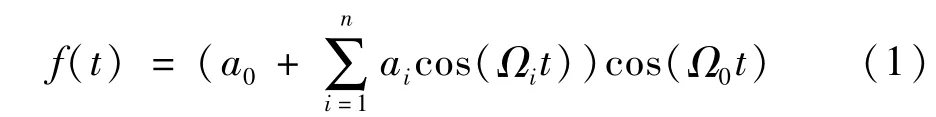
式中a0、Ω0分别是工频载波电压幅值及角频率；而ai、Ωi分别是调幅波电压的幅值及角频率；Ωi的取值范围为人对电压波动的觉察范围，一般取0.05 Hz～35 Hz。

2 HHT基本原理

HHT是一种信号处理方法，可以用于处理非平稳、非线性信号。该方法首先通过使用EMD将多分量信号分解为一组IMF分量，然后使用Hilbert变换对每个IMF分量进行分析处理，最终得到每个IMF分量的幅值与频率［11］。

2.1 经验模态分解

经验模态分解（EMD）的本质是通过一系列计算，将一个非平稳非线性信号转化为一组平稳的固有模态函数（IMF）分量。其中，每个IMF分量波形的上、下包络线均值为零，且零点与极值点数目相等或者相差为1。EMD具体计算过程如图1所示。

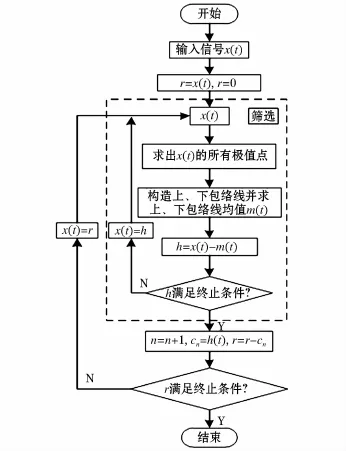
图1 EMD分解流程图Fig.1 Flow chart of EMD decomposition

从图1中可以看出，EMD分解过程主要为虚线框中的“筛选”步骤。即先在原信号数据序列中找出所有的极大值点与极小值点，随后使用三次样条插值算法分别对极大值点和极小值点数据序列进行拟合，此时得到相应的上包络线和下包络线，接着求出上、下包络线的均值，并用原信号数据序列减去它，从而得到一个新的信号数据序列，然后对产生的新的信号数据序列进行检测，若发现新的信号数据序列不满足IMF相关终止要求，则对该信号数据序列再进行一次“筛选”，直到满足要求后再进行下一步计算。

2.2 Hilbert变换

对一连续的电压闪变信号X（t），其Hilbert变换Y（t）为：

式中*表示卷积；t表示时间；τ表示积分分量。

电压闪变信号 X（t）的幅值 a（t），相位 θ（t）以及瞬时频率 f（t）可以通过式（3）～式（5）获得：

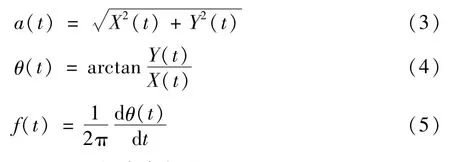
3 改进HHT闪变参数辨识原理

EMD在对闪变信号进行分解时，其中的“筛选”步骤产生的上、下包络线存在着过包络与欠包络问题，甚至有时还存在着“过冲”现象［12］。这些情况的出现，降低了分解出的IMF分量理想程度，使得最终通过Hilbert变换检测的闪变信号幅值和频率误差较大。

为此提出了一种改进HHT方法进行电压闪变参数检测，该方法主要是对EMD中的“筛选”步骤进行优化，即借助四点插值细分算法的“分裂”作用增加用于拟合上、下包络线的控制点，继而减缓了上、下包络线的过包络、欠包络和“过冲”问题，分解的具体过程如图2所示。通过此方法可以提升EMD分解的IMF分量的理想程度，并最终使闪变参数检测准确度得到提高。

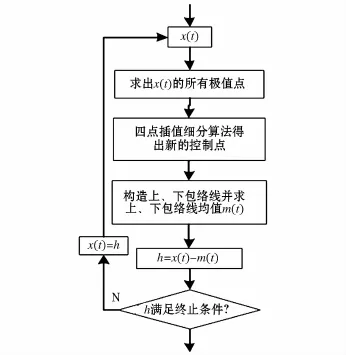
图2 优化的EMD中“筛选”步骤流程图Fig.2 Flow chart of“sifting”step in improved EMD

3.1 四点插值细分算法

四点插值细分算法是一种快速、离散的插值方法，该方法借助相邻的四个控制点来计算新控制点，且每次“分裂”都使用相同的运算规则，属于一种稳定的细分格式［13］。四点插值细分算法定义如下［14］。

根据下列细分规则，求出第k+1层的控制点。

其中ω为张量参数，一般取其为1/16时，拥有最佳的Holder正则性。为使细分迭代层数可控，可对控制点的总个数进行限制，具体个数视实际情况而定。经过多次验算，本文采用的四点插值细分算法“分裂”两次时效果最好，因此迭代层数设为两层。

图3 四点插值细分算法分裂图Fig.3 Split chart of four point interpolation subdivision algorithm

从图3中可以看出，第k+1层上的偶数序列的控制点为第k层上的旧控制点，而第k+1层上的奇数序列的控制点为第k层上相邻的四个旧控制点依据相关运算规则而求出的，这种情况与式（6）相对应。

3.2 改进HHT闪变信号检测

闪变信号在经过Hilbert变换处理后，分别得出工频载波幅值A0与频率f0以及去除直流分量的闪变包络值A（t）；然后使用添加四点插值细分算法的EMD方法对闪变包络信号进行分解，得到一组IMF分量；最后再次通过Hilbert变换求取每个IMF分量的幅值ai与频率fi。具体流程如图4所示。

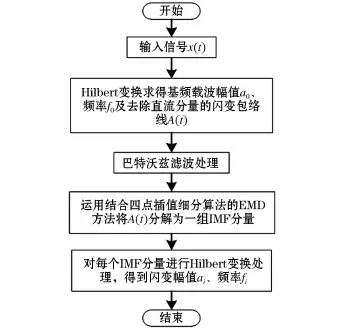
图4 改进HHT电压闪变参数检测流程图Fig.4 Flow chart of modified HHT detection method of voltage flicker

在运用优化的EMD分解过程中，求得极值点P0（x0，y0），P1（x1，y1），……Pn（xn，yn）（x0≤x1≤…≤xn，n≥5）后，令这些极值点为四点插值细分算法的初始控制点。随后用式（6）所示的细分规则分裂出新的控制点 Pn+1（xn+1，yn+1），Pn+2（xn+2，yn+2），……，Pm（xm，ym），m≥6。接着对包含分裂出的新控制点在内的所有控制点使用三次样条插值法进行拟合，并分别求出上、下包络线。此种方法可以有效缓解提取包络时出现的过包络、欠包络以及“过冲”问题，同时亦保留了三次样条插值具有二阶光滑度的优点［15］。

采用四点插值算法优化的EMD包络线提取效果如图5所示，从图中可以看出，采用了四点插值算法优化的EMD产生的包络线较之前未采用四点插值细分算法优化的EMD产生的包络线更加光滑，且在局部区域有效地缓解了对信号的欠包络、过包络现象，从而提升了包络的理想程度。

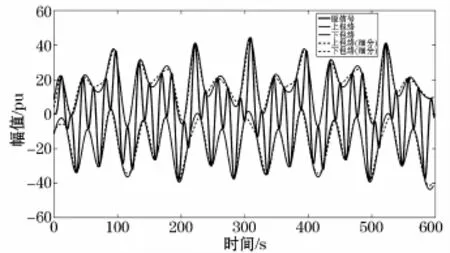
图5 EMD提取包络线对比示意图Fig.5 Comparison chart of EMD extract envelop

4 仿真分析

4.1 含噪声单一分量闪变信号

设信号表达式为：

信号中工频为50 Hz，调幅波频率为11 Hz，幅值为基频载波的0.1，同时在此信号基础之上，又添加了信噪比为20 dB的高斯白噪声。

首先使用Hilbert变换提取闪变信号包络，得到工频载波的频率与幅值，结果如表1所示。随后使用巴特沃兹滤波器对提取的调制分量包络进行滤波，接着通过使用HHT方法与改进HHT方法分别对此信号进行检测分析，得到结果如表2所示。在EMD分解过程中，采用四点插值细分算法而得的包络线与未采用四点插值细分算法而得的包络线对比情况如图6所示。

表1 Hilbert变换辨识的工频载波频率和幅值Tab.1 Frequency and amplitude of power frequency carrier identification based on Hilbert transform

表2 含噪声单一分量信号HHT与改进HHT检测Tab.2 Detection of single component signal with noise between HHT and modified HHT

图6 含噪声单一分量信号包络提取对比图Fig.6 Comparison chart of envelop extraction in single component signal with noise

从图6中可以看出，闪变信号成分较为简单，信号波形分布基本均匀，采用四点插值细分算法提取的包络线与未采用四点插值细分算法提取的包络线总体上是吻合的，但由于信号中存在噪声，因而图中从左至右第四和第五个波峰分布异常，在这种情况下可以看到采用四点插值细分算法提取的包络线较未采用四点插值细分算法提取的包络线更为光滑，且在局部减缓了欠包络与过包络问题。

从表1中可以看出，使用Hilbert变换算法得到工频频率与幅值参数检测准确度高，抗噪声能力较好。从表2中可以看出，改进HHT方法检测结果较未改进HHT方法检测得出调幅波的频率和幅值参数的误差小。同时对比表1可以发现，两种方法检测出的调幅波参数误差较表1都有一定升高，这是因为EMD分解过程受到了高斯白噪声的影响，从而导致分解的IMF分量理想程度较低，然而改进HHT方法有效地降低了噪声的干扰，提升了分解出的IMF分量的理想程度，从而使信号的频率与幅值的检测准确度得到提高。

4.2 多分量闪变信号

（1）不含噪声

设信号表达式为：

f（t）=220［1+0.04cos（28πt）］+0.1cos（60πt）+λ（t）］cos（100πt）

信号中工频为50 Hz，调幅波频率为14 Hz，幅值为工频载波的0.04，调幅波频率为30 Hz，幅值为工频载波的0.1。使用HHT方法与改进HHT方法的分别对此信号进行检测，得出的结果如表3所示。

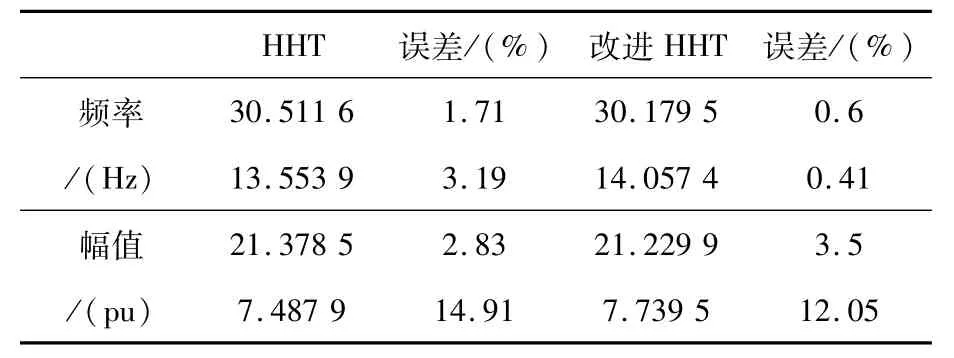
表3 多分量信号HHT与改进HHT检测Tab.3 Detection of multi-component signals between HHT and modified HHT

其中，在EMD分解过程中，增加四点插值细分算法而得的包络线与未增加四点插值细分算法而得的包络线对比情况如图7所示。

从图7可以看出，闪变信号成分较为复杂，波形分布较图6中的波形更为紧密。在相邻波峰或波谷分布间隔较大的区域，采用四点插值细分算法提取的包络线与未采用四点插值细分算法提取的包络线基本吻合一致，但是在相邻波峰或波谷分布间隔较小的区域，采用四点插值细分算法提取的包络线较未采用四点插值细分算法提取的包络线光滑度更好，且过包络与欠包络问题得到了缓解。

图7 多分量信号包络提取图Fig.7 Chart of envelop extraction in multi-component signals

从表3中可以看出，在对多分量闪变信号检测中，采用改进HHT算法的闪变频率检测准确度较未改进HHT算法的闪变频率检测准确度更高，优化效果明显，而在对闪变幅值检测时，在部分频域具有优化效果。同时，通过对EMD分解IMF分量数目的统计，改进HHT分解的IMF分量个数为4个，而未改进HHT分解的IMF分量个数为7个。由此可以看出，改进HHT算法中的EMD分解可以有效缓解模态混叠问题。

（2）含噪声

设信号表达式为：

f（t）=220［1+0.04cos（28πt）］+0.1cos（60πt）+λ（t）］cos（100πt）+λ（t）

该信号在多调制频率信号基础之上，添加了信噪比为20 dB的高斯白噪声。在使用Hilbert变换提取包络后，使用巴特沃兹滤波器进行滤波，随后通过使用HHT与改进HHT算法分别对此信号进行解析，得到结果如表4所示。

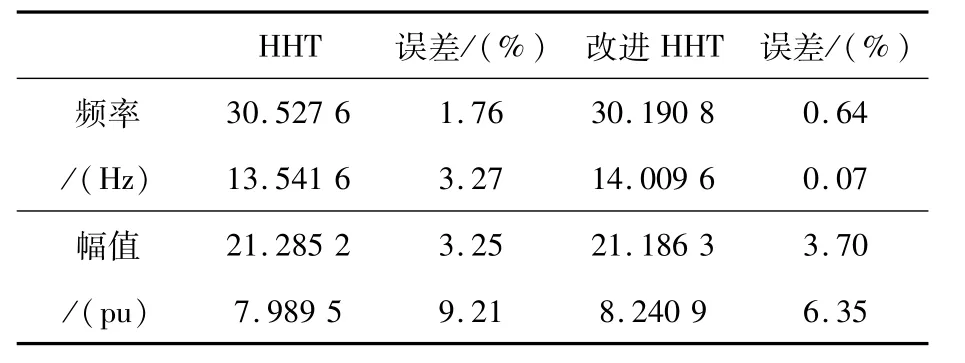
表4 多分量带噪声信号HHT与改进HHT检测Tab.4 Detection of multi-component signals with noise between HHT and modified HHT

在EMD分解过程中，采用四点插值细分算法而得的包络线与未采用四点插值细分算法而得的包络线对比情况如图8所示。

图8 含噪声多分量信号包络提取图Fig.8 Chart of envelop extraction in multi-component signals with noise

从图8可以看出，由于闪变信号成分复杂且包含有噪声分量，所以信号波形在局部波动较大。同时可以发现，采用四点插值细分算法与未采取四点插值细分算法提取的包络线的区别与图7类似。即在信号波形变化较为复杂的地方，采用四点插值细分算法提取的包络光滑度更好，过包络与欠包络问题得到了缓解。

从表4可以看出，在对闪变频率进行检测时，采用改进HHT算法检测的准确度与未采用改进HHT算法检测的准确度更高，而对闪变幅值进行检测时，改进HHT算法与未改进HHT算法相比，只在部分频域上的检测准确度出现提升。同时，通过对比表3与表4中的数据，发现闪变信号添加高斯白噪声后，采用未改进HHT算法检测闪变信号参数的准确度大部分出现了下降，而采用改进HHT算法的闪变信号参数检测的准确度并未出现明显变化。由此可得，改进HHT算法在对多分量闪变信号进行分析时，具有良好的抗噪能力。

5 结束语

针对应用HHT算法进行电压闪变参数检测过程中EMD分解出的IMF分量不理想而导致检测准确度不高的问题，提出了一种采用四点插值细分算法对HHT进行改进的电压闪变参数检测方法。通过四点插值细分算法“分裂”更多的控制点供三次样条插值算法拟合包络线，使包络线的过包络与欠包络问题得到缓解，优化了EMD的“筛选”过程，使EMD分解的IMF分量更加理想，从而最终提升了电压闪变参数的检测准确度。通过仿真计算，验证了所提方法具有一定优越性。研究结果表明：采用改进HHT算法检测电压闪变信号，可以更有效地降低噪声的干扰，对模态混叠具有一定的抑制作用。