基于外壳热分布的气体绝缘母线温度计算模型

李彦彰，舒乃秋，刘亚男，常怡东

（武汉大学电气工程学院，武汉430072）

0 引 言

三相共箱式气体绝缘母线（Gas Insulated Bus，GIB）采用将三相导体密封在充有SF6绝缘气体的金属壳体内来减小设备体积和提高运行可靠性。气体绝缘母线在运行过程中负荷电流和外壳涡流将引起设备发热，其温升特性是表征气体绝缘母线运行状态的重要指标，近年来出现多起由于导体过热引发的短路事故，导致停电而造成严重的经济损失和不良的社会影响［1］。三相共箱式气体绝缘母线过热故障已成为典型的故障，目前，尚无有效的监测手段及时发现三相共箱式气体绝缘母线的过热性故障，因此，研究三相共箱式气体绝缘母线的温升特性，对运行中的气体绝缘母线温升进行监测，预防气体绝缘母线过热性故障的发生，具有重要的工程意义和实用价值。

目前，气体绝缘母线的温升分析方法主要分为两类，一类是基于“场”的数值仿真法，一类是基于“路”的解析法。数值仿真法可获得包括气体绝缘母线最热点温度，整个求解区域内的温度分布以及热点温度的物理位置等信息。但该方法对气体绝缘母线结构参数要求较高，计算量大，实时性差，应用性不强，适合于科研的定性研究而不适合工程应用。相比于数值仿真法，热路模型计算法使用已知的简单模型代替复杂模型，计算参数较少，模型使用方便［2-6］。另外，热路模型的计算过程简单，采集数据后能够快速计算，只要建模足够准确，计算精度也相应较高［7］。故根据气体绝缘母线内部传热过程建立热路模型实时计算其温升的方法更适合于工程应用。张兴娟［8］等人建立了水力发电厂全连封闭母线的传热模型，计算了母线导体与外壳温度并确定了最有通风方案；Kim SW等［9-10］运用传统的传热分析以及热平衡方程组对离相GIB进行热计算；Ho S L等［11-12］通过努赛尔数求得自然对流的换热系数，采用电磁场-温度场耦合的有限元法对特高压气体绝缘母线进行计算；汪军衡［13］等建立了126 kV三相共箱式GIS母线等效热路模型，并利用单个指数函数模拟母线各组件的温升过程。

文章在分析三相共箱式气体绝缘母线的传热过程的基础上，基于热电类比原理建立了126 kV/2 kA三相共箱式气体绝缘母线等效热路模型。在建模过程中，针对三相共箱式气体绝缘母线的三相导体间温升相互影响的特性，引入气体绝缘母线对流换热系数和辐射换热系数进行计算。其中导体和外壳表面的对流换热系数采用计算流体力学方法进行拟合，导体、外壳以及环境之间的辐射换热值通过斯忒藩-波尔兹曼法求解；将导体和外壳的损耗作为热流源，导体和外壳间的导热、对流换热以及辐射散热等效为热阻；引入等效热容参数来描述气体绝缘母线的暂态温升过程；通过三相共箱式气体绝缘母线间隔进行原型物理温升试验，验证了三相共箱式气体绝缘母线热路模型的正确性和有效性，并得到了外壳-导体温升的数学关系式。

1 热电类比理论

无内热源稳态导热的温度场和热流密度描述方程分别如下：

式中 T为导体温度（℃）；q为导体热流密度（J/（m2·s）；λ为导体导热系数：

导电体中恒定电场和电流密度的描述方程分别如下：

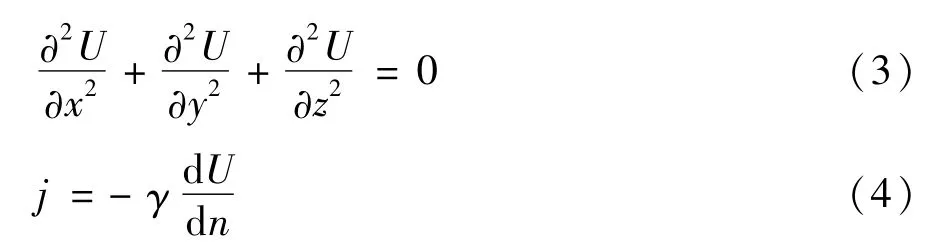
式中U为电压，V；j为电流密度，A/m2；γ为电导率。

根据模拟理论，若描述两个物理现象的微分方程遵循同一形式，且两个载体的几何形状和边界条件也类似，则两方程具有相同形式的解析解和实验解。对比式（1）和式（3），式（2）和式（4），可以看到两者具有完全相同的数学表达式，且各参量的结构形式也类似。热路和电路的物理量满足上述3个条件，因此可以参照电路的物理量形式来描述热路的物理量，这就是热电类比法的基本原理。电场与热场各参量的对应关系如表1所示。

表1 热路参数与电路参数类比关系Tab.1 Analogy quantities between thermal and electrical parameters

2 气体绝缘母线动态热路模型的建立

本论文所研究的126 kV/2 kA户内三相共箱式气体绝缘母线主要由三相导体、接头、绝缘盆子以及外壳等部分组成，且成水平布置，结构示意图如图1所示，导电杆与外壳均为铝合金材料。A、C相关于物理模型关于y轴水平对称，两相与x轴和y轴的距离相同；B相导体关于y轴对称，EB表示B相与x轴距离，为 130 mm。EA1=EC1，EA2=EC2，分别 A、C两相与x轴、y轴的距离，分别为130 mm、30 mm。

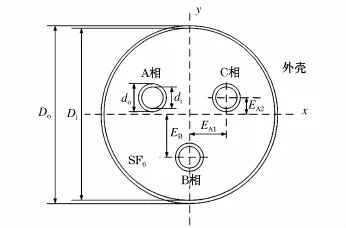
图1 GIS母线结构图Fig.1 Structure chart of GIS bus

运行中的气体绝缘母线热量主要由导体和触头产生的焦耳热损耗以及对应外壳中产生的涡流损耗组成［14-15］，热量使得母线导体和外壳的温度快速升高。由于三相导体和触头在传递热量中为良导体，导体和触头将热量迅速传递至导体外表面并且触头处产生的热量会沿导体轴向传递；热量由导体外表面通过自然对流传递至SF6气体，母线内部SF6气体温度较低，加热后的导电部件与作为冷却介质的气体之间存在温差，气体吸收一部分热量使其温度升高，形成气体流动，将热量传递至母线外壳；热量同时通过有限空间内面-面辐射的方式将热量传递至外壳；外壳在传递热量过程中也同样是良导体，将热量迅速传递至外壳的外表面；由于母线外壳与周围空气间存在温差，最终母线热量通过以自然对流和大空间辐射的方式耗散至周围空气中。

由于本文中导体与外壳同为铝材料，因此外壳带来的邻近效应损耗可以忽略不计。对于气体绝缘母线而言，导体厚度远小于导体直径，可以忽略厚度对邻近效应的影响。因此，三相导体总功率损耗为：

式中电阻R是由导体电阻和触头接触电阻Ra串联得到，其中接触电阻取值为14μΩ。

式中kΦ为导体的集肤效应系数；kb为三相导体各相邻近效应附加系数，可查表得出；I为三相导体内部电流有效值；R为单根导体的直流电阻值；θd为导体的摄氏温度；ρ为时铝材料的电阻系数；Ad为导体的截面积。

外壳的功率损耗为：

式中It为外壳环流电流的有效值；Rt为外壳直流电阻；kft为外壳的集肤效应系数。由于本文外壳厚度极小，所以近似取为1。

式中Et为感应电动势；At为外壳截面积；Lt为外壳电感；d′为三相导体的平均距离；D为外壳直径。

在对气体绝缘母线建立动态等效热路模型前，为建模和计算方便，在此做出如下假设：（1）忽略导体和外壳热传导过程，计算过程中可认为沿导体和外壳的温度是相同的，且忽略母线导体和外壳的热阻；（2）认为三相导体具有相同的电阻和热容，则三相导体产生相同的焦耳热损耗，即Ca=Cb=Cc，qa=qb=qc=1/3Qc。

在上述假设的基础上，建立如图2所示的气体绝缘母线动态等效热路模型。图中：qa、qb、qc、qt分别为三相导体的焦耳热损耗和外壳的涡流损耗；Ca、Cb、Cc、Cs、Ct分别导体、SF6气体及外壳热容；Ra、Rb、Rc、Rs、Rt分别为三相导体与SF6气体之间的热阻、外壳与SF6气体之间的热阻以及外壳与空气之间的热阻；θa、θb、θc、θs、θt、θ0分别三相导体、SF6气体、外壳以及环境的平均温度。

图2 气体绝缘母线动态等效热路模型Fig.2 Dynamic thermal-circuit model of GIB

根据热电类比理论，对于图2可列如下微分程：

3 模型参数

3.1 对流换热系数的计算

三相共箱式气体绝缘母线的对流换热系数计算式表示为：

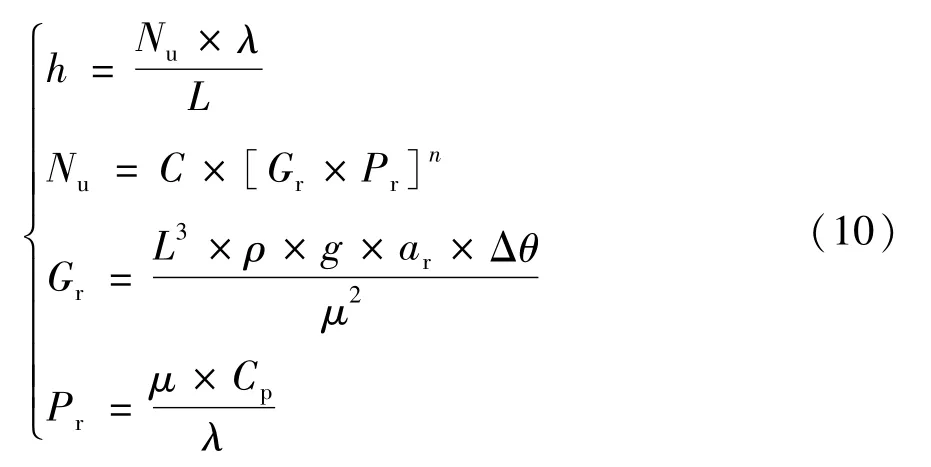
式中h为对流换热系数；Nu为努赛尔数；Gr为格拉晓夫数；Pr为普朗特数；C和n均为经验值；L为特征尺寸；λ为热传导率（W/m·K）；ρ为密度（kg/m3）；g为重力常数；αr为热膨胀系数（1/K）；μ为粘度（kg/m s）。

由于三相共箱式气体绝缘母线中A、B、C三相导电杆间温升通过绝缘气体SF6相互影响。因此，三相共箱式气体绝缘母线中三相导电杆的换热系数不能按统一公式进行计算。传统的圆筒形物体的换热系数可以通过根据经验公式进行求解的，但目前并没有关于封闭空间中多热源的对流换热系数的经验公式，所以如表2所示。

表2 负荷电流-对流换热系数关系式系数Tab.2 Relationship coefficient of load current-convective heat transfer

选用有限元数值方法计算求得二维流体场参数中的对流换热系数，对三相共箱式绝缘母线A、B、C三相母线和外壳的对流换热系数与负荷进行一次多项式拟合，得到负荷电流-对流换热系数的经验数学关系表达式：

对三相共箱式绝缘母线A、B、C三相母线和外壳的对流换热系数与温升（见表3），进行三次多项式拟合，得到温升-对流换热系数的经验数学关系表达式：

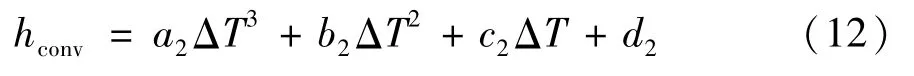
表3 温升-对流换热系数关系式系数Tab.3 Relationship coefficient of temperature rise-convective heat transfer

3.2 辐射换热系数的计算

辐射换热的定义中不涉及流体的变化，仅于固体空间位置、大小有关，则三相共箱式气体绝缘母线的辐射换热量易于求解得到。两导体的辐射量采用角系数表述，角系数表示为导体表面1对导体表面2的投射辐射量占导体表面1的有效辐射的比值。导体间的辐射的角系数的计算公式表示为：

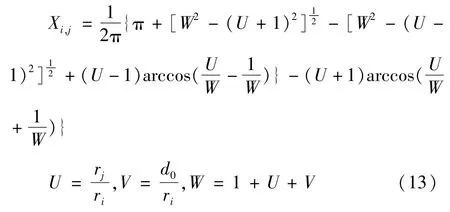
式中 ri，rj分别为两导体半径。

为了计算三相共箱式气体绝缘母线灰色系统的辐射传热量的计算式，需引入有效辐射J，其包括自身辐射E以及投射辐射中被表面反射的部分ρG。有效辐射J与表面净辐射换热量q之间的关系为：

气体绝缘母线的导体与外壳之间的辐射换热系数求解式为：

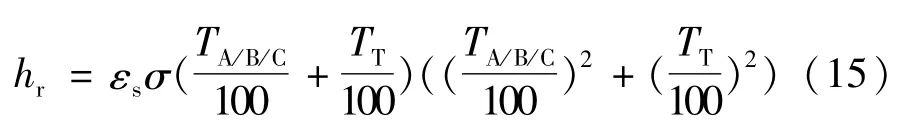
其中：

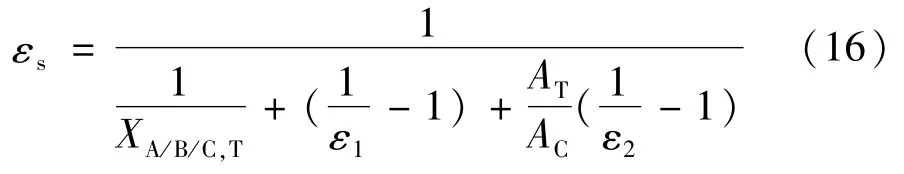
式中 ε1为导体外表面发射率，取值为0.6；ε2为外壳内表面发射率，取值为0.8；XA/B/C，T为三相导体分别与外壳间的辐射角系数值；σ则取为5.67 W/（m2·K4）；AT为外壳内表面的计算面积；AC为导体外表面的计算面积。

3.3 热阻的计算

根据辐射换热系数以及对流换热系数的求解，根据式（17）可分别求出辐射换热热阻以及对流换热热阻：

式中 Ad为组件的等效对流/辐射散热面积，m2；hd为组件的自然对流换热系数，W/（m2·K）；hr为组件的辐射换热系数，W/（m2·K）。

三相导体与SF6气体之间的热阻是由导体的对流换热热阻和辐射换热热阻并联构成：

外壳与SF6气体之间的热阻只考虑对流换热热阻，则有：

3.4 气体绝缘母线外壳对环境的参数计算

气体绝缘母线外壳与周围环境之间的热量传递是一种复合换热过程，即辐射换热和自然对流换热。气体绝缘母线外壳表面总散热量q总等于辐射换热q1和自然对流换热q2之和，即：

（1）气体绝缘母线外壳对环境的辐射换热

根据斯忒潘-玻尔兹曼定律，外壳对周围环境的辐射换热量为：

式中 ε为外壳表面发射率，取0.8；A1为外壳单位长度的散热面积，m2，A1=πD，D为外壳的外径，m；Tt、Ta分比为外壳和周围环境的绝对温度，K。

（2）气体绝缘母线外壳对环境的自然对流换热

由传热学原理有：

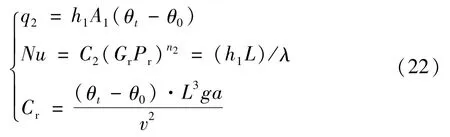
式中 h1为空气的自然对流传热系数，W/（m2·K）；L为外壳表面对流散热面积，取 L=1 m；λ、α、ν、Nu、Gr、Pr为空气的热物理参数。

结合式（10）和空气的物性参数计算可知107＜Gr＜1012，查阅相关文献可知［16］，C2=0.125，n2=0.333。将式（21），式（22）代入式（20）得：

3.5 热容与时间常数的计算

根据传热学原理，在进行非稳态分析时，一般以热时间常数反映母线温度变化的快慢程度。热时间常数是指在非稳态导热过程中温升由零达到最大温度变化幅度的63.2%时所需的时间，其计算公式为：

式中τ为热时间常数；Rx、Cx分别为GIS母线各组件的热阻和热容。

根据热容的定义［17］有：

式中c、m分别为母线各组件的比热容与质量。

4 热路模型计算值与实测值的对比

气体绝缘母线的载流能力大小是对其整个导电回路载流能力的整体评价，母线任何一个部分的过热均会导致其整体载流能力的下降，因此，气体绝缘母线温升是衡量气体绝缘母线安全运行水平的重要标准。为了验证论文前述气体绝缘母线温升数值计算模型的正确性，同时研究母线触头温度与外壳表面温度之间的对应关系，进行了气体绝缘母线原型物理模型的温升实验。实验平台如图3所示。

图3 母线原型温升实验平台Fig.3 Temperature rise experimental platform of the GIB prototype

运用Runge-Kutta法求解方程组（9），把计算结果和试验结果进行比较分析。接触电阻为14μΩ，环境温度为25℃，热路模型的计算步长为15 min。额定电流下的三相共箱式气体绝缘母线温升特性如图4所示。

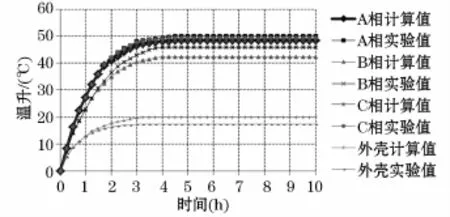
图4 额定负荷电流下母线各组件温升特性Fig.4 Temperature of the GIB under different rated load currents

32.5℃恒定的环境温度，负荷电流分别为0.6 kA、1 kA、1.2 kA、1.5 kA以及2 kA时气体绝缘母线三相导体与外壳稳态温度值如图5所示。

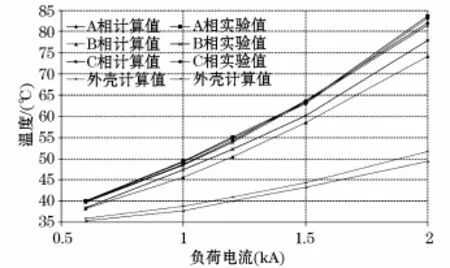
图5 不同负荷电流下母线各组件温度Fig.5 Temperature of the GIB under different load currents

由图4和图5中的对比结果可以看出，在实验电流范围内，三相共箱式气体绝缘母线温度的计算值与实测值均吻合较好，原型物理模型温升实验验证了三相共箱式气体绝缘母线热路模型的正确性、合理性及有效性。

为研究环境温度、负荷电流及接触电阻综合作用条件下气体绝缘母线导体与外壳温升之间的对应关系，以外壳温升作为监测状态量，能降低环境温度变化对温度测量结果的影响，外壳与导体对应温升曲线如图6所示。

由图6可见，A、B、C三相导体温升与外壳温升呈近似线性关系，在外壳温升相同情况下，A、C两相导体的温升比B相导体温升值高，即A、C触头温升变化率比B相导体大；随着外壳温升的逐渐增加，A、C两相导体与B相导体温差越来越大。根据上述规律，对三相共箱式气体绝缘母线三相导体温升进行线性拟合，三相共箱式气体绝缘母线的外壳温升-导体温升的数学关系式表示为：

图6 外壳与导体温升对应曲线Tab.6 Temperature rise corresponding curve of shell and conductor

式中ΔθC、ΔθT分别为母线导体温升值以及外壳温升值；a、b为多项式系数。系数取值如表4所示。

表4 系数取值表Tab.4 Table of coefficient value

5 结束语

根据传热学基本原理，考虑了SF6气体温度变化对母线导体温度的动态影响，同时考虑了外壳与周围环境之间的热交换、导体和外壳换热系数、母线导体热容以及导体和外壳分别与SF6气体之间的非线性热阻对气体绝缘母线温度变化的影响，建立了正常运行条件下气体绝缘母线的动态等效热路模型，并设计了三相气体绝缘母线温度测量试验，将模型计算结果与试验结果进行对比分析。分析结果表明，解析法与试验结果的相对误差均小于5%，满足工程应用的要求，表明了所建气体绝缘母线动态热路模型的准确性和有效性，并通过所建立的热路模型得到了外壳与导体对应温升曲线。