基于Hopf分岔的电力系统HVDC稳定直流分段控制策略

任民

（安徽省电力公司电力科学研究院计量中心，合肥230088）

0 引 言

HVDC技术可用于解决大量存在的交流电力系统的稳态以及动态不稳定问题。在交流电网的HVDC线路整合中有三种主要方法［1-3］：HVDC电网与交流输电网结合；在交流电网的交流母线之间嵌入HVDC线路；直流分割。直流分割作为文章研究重点，是指一个大的交流电网通过HVDC线路连接分解成更小的段连接。由HVDC线路构成各电网段的主电源传输通道。

虽然已经有关于直流分割的交流电网研究，但并未对其在提高电力系统稳定性方面进行充分的调查和量化。文章的重点是确定直流分段交流系统的最佳工作点，以提高稳定裕度和改善的交流段的振荡模式的阻尼。文献［4-13］讨论各种工作点的调整策略，以提高稳定裕度，降低电力系统的低频振荡。其中，文献［4-5］基于同步电机的电压控制，文献［6-8］基于无功功率控制，文献［9-11］基于有功功率控制，文献［12-13］稳定约束研究传统最优潮流（OPF）问题的Hopf分岔现象。但是上述策略中均未使用HVDC设定值调整实现稳定性改进。

1 相关工作

基于无功功率控制方法，需要用到可控的无功功率器件，这是难以实现的。基于有功功率控制方法难以进行实际应用，因为大多数发电机不能进行自动发电控制（AGC），可能需要花费几分钟的时间来回应和再发送指令。此外，文献［5，9-11］需要正负敏感性，这对于确保有功和无功功率平衡并不充分。

图1给出每种方案进行电网平衡和频率调节的持续时间。主控制发生在干扰产生后几秒以内，二级控制部署在分钟时间框架内，依靠电力供应商进行直接控制（发电机和负荷调度）。次级控制的最常见类型是通过AGC进行控制。对于不在AGC的发电机组，三级控制用来重新调度发电机组和改变系统工作点。与三级控制的直接调整发电机（从几分钟内到几小时内）不同，这里提出HVDC设定值快速调整策略通过其主控制器直接进行发电机调度。由于该方法通过主控制器进行调度，因此其控制时间大幅缩短，可在秒级时间框架内完成。与交流线路相比，HVDC链路的功率流的可控性较高，可用来调整直流分段交流系统的工作点，移动临界特征值的实部进一步远离虚轴，因此，可增加振荡模式的稳定裕度和阻尼比。文章研究重点是确定HVDC线路的最佳设定点，从而获得稳定裕度较高的Hopf点和高阻尼比。Hopf分岔理论用来控制HVDC线路的功率流，实现系统操作点的改变。

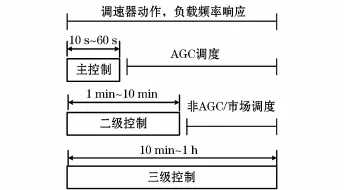
图1 电网平衡和频率调节的控制连续性Fig.1 Control continuity of power balance and frequency control

改变直流有源功率设定值，可间接地实现发电机的有功功率和无功功率输出调度。与以前依靠发电机直接控制的方法进行对比，该方法可对实时事件做出更迅速的反应，如线路中断，因为发电机自动调整是基于有功和无功功率进行控制器设计。文献研究表明最佳HVDC设定值可用于：系统故障的暂态稳定；鲁棒性故障和负载因子的变化的预测控制。

2 研究背景

2.1 系统模型描述

这里研究对象有两个：2段系统和3段系统，与2段系统相比，3段系统更具有一般性。尽管如此，在为更好的阐述所提算法的优越性，仍然考虑将2段列入研究对象。其中，2段系统是由两个相同的系统片段构成，每个系统均为一个IEEE14总线系统，而3段系统是由三个相同的IEEE14总线系统构成。

在2段系统中，两个相同的系统段通过两个HVDC整流器连接：HVDC1和 HVDC2。同理，在3段系统中，三个相同的系统段通过三个HVDC整流器连接：HVDC1、HVDC2和HVDC3。虽然交流子系统的配置相同，但是因为连接的高压直流输电线路的连接点和每段高压直流输电线路的注入和吸收功率不同，导致子系统呈现不同的电力特性，并表现出不同的振荡模式。

研究中，交流系统包括涡轮发电机（T-G）机组及其控制器，交流输电线路和变压器。机电一体化系统由圆形转子磁场同步控制电机（SM）和涡轮系统构成。每个SM的电气系统表示为四阶系统，包括励磁绕组、转子-轴阻尼绕组以及转子-轴双阻尼绕组。这里假定SM的磁回路是线性的。每个T-G机组配备有一个IEEE I型激振器和一个TGOV1调速器。T-G机组旋转机械系统是由一个单一的刚体模型构成。由变压器和交流输电线路组成的交流输电网络是基于网络节点方程的正序代数方程。文献［6］利用注入建模方法进行高压直流输电系统表示。各换流站表示为对应换流变压器电抗的等效电源；因此，高压直流输电线路的HVDC链路模型只对代数方程产生影响。

2.2 系统代数方程

将介绍交流系统代数方程的HVDC系统模型集成方法。令g（x，y，λ）=0表示SMs的定子电路的代数方程组见式（1），网络节点方程见式（2），坐标变换方程见式（3），以及高压直流输电系统代数方程组见式（4）。

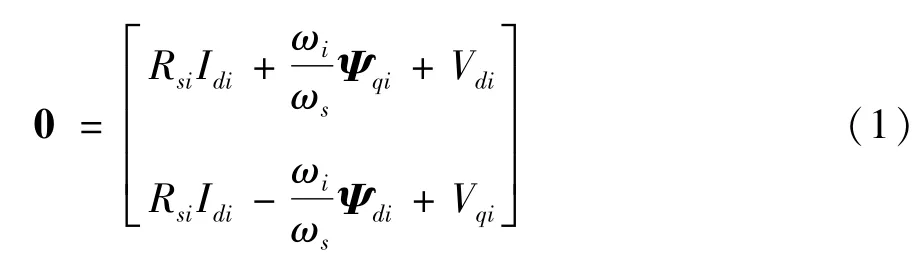
网络节点代数方程表示交流输电网络，形式为：

坐标变换的代数方程组为：

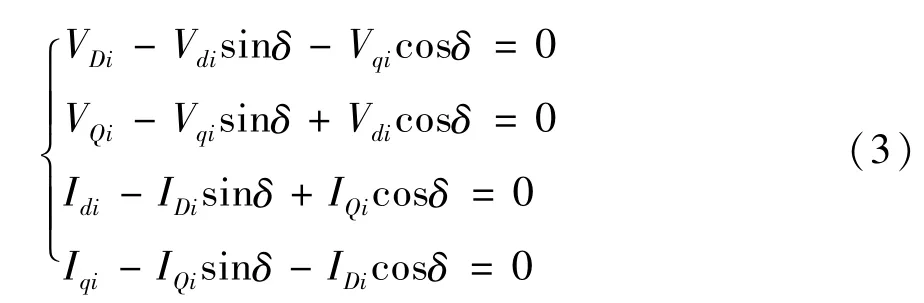
所有HVDC总线的直流线性代数方程组为：

多机交直流系统的向量微分代数方程为：

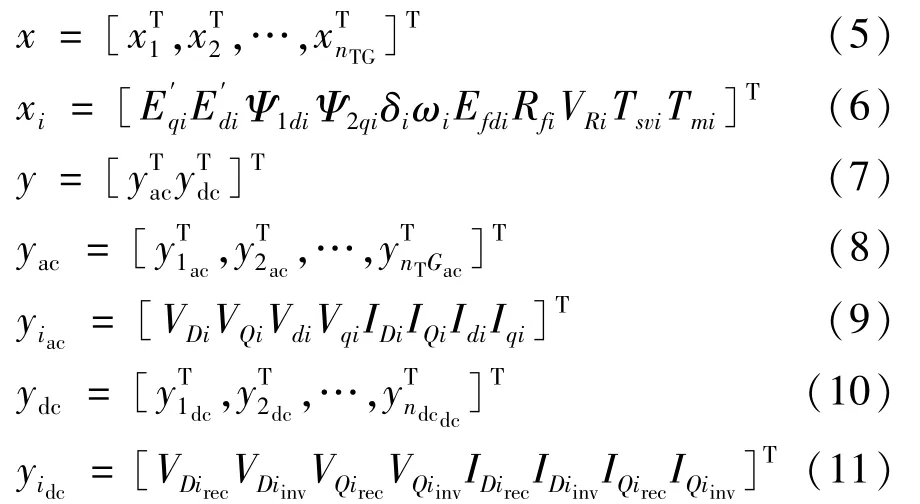
3 Hopf分岔点雅可比灵敏度计算

所研究的电力系统模型形式如下：

式中 x∈Rnx，y∈Rny和λ∈Rm分别是动态状态变量、代数变量和参数向量。˙x=f（x，y，λ）和0=g（x，y，λ）分别代表微分和代数方程，其中：

式（12）中，通过 F=［fT，gT］T，F∶Rnz+m→Rnz，nz=nx+ny，z=［xT，yT］T，F（z0，λ0）=0可定义系统的平衡点（z0，λ0）。

当参数小变化会导致系统的行为突然改变时，就会产生分岔现象。基于系统的动态流形和平衡点，分岔现象可以是局部的或全局的。文 中主要研究局部分岔问题，特别是Hopf分岔问题，可以基于线性系统状态矩阵的特征值进行确定：

式中 fx是f对于x的雅可比矩阵；fy是f对于y的雅可比矩阵；gx是g对于x的雅可比矩阵；gy是g对于y的雅可比矩阵。直接计算Fx的特征值需要进行gy矩阵求逆操作，这会导致稀疏性破坏。为保留稀疏性，直接采用式（12）的雅克比方法解决“广义”特征值问题，并确定的Fx特征值Λ和特征向量e1，形式如下：

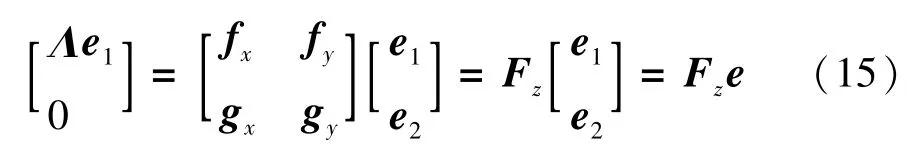
式中 Fz为 F对于z的雅可比矩阵。根据式（15）获得的Fz的广义特征值，相当于系统状态矩阵Fx的特征值。对于Hopf分岔现象，F的复数特征值随着系统参数的逐渐变化，逐渐穿越复平面。系统参数向量λ=［μ，p］为不可控参数μ，例如系统负荷，以及一组可控参数p，例如HVDC设定点值。当不可控参数沿应力方向μ0在固定可控参数p0情况下增加，当复特征值实部为0时，系统到达不可控制参数值μ*2的Hopf分岔点，此时该系统不再是小信号稳定的。稳定裕度可定义为：

式中Fλ为F对于λ的雅可比矩阵。M相对于参数p的灵敏度是一个普通向量相对于∑Hopf的缩放投影。∑Hopf的法向量可通过对参数本征值的实部敏感性进行确定：

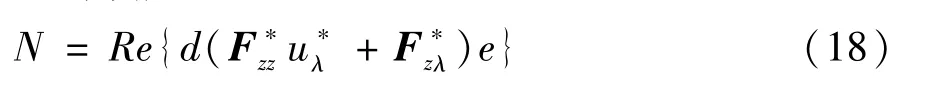
式中 Fzz为 nz×nz×nz张量，是 F相对于 z的Hessian矩阵，Fzλ为nz×nz×m的张量，是F相对于z和λ的Hessian矩阵。d和e为Fz相对于jω*的归一化的右和左特征向量，满足de=1和|d|=1。d和e可通过求解广义特征值进行确定，此外，如果：

那么：

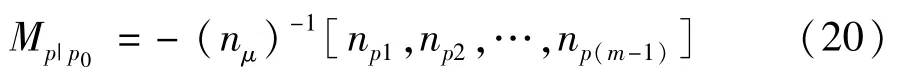
式中Mp|p0即为考虑控制参数的敏感性稳定裕度。

4 优化计算过程

本研究目的是控制图2和图3所示HVDC输电链路有源功率流，从而提高2段和3段电力系统的稳定裕度。因此，将HVDC线路的有功功率设定值p作为控制参数。因为Mp|p0是N的缩放投影，运动方向远离Hopf曲面意味着稳定裕度和振荡模式阻尼比的增加。在优化过程中，阻尼比计算相对于稳定裕度更为简单，同时增加阻尼比会倾向于增加稳定裕度。因此，为了提高稳定裕度，目标是最大限度地提高阻尼比的最小阻尼模式。

为获得HVDC系统的最佳工作点（最高阻尼比），可对以下问题进行求解：

其中：

式中PDC和nmode分别是直流连接的有源功率向量和振荡模式的数量。其目标是要确定获取最小阻尼振荡模式的最大阻尼比的直流连接有功功率设定值。在约束式（22）中，前两个约束是确保系统处于稳态，第三个约束是对直流母线注入功率进行限制。优化过程步骤如图2所示。

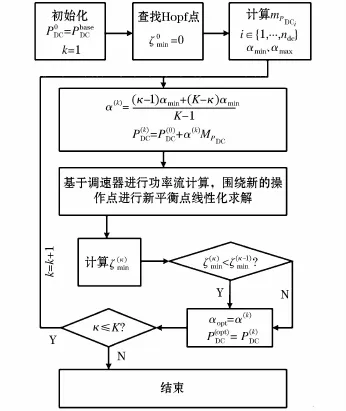
图2 优化流程图Fig.2 Flow chart of optimization

然后对［αmin，αmax］中的K个等间隔点进行测试。在线路搜索过程中，基于调速器的功率流（GBPF），求解每次更新后的直流值。在（GBPF）问题中：（1）每段的净直流负载，定义为从相邻的段注入和吸收的直流电源之间的差异，该值是确定的；（2）从初始解的净直流负载变化进行计算；（3）在每一段，在每个发电单元的输出变化可由其下降特性测定。基于工作点的径向基函数对系统模型进行线性化，然后用来计算振荡的阻尼比模式，并对目标函数（21）进行评估。

5 实验分析

在这一部分中，基于Matlab/Simulink仿真环境对两个案例进行研究。本算法得到的每个测试系统在最佳工作点的稳定裕度和特征值与传统方法获得的成本最小化的优化解决方案进行对比。此后，无任何约束的传统优化解决方案，作为本算法的基础解决方案。

5.1 案例1：2段系统研究

假定HVDC线路是无损的，即Prec=-Pinv；因此，只有2个可控参数，PDC1和PDC2，取值范围是［-1，1］。在系统中所有负载相对于基准值的变化为：

式中β是负载因子。对HVDC线路的有功功率初始设定值为PDC1=-0.90 p.u，PDC2=-0.74 p.u。在初始工作点，所有具有负实部特征值的系统都是稳定的。当β由0到0.997 5变化时，该2段系统的Hopf分岔点为β*=0.997 5。

图3显示了在β*=0.997 5时，与振荡模式相关联的系统特征值的频率小于2 Hz，而阻尼比小于0.5。当系统运行在传统OPF方案时，该系统是Hopf分岔的。然而，在HVDC设定值进行调整时，最接近虚轴的振动特征值的实部为-1.1，稳定性上要优于传统OPF方案。

图3 两操作点的系统特征值对比Fig.3 Comparison of the system eigenvalues of two operating points

图4给出了发电成本增加和阻尼比增加之间的权衡过程。上图显示出随α变化的最接近虚轴的振荡特征值实数部分。下图显示从优化问题得到解决方案，可导致振荡模式阻尼比的增加，αopt=0.17。然而，阻尼增加会伴随着发电成本增加，αopt选取需要根据实际情况决定。

图4 发电成本及参数σ与优化步长Fig.4 Cost of power generation and the parameters and the optimal step size

5.2 案例2：3段系统研究

本案例研究中的可控参数位：PDC1、PDC2和PDC3。由于负载变化导致系统产生 Hopf分岔现象。在Hopf分岔点，利用可控参数对临界特征值的实部灵敏度进行计算，并利用灵敏度信息，调整HVDC直流远离虚轴特征值。

图5所示为与α相关的最接近虚轴的振荡特征值的实部随阻尼比σ的变化情况，其呈现出先降低后增加的现象，也就是αopt=0.02是算法稳定性最好的步长值。

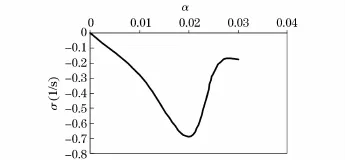
图5 参数σ随最优步长变化Fig.5 Parameter changes with the optimal step size

图6显示了阻尼比小于0.3及频率小于2 Hz的振动模式相关联的系统特征值。当系统运行在最优潮流的解决方案（OPF）时，所有的特征值均位于虚轴的左侧。当负载增加时，特征值移向虚轴直到系统发生Hopf分岔。而直流设定值调整（HVDC），振荡模式远离虚轴，并且振荡模式的阻尼比增加。

为验证特征值分析的结果，这里同时也给出时域仿真结果。图7给出3段系统片段3的T-G单元有功功率偏差结果，故障发生在片段3的总线14处，在0.5 s时产生0.6 s时消失。在故障发生之前，该系统工作在传统OPF方案下，并且处于Hopf分岔状态。

图6 三操作点的系统特征值对比Fig.6 Comparison of the system eigenvalues of three operating points

图7表明，当直流设定值进行调整后（故障被清除后），振荡动力学阻尼比调整和稳定速度要快于OPF方案，控制稳定时间小于5 s，而根据实际的实验数据，后者震荡时间超过20 s。这体现了本文所提方法的快速控制优势。

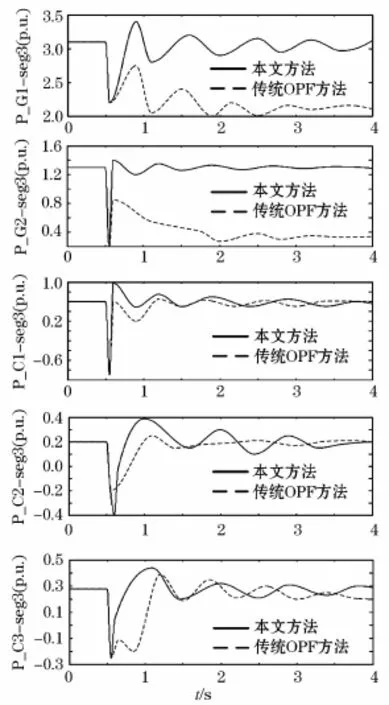
图7 片段3发电机组有功功率偏差Fig.7 Deviation of the active power of the 3-fragment generating set

表1给出在最佳工作点的发电机输出的变化，以补偿HVDC上的功率流变化。因为在最佳工作点，可通过HVDC的连接2和3对片段3进行功率注入，以降低片段3的T-G单元发电量。同时由于由片段2向片段3注入功率，会导致片段2的T-G单元发电量增加，同时也导致片段1的T-G单元发电量略微增加。

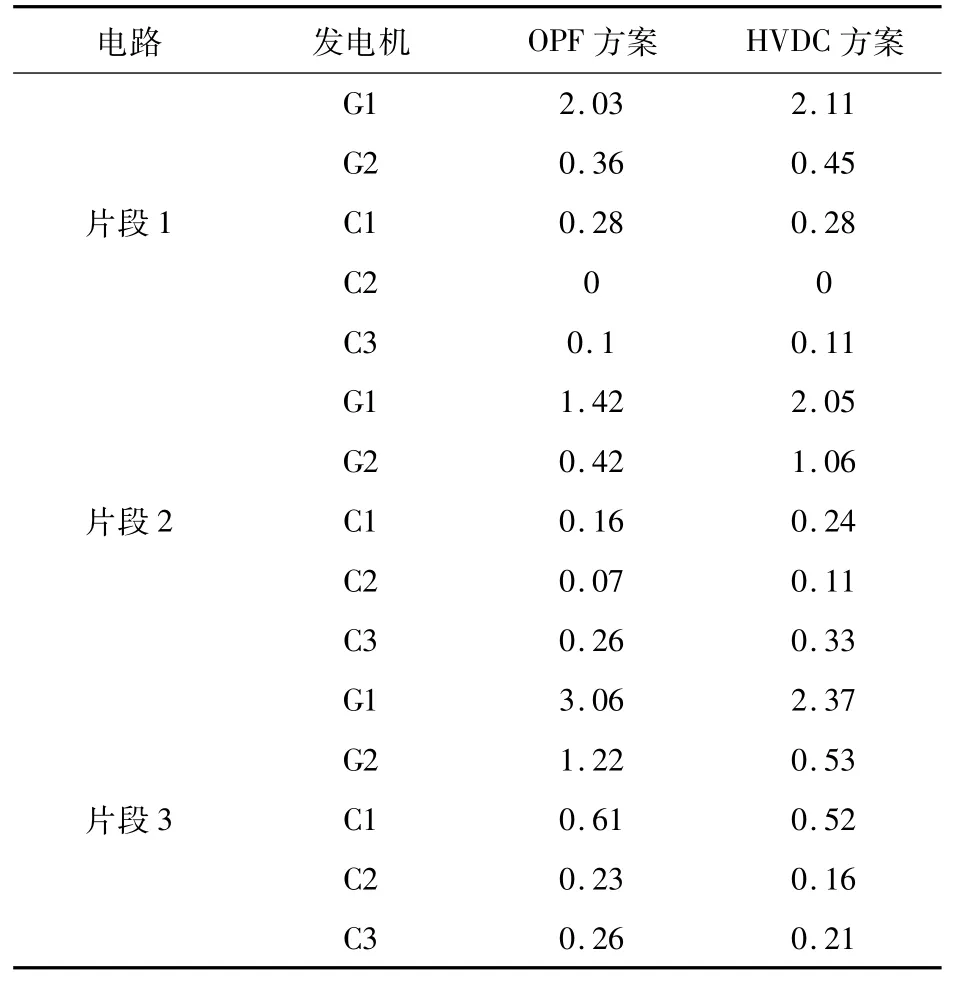
表1 系统T-G单元发电量Tab.1 Generation capacity of system T-G unit

6 结束语

提出一种电力系统直流分段Hopf分岔雅可比灵敏度HVDC稳定控制策略，可快速解决电力系统的动态不稳定问题。该策略基于Hopf分岔点雅可比灵敏度，采取HVDC线路工作点调整策略。通过在2段和3段系统的实验结果显示所提算法具有较高的控制精度和快速的控制速度。