基于时变安全距离的跟驰模型反馈控制*
翟聪 巫威眺 黄玲 刘伟铭 郑丽媛
(1. 华南理工大学 土木交通学院, 广东 广州 510640
2. 佛山科学技术学院 交通与土木建筑学院, 广东 佛山 528000)
基于时变安全距离的跟驰模型反馈控制*
翟聪1,2巫威眺1†黄玲1刘伟铭1郑丽媛1
(1. 华南理工大学 土木交通学院, 广东 广州 510640
2. 佛山科学技术学院 交通与土木建筑学院, 广东 佛山 528000)
为了更真实地反映交通流特性,在Konishi提出的耦合映射(CM)跟驰模型基础上,考虑不同速度下车辆的不同安全距离,设计了新的安全距离表达式,随后提出了一类基于时变安全距离的CM跟驰模型,并对模型的稳定性进行了研究;基于稳定性理论,给出了模型满足稳定和交通拥挤现象不会出现的充要条件,在此基础上设计了一类滞后反馈控制器以更好地抑制交通拥堵;最后通过仿真算例,对比了Konishi模型和新跟驰模型在抑制交通拥堵和车辆行驶过程中二氧化碳排放方面的性能.仿真算例表明:与Konishi跟驰模型相比,基于时变安全距离的跟驰模型的收敛性更强;所设计的控制器能通过调整车队速度有效缓解交通拥堵和降低车辆二氧化碳排放.
CM跟驰模型;时变安全距离;稳定性;滞后反馈控制器;二氧化碳排放
随着机动化水平和城市化水平的提升,越来越多的交通问题也随之产生.为了缓解交通问题,一方面,学者们提出了一系列交通需求管理策略引导出行行为,如拥挤收费策略等;另一方面,有学者从车流运行演化角度探索交通拥挤形成机理,并提出了各类交通流模型,包括跟驰模型[1]、元胞自动机模型[2]、水动力模型[3]等.传统的跟驰模型和水动力模型利用微分方程或者偏微分方程建立交通流的具体表达形式,然而,当考虑的因素较多时,模型的复杂程度会呈指数增长,因而不利于仿真和求解.元胞自动机模型则利用一系列交通规则更新交通状态,有效降低了模拟计算的复杂度,但是此类模型仅能够初略再现特定现象,很难分析现象的形成机理,因此,整合这两类模型的优势显得很有意义.
了解决上述问题,Yukawa等[4- 5]利用耦合映射理论对传统的跟驰模型进行离散化处理,提出了耦合映射跟驰模型,与以往模型相比,该模型具有结构简单、易于分析仿真的特点.至此之后,学者们运用耦合映射跟驰模型从不同角度对交通问题进行分析,比较有代表性的有:Konishi[6]在Bando提出的最优速度函数基础上,对不允许超车的单车道耦合映射跟驰模型的稳定性问题进行研究;Zhai等[7- 9]考虑驾驶员的时变滞后反应时间,从驾驶员特性角度建立了时变滞后耦合映射跟驰模型,并对模型的稳定性问题进行了探讨;Huang等[10]分析了车间通讯对车流运行稳定性的影响;葛红霞等[11]提出了优化速度函数中涉及前方两辆车车头间距的耦合映射跟驰模型;韩祥临等[12]考虑智能交通诱导提供的前
车信息,对耦合映射跟驰模型进行改进;Han等[13]提出了一种驾驶员带有非恒定灵敏度的耦合映射跟驰模型;Fang等[14]探讨了耦合映射跟驰模型的混沌问题;其余的相关文献可参考文献[15- 16].另有一些文献在分析车辆跟驰行为的基础上研究消除拥挤现象的方法.例如,孙棣华等[17]从融合交通信息系统和交通物理系统的角度,运用反馈控制理论,提出了考虑最邻近前车综合信息的交通拥堵反馈控制方案;Zhao等[18]在Konishi的基础上,设计了含滞后项的反馈控制器,发现在抑制交通拥挤方面更加有效;Fang等[19]考虑相邻车辆速度差对车流稳定性的影响,设计了静态和动态的反馈控制项以抑制交通拥挤现象.
尽管目前有较多耦合映射跟驰模型的研究成果,但是仍然存在着一些局限性.在安全管控方面,以往的模型均假设每辆车的安全距离是恒定的,而这一假设与实际车辆安全距离分布情况明显不符.通过驾驶模拟发现,车辆安全距离在不同行驶状态下是有所差异的[20].另外,当车辆的制动加速度恒定时,为保证车辆不发生碰撞,车速较高的车辆比低速行驶的车辆需要更大的安全距离,因此,车辆的安全距离和车辆的行驶速度(制动速度)呈现正相关的关系.制动距离在道路设计与运行管理中是控制视距的一项重要指标,道路上高速行驶的车辆在遇到突发事件需要紧急制动时因车辆制动距离过长和车辆制动不稳定而发生的事故频发,因此,有必要从安全管控角度研究车辆跟驰模型,并依此设计车队运行控制机制,为交通安全管理提供理论基础.
有鉴于此,文中提出一种时变安全距离的耦合映射跟驰模型,在构造安全距离与速度关系表达式的基础上,对该模型的稳定性进行分析.为了抑制交通拥堵,本研究设计了时滞的反馈控制器,同时给出了控制器的具体形式,最后通过仿真算例对该方法在缓解交通拥堵和降低废气排放方面的有效性进行了验证.
1 模型建立
N辆车行驶在单车道上时的模型如图1所示.
为了研究单车道的车辆跟驰行为,根据Konishi提出的CM跟驰模型,文中假设头车匀速运动,则头车的运动轨迹可通过下式给出:x0(n+1)=v0T+x0(n)
(1)
其中,x0(n)表示头车在t=nT时刻的位置,v0(v0>0)表示头车的速度,T代表采样时间.与此类似,后续跟驰车辆的运行轨迹可表示为
xi(n+1)=vi(n)T+xi(n)
(2)
(i=1,2,…,N)
其中,xi(n)表示第i辆车在t=nT时刻的位置,N表示总的车辆数,vi(n)>0代表第i辆车在t=nT时刻的瞬时速度,其中vi(n)可通过如下表达式得到:

(3)

为了保证方法的可比性,文中仍沿用文献[8]提出的最优速度函数:
(4)
其中饱和函数Hsat(·)为

在以往研究中,安全车间距ηi设为恒定值,而该假设明显不符合实际情况,根据上述讨论,车辆制动距离与行驶速度呈正相关关系.为了充分反映该特性,文中提出如下车辆安全距离表达式:
ηi(n)=ηlim+βvi(n)T
(5)

基于此,文中提出带时变安全距离的CM跟驰模型,表达如下:
(6)

图1 N辆车行驶在单车道上时的模型Fig.1 A platoon of N cars running on a single lane
当β=0时,式(6)所示模型可转化为文献[8]所提出的CM跟驰模型,所以文献[8]的CM跟驰模型是文中模型的一个特例.
2 稳定性分析
考虑前车(i-1)以速度v0匀速行驶,则车辆i的动态方程可表示为

(7)
式(7)所示系统的平衡状态为
(8)



(9)
式(9)所示系统的特征多项式为
Pi(z)=z2+aiz+bi
(10)
其中,ai=αiT+βαiriT2-2,bi=1-αiT+(1-β)αiriT2.
基于Jury准则,可得到式(9)所示系统满足稳定的充要条件.
定理1 当下列条件
(11)
成立时,式(9)所示系统是稳定的.
证明根据Jury稳定性判据,系统(9)满足稳定的充要条件为
{Pi(1)>0
Pi(-1)>0
|Pi(0)|<1
(12)
当不等式(11)满足时,式(12)同样满足条件,证毕.
当前车(i-1)遭受外部干扰无法以恒定速度v0匀速行驶时,则车辆i的误差方程可表示为
(13)
则关于δvi-1(n)到δvi(n)的转移函数可表示为


(14)
其中,Pi(z)=z2+aiz+bi.
根据交通流系统原理可知,当Pi(z)满足稳定,且‖Gi(z)‖∞≤1时,则可知交通拥挤现象将不会出现.
定理2 当车队中所有车辆运行的参数满足如下不等式时:
(1)如果1-αiT+(1-β)αiriT2>0
(15)
(2)如果1-αiT+(1-β)αiriT2<0
(16)
则交通拥挤现象不会出现.
证明通过定理1可知,当满足式(11)时,系统(9)满足稳定性,下面仅验证当不等式(15)和(16)满足时,能够满足‖Gi(z)‖∞≤1.
首先,状态转移函数的绝对值‖Gi(z)‖可利用下式进行表述:

(17)


(18)
其中:

则原问题‖Gi(z)‖∞≤1可转化为

(19)
根据式(15)和(16),可知下列条件
成立,则条件(19)成立.
从以上可知,当交通流系统满足定理2时,该系统具有一定的鲁棒性,也即当车辆遭受一定的外部干扰时,车队能够通过自身速度调节,最终回到平衡状态,即交通拥挤现象不会出现;当外部干扰增加到一定程度时,车辆运行参数可能不再满足定理2,此时交通拥挤将再次出现,下面将通过设计控制器抑制外部干扰和交通拥挤.
3 反馈控制器设计
为了抑制交通拥挤问题,基于当前车辆与上一时刻瞬时速度差信息,文中提出新的反馈控制器,在式(6)中加入速度控制项ui(n).
(20)
其中,ui(n)的具体的形式如下:

(21)

则关于δvi-1(n)到δvi(n)的转移函数可表示为
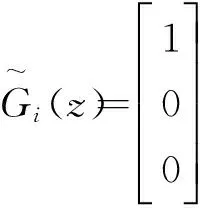

(23)
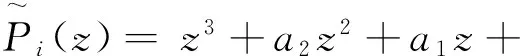
与定理2相似,为了抑制交通拥挤,式(6)所示模型在反馈控制器ui(n)作用下应满足:


定理3 若式(6)所示模型在式(21)所示反馈控制器作用下满足如下条件:
(24)

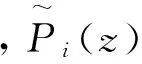
(25)
(26)

4 二氧化碳排放模型
二氧化碳的过量排放直接影响着人们的正常生活,环境调查报告中指出,目前全球二氧化碳排放总量的40%来源于汽车尾气.为了降低汽车尾气排放,众多学者从不同角度提出了排放模型[21- 22].与文献[9]类似,文中引入排放模型来评价实施控制器的效果,在此沿用文献[23]中提出的排放模型,该模型可表述为:
(27)
(28)

5 仿真算例
本节通过数值算例验证文中所提出方法的可行性和有效性.假设有50辆车行驶在开放边界的单车道上,且车与车之间不允许有超车行为,头车以速度v0=20 m/s匀速行驶,车辆的最大行驶速度vmax=33.6 m/s,碰撞间距ymin=7.02 m,最短安全间距ηlim=20 m,调节系数ζ=23.3,采样时间T=0.1 s,为了研究方便,假设每名驾驶员是同质的,即ai=2 s-1,i=1,2,…,50,下面给定每辆车的初始位置和速度,其中:
vi(0)=v*=20 m/s,i=1,2…,50.
当头车在时间段[100 s,102 s]内突然受外部扰动影响,需要停车,即
100 s≤nT≤102 sx0(n)=0.
下面通过展示在控制器作用前后的速度-时间图及车间距-时间图,对比Konishi提出的经典CM跟驰模型和文中提出的时变安全距离CM跟驰模型的性能.
两种跟驰模型在无控制器作用下车辆的车间距变化情况如图2(a)、2(b)所示,可以看出,在Koni-shi模型中,当头车遭受外部干扰时,车辆间的相互作用加强,使得车辆加减速频繁,且车辆间的相互作用迅速向后传递,引起车队整体运行的巨大波动,因而该模型易发生交通拥堵;相比之下,时变安全距离跟驰模型的拥挤持续时间更短,从而可知,文中模型的收敛性更强.两种模型在加入反馈控制器后的运行特性如图2(c)、2(d)所示,,通过求解定理3,获得控制器的增益项k=0.4,对比图2(c)、2(d)不难发现,相比较于图2(a)、2(b),Konishi模型在控制器作用下,车队整体趋于稳定,车辆间的相互作用较低,但是仍然存在着一定的干扰,而图2(d)与图2(c)相比,车辆间的相互影响得到了进一步的减弱,虽然未根本消除车辆间的干扰,但是该影响已经可以近似忽略.
图3、图4给出了Konishi耦合映射跟驰模型和时变安全距离跟驰模型在控制器作用前后的车辆速度-时间图,其中图3仅对其中的第1、25、50辆车的速度进行分析,而图4中对所有车辆进行描述.
从图3(a)、3(b)不难发现,在Konishi模型中,越靠近车尾位置的车辆速度震荡幅度越大,同时其震荡时间也越长,车队也越难以恢复到平衡状态;相比于图3(b),在新CM跟驰模型中,除了头车的震荡,编号为25和50的车辆震荡时间和幅度均大幅度减少,说明文中模型的车队运行整体收敛性较强,车辆可以在较短的时间内重新恢复到平衡状态.通过图3(c)、3(d)可知,在控制器作用下,编号为25和50的车辆的速度震荡幅度得到了进一步的降低,即新CM模型在定理3所设计的控制器作用下交通拥堵发生的概率最低,通过图4中所有车辆的速度随时间的变化曲线可以验证这一点.综合图2-4可以知道,文中所设计的时变安全距离的CM跟驰模型相比于Konishi跟驰模型车辆的收敛性得到了增强,同时新模型在文中所设计的控制器下在抑制交通拥堵方法中效果更好.




图2 车间距-时间图Fig.2 Headway-time curves of all cars


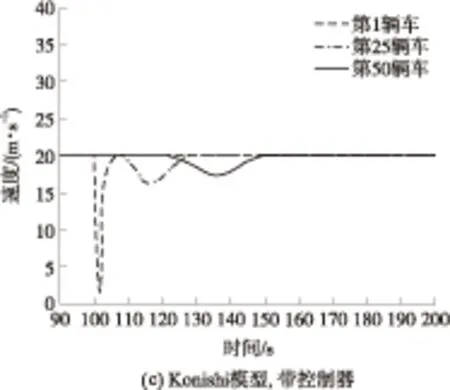

图3 第1、25、50辆车的速度-时间图


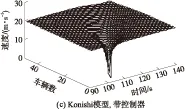

图4 所有车辆的速度-时间图Fig.4 Velocity-time curves of all cars
最后,文中验证该控制器在降低车辆行驶过程中废气排放方面的有效性.其中Konishi耦合映射跟驰模型和时变安全距离跟驰模型在控制器作用前后的二氧化碳排放-时间曲线如图5、图6所示,其中图5仅对其中的第1、25、50辆车的速度进行分析,而图6中对所有车辆进行描述.




图5 第1、25、50辆车的二氧化碳排放量-时间图
Fig.5 Carbon dioxide emission-time curves of the 1th,25th,50thcar

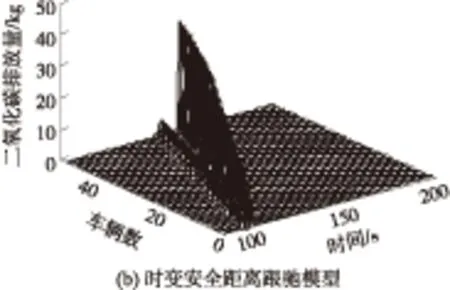


图6 所有车辆的二氧化碳排放量-时间图
根据文献[21]可知,车辆在行驶过程中多余的废气排放主要是由车辆在行驶中频繁的加减速造成的,一般情况下,交通状况平顺的路段中二氧化碳排放低于交通状况恶劣的路段.基于此,从图5(a)、5(b)可知,在时变安全距离跟驰模型下,车辆编号为25和50的车辆的二氧化碳排放相较于Konishi跟驰模型降低了50%.对比图5(b)和5(d)可知,的控制器作用下,编号为25和50的车辆的二氧化碳排放得到了进一步的降低,说明该控制器可有效提高车队运行的稳定性,通过图6可进一步验证该结论.综上分析可知,式(21)所示的控制器对于降低废气排放也是有效的.
6 结论
文中提出了一类时变安全距离的CM跟驰模型,并对该模型的稳定性问题进行研究;为了抑制交通拥挤现象,文中设计了一类时滞控制器,并给出了该控制器的设计方法;最后在仿真算例中,对比了Konishi模型和新跟驰模型在抑制交通拥堵和车辆行驶过程中的二氧化碳排放情况,得到以下主要结论:
(1)新的时变安全距离跟驰模型与Konishi模型相比所表现的收敛性更好;
(2)所设计的新CM跟驰模型在滞后控制器下与文献[8]所设计的控制器相比,有效地降低了车队整体的整体震荡幅度和时间;
(3)所设计的控制方法能有效降低车队行驶中的二氧化碳排放量.
本研究对变安全距离的跟驰问题进行了详细的研究,但是仍然有一些问题值得进一步探讨,比如本研究仅对同质车辆下的变安全距离的跟驰问题进行了研究,并未把变安全距离引入到异质车辆环境下,后续工作将对异质车辆的变安全距离进行探讨,以更真实地反映现实交通环境.
[1] YU S,ZHAO X,XU Z,et al.An improved car-following model considering the immediately ahead car’s velocity difference [J].Physica A Statistical Mechanics & Its Applications,2016,461:446- 455.
[2] HEEROO K N S,GUKHOOL O,HOORPAH D.A Ludo cellular automata model for microscopic traffic flow [J].Journal of Computational Science,2016,16:114- 127.
[3] SHARMA S.Lattice hydrodynamic modeling of two-lane traffic flow with timid and aggressive driving behavior [J].Physica A Statistical Mechanics & Its Applications,2015,421(1):401- 411.
[4] YUKAWA S,KIKUCHI M.Coupled-map modeling of one-dimensional traffic flow [J].Journal of the Physical Society of Japan,1994,64(1):35- 38.
[5] YUKAWA S,KIKUCHI M.Density fluctuations in traffic flow [J].Journal of the Physical Society of Japan,1996,65(4):916- 919.
[6] KONISHI K,KOKAME H,HIRATA K.Coupled map car-following model and its delayed-feedback control [J].Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics,1999,60(4):4000- 4007.
[7] ZHAI C,Liu W M,HUANG L,et al.Stability analysis of coupled map car-following model with varying time-delays of drivers [C]∥12th World Congress on Intelligent Control and Automation.[S.l.]:IEEE,2016:303- 307.
[8] ZHAI C,LIU W M. Stability analysis of a class of Takagi-Sugeno fuzzy coupled map car following model with time-delays and control saturation [C]∥International Confe-rence on Advanced Robotics and Mechatronics. Macau:[S.l.],2016:608- 613.
[9] 翟聪,刘伟铭,谭飞刚. 一类耦合映射模糊时滞跟驰系统的反馈控制 [J]. 华南理工大学学报(自然科学版),2017,45(1),9- 17.
ZHAI Cong,LIU Wei-ming,TAN Fei-gang. Feedback control of a class of Coupled-Map fuzzy time-delay car-following system [J]. Journal of South China University of Technology(Natural Science Edition),2017,45(1),9- 17.
[10] HUANG J,YAO J,SUN J,et al.A new coupled map car-following model under inter-vehicle communication [C]∥ International Conference on Control Automation Robotics & Vision.Guangzhou:IEEE,2012,13(1):430- 435.
[11] 葛红霞,程荣军,李志鹏.考虑双速度差效应的耦合映射跟驰模型 [J].物理学报,2011,60(8):94- 103.
GE Hong-Xia,CHENG Rong-Jun,LI Zhi-Peng.Consi-dering two-velocity difference effect for coupled map car-following model [J].Acta Physica Sinica,2011,60(8):94- 103.
[12] 韩祥临,姜长元,葛红霞,等.基于智能交通系统的耦合映射跟驰模型和交通拥堵控制 [J].物理学报,2007,56(8):4383- 4392.
HAN xiang-lin,JIANG Zhang-yuan,GE Hong-xia,et al.A modified coupled map car-following model based on application of intelligent transportation system and control of traffic congestion [J].Acta Physica Sinica,2007,56(8):4383- 4392.
[13] HAN X,CHENG O,LI X.A modified coupled map car-following model considering a nonconstant driver sensitivity [J].Procedia Engineering,2012,31:1045- 1049.
[14] FANG Y,SHI Z.Chaos analysis and delayed-feedback control in a discrete dynamic coupled map traffic model [J].Physica A Statistical Mechanics & Its Applications,2015,422:40- 46.
[15] MCCARTNEY M.A discrete time car following model and the bi-parameter logistic map [J].Communications in Nonlinear Science & Numerical Simulation,2009,14(1):233- 243.
[16] HAN X,Li H,Li X,et al.A modified coupled map car-following model considering of the effect of non-motor vehicles and control of traffic congestion [C]∥International Joint Conference on Computational Sciences & Optimization.[S.l.]:IEEE,2011:1059- 1063.
[17] 孙棣华,周桐,刘卫宁,等.考虑最邻近前车综合信息的反馈控制跟驰模型 [J].物理学报,2013,62(17):170503- 170503.
SUN Di-hua,ZHOU Tong,LIU Wei-ning,et al.A modified feedback controlled car-following model considering the comprehensive information of the nearest-neighbor leading car [J].Acta Physica Sinica,2013,62(17):170503- 170503.
[18] ZHAO X,GAO Z.A control method for congested traffic induced by bottlenecks in the coupled map car-following model [J].Physica A Statistical Mechanics & Its Applications,2006,366(1):513- 522.
[19] FANG Y L,SHI Z K,CAO J L.Congestion phenomenon analysis and delayed-feedback control in a modified coupled map traffic flow model containing the velocity difference [J].Communications in Nonlinear Science & Numerical Simulation,2015,23(1/2/3):175- 184.
[20] ZHENG Y,LEI L,ZHENG P,et al.A modified car-following model with variable safety distance and its nume-rical simulation [J].Asian Journal of Control,2016,18(5):1706- 1713.
[21] TANG T Q,YU Q,YANG S C,et al.Impacts of the vehicle's fuel consumption and exhaust emissions on the trip cost allowing late arrival under car-following model [J].Physica A Statistical Mechanics & Its Applications,2015,431(1):52- 62.
[22] TANG T Q,LI J G,YANG S C,et al.Effects of on-ramp on the fuel consumption of the vehicles on the main road under car-following model [J].Physica A Statistical Mechanics & Its Applications,2015,419(44):293- 300.
[23] MORIMOTO H,ODA T,SUZUKI K,et al.Traffic control aiming for CO2reduction utrizing probe information [C]∥Roceedings of the 16th ITS World Congress and Exhibition on Intelligent Transport Systems and Services.Stockholm:Transportation Research Board,2009:1- 10.
FeedbackControlofCarFollowingModelontheBasisofTime-VaryingSafetyDistance
ZHAICong1,2WUWei-tiao1HUANGLing1LIUWei-ming1ZHENGLi-yuan1
(1. School of Civil Engineering and Transportation, South china University of Technology, Guangzhou 510640, Guangdong, China; 2. School of Transportation and Civil Engineering and Architecture, Foshan University, Foshan 528000, Guangdong, China)
In order to reflect the traffic flow's characteristics more realistically, on the basis of CM (Coupled-Map) car following model proposed by Konishi, a new expression of safely distance is established, with the consideration of the safe distance of vehicles at different speeds. Then, a CM car following model on the basis of time-varying safety distance is proposed subsequently, of which the stability is studied. Moreover, on the basis of stability theory, the sufficient conditions that the traffic congestion phenomenon will never occur are presented, and, in order to suppress the traffic congestion, a delay-feedback controller is designed. Finally, a comparison between the proposed model and Konishi model is made in terms of inhibiting traffic congestion and carbon dioxide emission. Simulated results show that the convergence rate of the proposed model is faster than that of Konishi model, and that the designed controller is effective in suppressing the traffic congestion and reducing the carbon dioxide emission via adjusting motorcade speed.
CM car following model; time-varying safety distance; stability; delay-feedback controller; carbon dioxide emission
2016- 07- 16
国家自然科学基金资助项目(61703165,51408237);中国博士后科学基金资助项目(2016M600653);华南理工大学中央高校基本科研业务费专项资金资助项目(D2171990)
*Foundationitems: Supported by the National Natural Science Foundation of China (61703165,51408237)and the China Postdoctoral Science Foundation (2016M600653)
翟聪 (1989-),男,博士生,主要从事智能交通控制研究.E-mail:957083516@qq.com
†通信作者: 巫威眺 (1987-),男,博士后,主要从事智能交通系统研究.E-mail:ctwtwu@scut.edu.cn
1000- 565X(2017)07- 0126- 09
TP 13
10.3969/j.issn.1000-565X.2017.07.018

