UP整环上的u-平坦模

李 庆

(西南民族大学 计算机科学与技术学院, 四川 成都 610041)

UP整环上的u-平坦模

李 庆

(西南民族大学 计算机科学与技术学院, 四川 成都 610041)

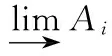
UP整环;u-模;U-内射模;u-平坦模

1 引言及准备知识

在环模理论中,内射性与平坦性的发展一直是众多代数学者研究的焦点问题.2005年,文献[1-2]研究了极大性内射模的概念.2010年,文献[3]刻画了交换环上的极大性内射模并引入了MFG整环等概念并讨论其同调性质.文献[4-6]研究了特殊环上的内射性.2016年,文献[7]在文献[3]的基础上将极大性内射模推广到U-内射模并展开了一系列的讨论.2014年,文献[8]利用w-算子将平坦模推广到w-平坦模.2017年,文献[9]借助于文献[7,10]的思想,定义了u-算子和UP整环,提出了u-正合列的概念,讨论了一些基本的同调性质.希望在文献[9]的基础上进一步较为系统地刻画UP整环上的同调性质,主要对内射性和平坦性做进一步推广研究.

设R是整环,用w-Max(R)表示R的极大w-理想,E(M)表示R-模M的内射包.首先回顾几个重要概念.设S是R的理想的非空集合,满足：

1)R∈S;

2) 若I,J∈S,则IJ∈S,则称S为R的一个理想的乘法系.

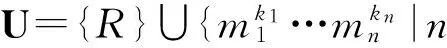
或者对任何J∈U,模同态f:J→M可以扩张到R上,则称M是U-内射模.假设M是U-无挠的R-模,令Mu={x∈K⊗RM|∃J∈U使得Jx⊆M},称Mu为M的u-包络.若J∈U,x∈K⊗RM和Jx⊆M,能推出x∈M,则M就叫做u-模.显然,M是u-模当且仅当Mu=M.由文献[7]中定理3.4可知U-无挠的R-模M是U-内射模,当且仅当M是u-模.在文献[9]中定义了UP整环.所谓R是UP整环,是指R是U-无挠的自U-内射整环且R满足(P).这里R满足(P),是指任意J∈U至少包含一个有限生成子理想I∈U.我们知道u-包络在UP整环上构成了星型算子,简称为u-算子.更多关于u-算子和UP整环的详细介绍参见文献[9].关于星型算子的研究参见文献[11-14].

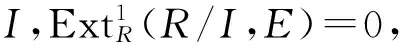
2 UP整环上的内射性研究

本文恒设R是UP整环.

定义2.1[9]设f:M→N是R-模同态.若对R的任何极大u-理想m,有fm:Mm→Nm是单同态(满同态或同构),则称f是u-单同态(u-满同态或u-同构).

定义2.2[9]设A→B→C是R-模同态序列.若对R的任何极大u-理想m,Am→Bm→Cm是正合列,则称此序列A→B→C是u-正合列.

定义2.3设M是任何R-模.若存在有限生成自由模F和u-满同态g:F→M,则称M是u-有限生成R-模.

显然有限生成模是u-有限生成模.由定义可知,若M是u-有限生成R-模,则对任何极大u-理想m,Mm是有限生成的.

命题2.4设M是R-模.

1) 若M是U-挠模,则M是u-有限生成的;

2) 若M是u-有限生成的当且仅当存在M的有限生成子模B,使得对R的任何极大u-理想m,Mm=Bm;

3) 若M是U-无挠模,则若M是u-有限生成的当且仅当存在M的有限生成子模B,使得Mu=Bu,当且仅当Mu是u-有限生成的.

证明1) 由u-正合列0→M→0即得;

2)M是u-有限生成的,则存在有限生成自由模F和u-满同态g:F→M,故gm:Fm→Mm是满同态,故Mm=Im(gm)=Im(g)m,这里令B=Im(g)是M的有限生成子模,因为F是有限生成的,因此Mm=Bm;

3) 由文献[9]中命题3.8和3.9以及上述2)即得.

由文献[7]中例3.10知道U-无挠模的内射模是u-模,反之,则不一定成立.但是可以得出如下结论.

定理2.5设E是u-模,以下各条等价:

1)E是内射模;

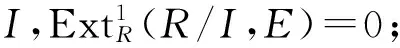
3) 对R的任何u-理想I,同态f:I→E可以扩张到R;

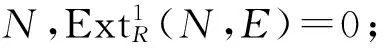
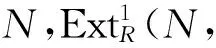
证明1)⟹2)⟹3) 显然成立.

3)⟹1) 设I是R的理想,f:I→E是同态.由文献[9]中定理4.2,f可以扩张为同态g:Iu→Eu=E.由条件g可以扩张到R,故f可以扩张到R.因此,E是内射模.

2)⟹4) 设N=Rx1+…+Rxn,对n做归纳法.当n=1时,即N=Rx1,有正合列0→ann(x1)→R→Rx1→0,故R/ann(x1)≅Rx1=N.因N是U-无挠模,故由文献[9]中命题2.4,ann(x1)是u-理想.故

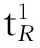
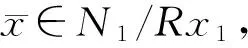
由正合列0→Rx1→N1→N1/Rx1→0,于是

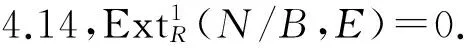
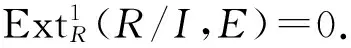
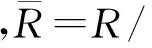
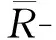
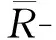
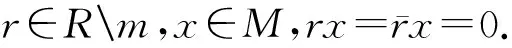
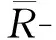
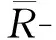
3 UP整环上的u-平坦模

定义3.1设M是R-模,若对任意u-单同态f:A→B,使得1⊗f:M⊗RA→M⊗RB是u-单同态,则称M是u-平坦模.

定理3.2设M是R-模,则:

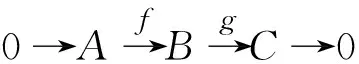
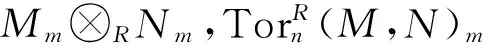
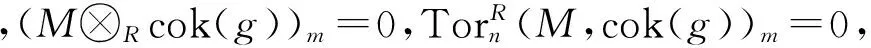
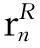
由文献[9]中命题4.4,(Im(f)+ker(g))/Im(f),(Im(f)+ker(g))/ker(g)都是U-挠模.类似于上述证明,由0→Im(f)→Im(f)+ker(g)→(Im(f)+ker(g))/Im(f)→0和0→ker(g)→Im(f)+ker(g)→(Im(f)+ker(g))/ker(g)→0都是正合列,有

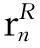
以及

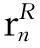
从而

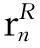
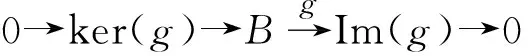
定理3.3设M是R-模,以下各条等价:

1)M是u-平坦模;

2) 对任何u-正合列0→A→B→C→0,序列0→M⊗RA→M⊗RB→M⊗RC→0是u-正合列;

3) 对R的任何极大u-理想m,Mm是平坦Rm-模;

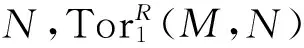
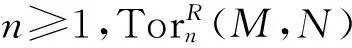
6) 对R的任何理想I,自然同态M⊗RI→IM是u-同构;

7) 对R的任何u-有限生成理想I,自然同态M⊗RI→IM是u-单同态;

8) 对R的任何u-有限生成理想I,自然同态M⊗RI→M是u-单同态.

证明1)⟹2) 由u-平坦模的定义与定理3.2直接得出结论.

2)⟹3) 设Im是Rm任意理想,其中I是R的理想.于是0→I→R→R/I→0是正合列.从而0→M⊗RI→M⊗RR→M⊗RR/I→0是u-正合列.于是,对R的任何极大u-理想m,0→(M⊗RI)m→(M⊗RR)m→(M⊗RR/I)m→0是正合列.故0→Mm⊗RmIm→Mm⊗RmRm→Mm⊗RmRm/Im→0是正合列.故Mm是平坦Rm-模.

4)⟹1) 由定理3.2直接可得结论.

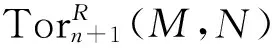
5)⟹4) 显然成立.

3)⟹6)⟹7)⟹8) 易得结论.

8)⟹3) 设m是R的任意极大u-理想,Im是Rm的任意有限生成理想.由假设可知M⊗RI→M是u-单同态.因此,Mm⊗RmIm→Mm是单同态.故Mm是平坦Rm-模.

推论3.41) 若M是U-挠模,则M是u-平坦模.

2) 若f:M→N是u-同构,则M是u-平坦模当且仅当N是u-平坦模.于是,若M是U-无挠模,则M是u-平坦模当且仅当Mu是u-平坦模.

3)M是u-平坦模当且仅当M/torU(M)是u-平坦模,这里torU(M)表示M的U-挠子模.

证明由定理3.3以及文献[9]中命题3.7和3.8直接得出结论.

引理3.5设M是U-无挠模,{Ai|i∈Γ}是M的一簇子模,则:

1) (∑iAi)u=(∑i(Ai)u)u;

2) 若Γ是有限集,则(∩iAi)u=∩i(Ai)u.

证明1) 显然∑iAi⊆∑i(Ai)u,从而

(∑iAi)u⊆(∑i(Ai)u)u.

反过来,设x∈(∑i(Ai)u)u,则存在J∈U使得Jx⊆∑i(Ai)u.因J是有限生成的,故不妨设Jx⊆(A1)u+…+(As)u,于是存在J′∈U使得J′Jx⊆A1+…+As,故x∈(A1+…+As)u⊆(∑iAi)u.

2) 设x∈(∩iAi)u,则存在J∈U使得Jx⊆∩iAi⊆Ai,从而x∈(Ai)u.故x∈∩i(Ai)u.于是(∩iAi)u⊆∩i(Ai)u.反过来,设x∈∩i(Ai)u⊆(Ai)u,因Γ是有限集,于是存在J∈U使得对任意i∈Γ有Jx⊆Ai,从而Jx⊆∩iAi.故x∈(∩iAi)u,于是x∈∩i(Ai)u⊆(∩iAi)u,因此(∩iAi)u=∩i(Ai)u.

定理3.6设0→K→F→M→0是u-正合列,F是u-平坦模,则以下各条等价:

1)M是u-平坦模;

2) 对R的任何理想I,Ku∩(IF)u=(IK)u;

3) 对R的任何有限生成理想I,Ku∩(IF)u=(IK)u.

证明由定理3.3,M是u-平坦模当且仅当对R的任意极大u-理想m,Mm是平坦模.由0→K→F→M→0是u-正合列,于是0→Km→Fm→Mm→0是正合列.从而Mm是平坦模当且仅当对Rm的任何理想(或有限生成理想)Im,其中I是R的任意理想(或有限生成理想),有Km∩ImFm=ImKm,即(K∩IF)m=(IK)m,由文献[9]中命题3.9有(K∩IF)u=(IK)u,再由引理3.5有Ku∩(IF)u=(IK)u.

定理3.70→A→B→C→0是u-正合列,则:

1) 如果A、C是u-平坦模,则B也是u-平坦模;

2) 如果B、C是u-平坦模,则A也是u-平坦模.

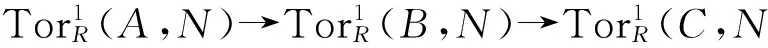
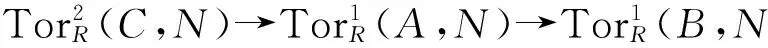
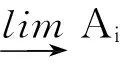
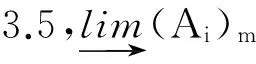
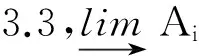
注意,我们知道平坦模是无挠模,但是u-平坦模不一定是无挠模.类似于文献[8]中注3.7,设J∈U,那么R⊕R/J是u-平坦模,但不是无挠模.从而u-平坦模不一定是平坦模.

更正说明:文献[9]中定义2.7中有两处符号印刷错误,将定义2.7这一段的第2行和第3行中K⊕RM修改为K⊗RM.同时文献[9]中命题2.8的证明中第2段的第2行有一处印刷错误,应将K⊕RMi修改为K⊗RMi.为此给读者带来的困扰,作者深表歉意.

致谢西南民族大学中央高校基本科研业务费专项资金(2015NZYQN69)对本文给予了资助,谨致谢意.

[1] WANG M Y, ZHAO G. On maximal injective[J]. Acta Math Sin,2005,21(1):1451-1458.

[2] 赵国,汪明义. 关于极大内射性的注记[J]. 四川大学学报(自然科学版),2005,42(5):859-866.

[3] 王芳贵,汪明义,杨立英. 交换环上的极大性内射模[J]. 四川师范大学学报(自然科学版),2010,33(3): 277-285.

[4] 王芳贵,张俊.w-Noether环上的内射模[J]. 数学学报,2010,53(6):1119-1130.

[5] ZHANG J, WANG F G, KIM H. Injective modules overw-Noetherian rings, II[J]. J Korean Math Soc,2013,50(5):1051-1066.

[6] KIM H, WANG F G. Localization of injective modules overw-Noetherian rings[J]. Bull Korean Math Soc,2013,50(2):475-483.

[7] 李庆,杨军,李高平,等. 交换环上的U-内射模[J]. 四川师范大学学报(自然科学版),2016,39(2):168-173.

[8] KIM H, WANG F G. On LCM-stable modules[J]. J Algebra amp; Its Applications,2014,13(4):1350133.

[9] 李庆. 整环上的u-算子及其同调特征[J]. 四川师范大学学报(自然科学版),2017,40(3):301-307.

[10] 王芳贵. MFG整环上的ε-算子和几乎投射模[J]. 四川师范大学学报(自然科学版),2014,37(5):625-634.

[11] YIN H Y, WANG F G, ZHU X S, et al.w-modules over commutative rings[J]. J Korean Math Soc,2011,48(1):207-222.

[12] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006.

[13] WANG F G, MCCASLAND R L. On strong Mori domains[J]. J Pure Appl Algebra,1999,135(2):155-165.

[14] WANG F G.w-modules over a PVMD[C]//Proc ISTAEM. Hong Kong:Hong Kong Polytechnic University,2001:117-120.

[15] DOBBS D E. On the criteria of D. D. Anderson for invertible and flat ideals[J]. Canad Math Bull,1986,29(1):25-32.

2000MSC：13G05; 13C11; 13D07

(编辑 余 毅)

u-flat Modules over UP-domains

LI Qing

(SchoolofComputerScienceandTechnology,SouthwestUniversityforNationalities,Chengdu610041,Sichuan)

UP domain;u-module;U-injective module;u-flat module

O153.3; O154.2

A

1001-8395(2017)06-0738-05

10.3969/j.issn.1001-8395.2017.06.005

2017-03-14

国家自然科学基金(11401493)和四川省教育厅自然科学基金(14ZB0463)

李 庆(1980—),女,副教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:lqop80@163.com