带逆平方势的非线性Schrödinger方程的阻尼影响

夏 滨

(四川建筑职业技术学院 教务处, 四川 德阳 618000)

带逆平方势的非线性Schrödinger方程的阻尼影响

夏 滨

(四川建筑职业技术学院 教务处, 四川 德阳 618000)

研究一类带逆平方势的阻尼非线性Schrödinger方程,此方程相对论分子物理中有磁性的粒子捕获电子的现象.物理上,阻尼通常弱化系统爆破.从数学上探究分析阻尼对系统爆破的精确影响.对于临界情形,建立一个产生爆破解的阻尼门槛.对于超临界情形,导出一个产生爆破解的阻尼区间.

非线性Schrödinger方程; 逆平方势; 阻尼; 爆破

一类带逆平方势的阻尼非线性Schrödinger方程[1-3]

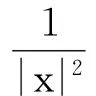
(1)

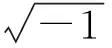
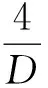
物理上,阻尼通常能够弱化系统爆破.本文旨在从理论上分析探究阻尼对系统爆破的精确影响,发展了M. Tsutsumi[11-12]、G. Fibich[13]、M. Ohta等[14]的方法,对于系统(1)的临界情形,建立一个产生爆破解的阻尼门槛(见定理2.1);对于系统(1)的超临界情形,导出一个产生爆破解的阻尼区间(见定理3.1).

1 预备知识

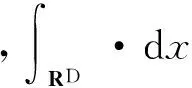
首先赋予方程(1)初值

φ(x,0)=φ0(x),x∈RD.

(2)

于是,(1)和(2)式的局部适定性如下.

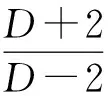
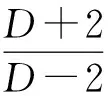
-△u+u-|u|p-1u=0,u∈H1(RD),

(3)

那么Gagliardo-Nirenberg不等式

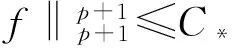
中的最佳常数C*gt;0满足

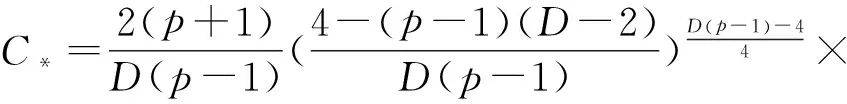
注1.1方程(3)解的存在性见文献[16],唯一性见文献[17].

下面分析Cauchy问题(1)和(2)的特征.

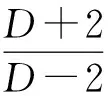
M(φ(t))=e-2atM(φ0)

(4)

和能量方程

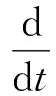
(5)

其中

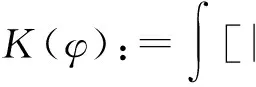
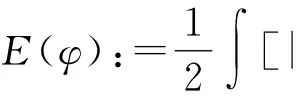
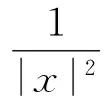
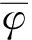
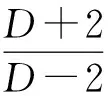
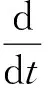
(6)

和

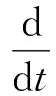
(7)

其中

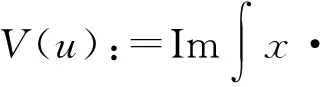
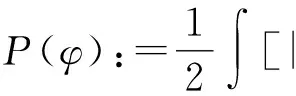
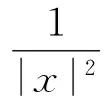
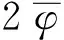
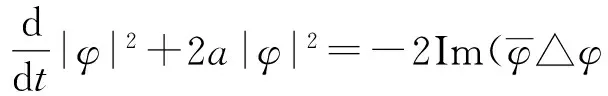
(8)

然后用|x|2乘以(8)式,并在RD上积分可得

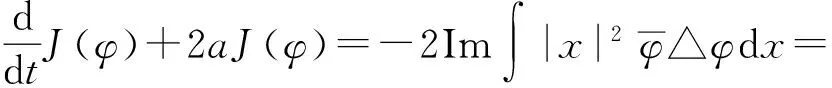
于是可得(6)式.

2)

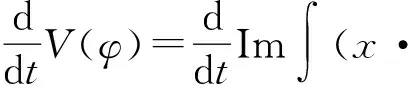
x.

(9)

注意到

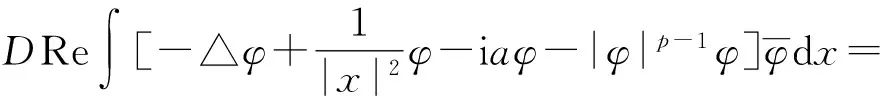
(10)

和

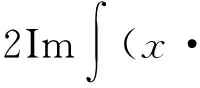
那么由(9)～(11)式易得(7)式成立.命题得证.

下面给出一个变换

v(x,t)=eatφ(x,t),

(12)

其中φ(x,t)是方程(1)的解,那么v(x,t)满足

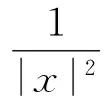
(13)

和

v(x,0)=φ(x,0)=φ0(x).

(14)

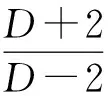
eat‖φ(t)‖2=‖v(t)‖2=‖φ0‖2

(15)

和

H(t):=‖‖
e-a(p-1)t‖
[e-a(p-1)τ‖).

(16)

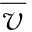
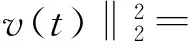
(17)

因此,由(17)和(12)式可得

eat‖φ(t)‖2=‖v(t)‖2=‖φ0‖2.

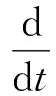
(18)

对(18)式关于t在[0,t]上积分得(16)式.命题得证.

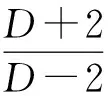
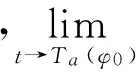
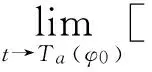
由(15)式可得

‖‖
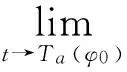
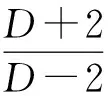
[e-a(p-1)t‖
a(p-1)[e-a(p-1)τ‖

(19)

其中C*是引理1.1中Gagliardo-Nirenberg不等式的最佳常数.

证明由(16)式,引理1.1和(15)式可得

H(0)=H(t)=‖‖
e-a(p-1)t‖
[e-a(p-1)τ‖
‖‖
a(p-1)[e-a(p-1)τ‖
‖‖
‖
‖‖
‖‖
‖
‖‖
‖‖
{e-a(p-1)t‖
[e-a(p-1)τ‖

于是(19)式成立.命题得证.

2 临界情形下的爆破

由物理可知,阻尼能够弱化爆破解[13],阻尼越强,解越容易整体存在,因此,假设(A):对任意给定的初值φ0,系统解的最大存在时间Ta(φ0)关于阻尼参数a单增.

下面给出本文的第一个主要结论.

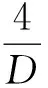
1) 当alt;a*,Cauchy问题(1)和(2)的解φ(t)在有限时间内爆破;

2) 当agt;a*,Cauchy问题(1)和(2)的解φ(t)在H1(RD)中整体存在.

在证明定理之前,先给一些准备结论.

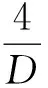
‖φ0‖2≥eaTa(φ0)‖R‖2,

(20)

其中R是方程(3)的正径对称解.

证明用反证法证明.如果(20)式不成立有

‖φ0‖2lt;eaTa(φ0)‖R‖2.

(21)

记g(t):=‖v(t)‖2.由于Cauchy问题(1)和(2)的解φ(t)在有限时间Ta(φ0)爆破,由命题1.5知Cauchy问题(13)和(14)的解v(t)也在Ta(φ0)爆破.进一步有

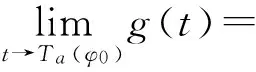
(22)

因此可以声称：存在单增时间序列{tn}使得tn→Ta(φ0)且

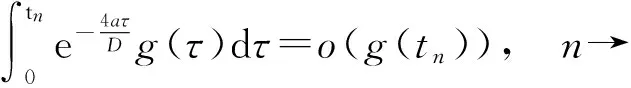
(23)

下面证明(23)式成立.

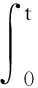
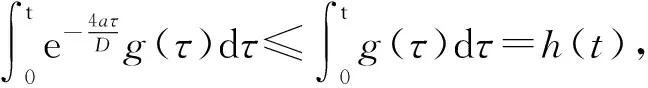
(24)

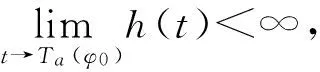
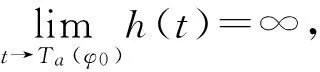
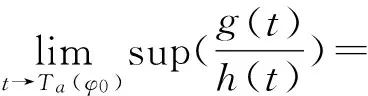
从而一定存在tn→Ta(φ0)使得(23)式成立.

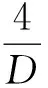
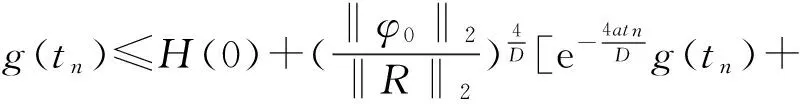
当n→∞得

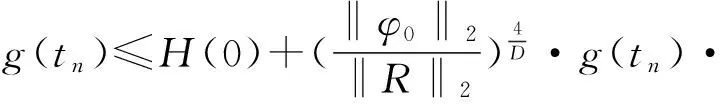
(25)

由(21)和(25)式知g(tn)是有界的,这与(22)式矛盾.命题得证.

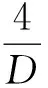
注意到命题2.1仅仅是爆破的一个必要条件,不是充分条件,因为爆破时间Ta(φ0)随阻尼参数a变化而变化.为了获得爆破解的阻尼门槛条件,将运用前面的假设(A).

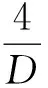
‖φ0‖2≥eaT0(φ0)‖R‖2,

(26)

其中R是方程(3)的正径对称解.

命题2.2直接由假设(A)和命题2.1可推得.

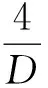
证明由

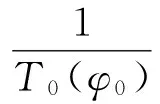
知

‖φ0‖2lt;eaT0(φ0)‖R‖2.

结合到假设(A),于是由命题2.1可立得推论成立.

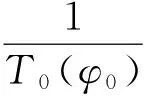
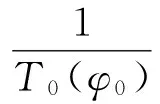
定理得证.

3 超临界情形下的爆破

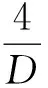
1)E(φ0)lt;0;

2)E(φ0)=0和V(φ0)lt;0;

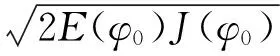
那么一定存在a*(φ0)使得对任意阻尼参数a∈(0,a*(φ0)),Cauchy问题(1)和(2)的解φ(t)在有限时间内爆破.这里泛函E(φ)、V(φ)和J(φ)如命题1.2和1.3中所定义.

证明设初值φ0∈H1(RD)满足|x|φ0∈L2(RD)和定理3.1的条件之一.假设定理3.1的结论不成立,则Cauchy问题(1)和(2)的解φ(t)在t∈[0,+∞)整体存在.

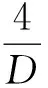
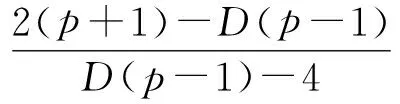
(27)

显然,bgt;0.由命题1.2和1.3知

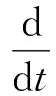
(28)

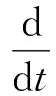
(29)

和

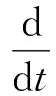
(30)

这里

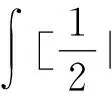
(31)

于是由(30)式可得

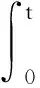
(32)

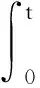
(33)

为了简单起见,记

以及k:=2a+b.

由(27)式有

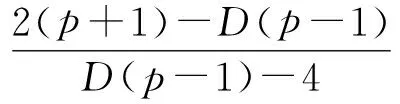
(34)

(33)式变成

(35)

从而

(36)

由(29)式有

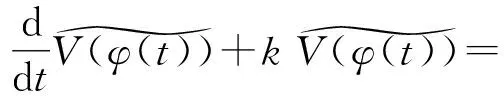
(37)

因此,由(36)和(37)式可知

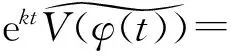
(38)

另一方面,由(28)式和J(φ(t))≥0知

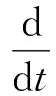
(39)

从而

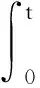
(40)

由(38)和(40)式知

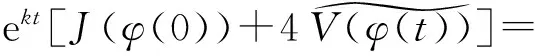
(41)

记

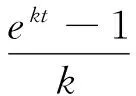
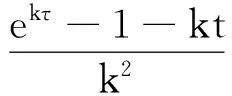
对于f(k,t)关于k运用Taylor展式,对任意的tgt;0有

f(k,t)=f(0,t)+o(k)=
J(φ(0))+4V(φ(0))t+
8E(φ(0))t2+o(k),k→0.

(42)

由于初值φ0满足定理3.1的条件之一,故一定存在Tlt;∞使得

J(φ(0))+4V(φ(0))T+8E(φ(0))T2lt;0,

(43)

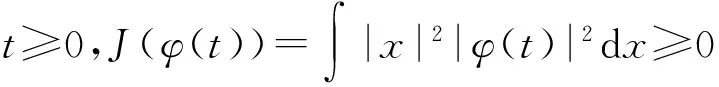
[1] FRANK W M, LAND D J, SPECTOR R M. Singular potentials[J]. Rev Modern Phys,1971,43(1):36-98.

[2] LANDAU L D, LIFSHITZ E M. Quantum Mechanics[M]. London:Pergamon Press Ltd,1965.

[3] LÉVY-LEBLOND J M. Electron capture by polar molecules[J]. Phys Rev,1967,153(1):1-4.

[4] XIA B. Effect of damping for global solution of nonlinear Schrödinger equation with inverse square potential[J]. Mathematica Applicata,2016,29(1):199-207.

[5] BURQ N, PLANCHON F, STALKER J G, et al. Strichartz estimates for the wave and Schroödinger equations with the inverse-square potential[J]. J Functional Analysis,2003,203(2):519-549.

[6] FELLI V, TERRACAINI S. Nonlinear Schrödinger equations with symmetric multi-polar potentials[J]. Cal Var Partial Differential Equations,2006,27(1):25-58.

[7] FELLI V, TERRACAINI S. Elliptic equations with multi-singular inverse-square potentials and critical nonlinearity[J]. Communications in Partial Differential Equations,2006,31(3):469-495.

[8] FELLI V, MARCHINI E M, TERRACINI S. On Schrödinger operators with multipolar inverse-square potentials[J]. J Functional Analysis,2006,250(2):265-316.

[9] FELLI V, MARCHINI E M, TERRACINI S. On Schrödinger operators with multisingular inverse-square anisotropic potentials[J]. Indiana Univ Math Journal,2009,58(2):617-676.

[10] PLANCHON F, STALKER J G, TAHVILDAR-ZADEHD A S.Lpestimates for the wave equation with the inverse-square potential[J]. Discrete Contin Dyn Syst,2003,9(2):427-442.

[11] TSUTSUMI M. Nonexistence of global solutions to the Cauchy problem for the damped nonlinear Schrödinger equations[J]. SIAM J Math Anal,2006,15(2):357-366.

[12] TSUTSUMI M. On global solutions to the initial-boundary value problem for the damped nonlinear Schrödinger equations[J]. J Math Anal Appl,1990,145(2):328-341.

[13] FIBICH G. Self-focusing in the damped nonlinear Schrödinger equation[J]. SIAM J Appl Math,2001,61(5):1680-1705.

[14] OHTA M, TODOROVA G. Remarks on global existence and blowup for damped nonlinear Schrödinger equations[J]. Discrete and Continuous Dynamical Systems,2009,23(4):1313-1325.

[15] BÉGOUT P. Necessary conditions and sufficient conditions for global existence in the nonlinear Schrödinger equation[J]. Adv Math Sci Appl,2002,12(2):817-827.

[16] STRAUSS W A. Existence of solitary waves in higher dimensions[J]. Commun Math Phys,1977,55(2):149-162.

[17] KWONG M K. Uniqueness of positive solutions of △u-u+up=0 inRN[J]. Arch Rat Mech Anal, 1989,105(3):243-266.

MSC2010：78A60; 35Q55

(编辑 郑月蓉)

Effect of Damping for Nonlinear Schrödinger Equation with Inverse Square Potential

XIA Bin

(AcademicAffairsOffice,SichuanCollegeofArchitecturalTechnology,Deyang618000,Sichuan)

This work is to concern the damped nonlinear Schrödinger equation with inverse square potential, which models the process of an electron being captured by polar molecules in non-relativistic molecular physics. We are interested in the effect of the damping in this system. In physics, damping usually weakens the blowup of systems. We analyze and explore the exact effect of the damping in the view of mathematics. For the critical case, a threshold of the damping is established to derive the blowup solution. For the supercritical case, an interval of the damping is constructed to yield the blowup solution.

nonlinear Schrödinger equation; inverse square potential; damping; blowup

O175.29

A

1001-8395(2017)06-0802-07

10.3969/j.issn.1001-8395.2017.06.016

2016-09-10

国家自然科学基金(11571245)和四川省教育厅重点科研项目(15ZA0031)

夏 滨(1969—),男,副教授,主要从事应用非线性分析的研究,E-mail:xiabin690215@163.com