关于FT-投射与自内射环

沈 磊， 王芳贵， 王 茜

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

关于FT-投射与自内射环

沈 磊， 王芳贵*， 王 茜

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

有限投射分解; FT-投射模; fPD(R); 自内射环; 凝聚正则环

自内射环是一类具有重要应用意义的环，学者们用不同的方法来刻画自内射环的性质，参见文献[1-4].文献[5]称R-模M有有限投射分解(finite projective resolution)，简记为M∈FPR(R)，是指若存在正合列

0→Pn→Pn-1→…→P1→P0→M→0,

其中每个Pi是有限生成投射模.若M∈FPR(R)，则M是有限表现模.文献[6]重新定义环R小finitistic维数为

fPD(R)=sup{pdRM|M∈FPR(R)}.

这是对文献[7]定义的小finitistic维数的修正.文献[8]利用有限投射分解的模类引入了FT-内射模和FT-平坦模的概念，研究了相应的同调维数，对环的小finitistic维数给出了一个新的刻画.为了刻画自内射环的同调性质，本文利用有有限投射分解的模类引入了FT-投射模和FT*-内射模的概念，证明了自内射环其实就是FT-投射意义下的半单环.同时还得到了，对自内射环R，有fPD(R)=0.

本文恒设R为有单位元的结合环.如未特别声明，模都是左模，理想都是左理想.凝聚环，自内射环和遗传环等分别指左凝聚环，左自内射环和左遗传环.

1 FT-投射模

例1.11) 若R-模M是有限生成投射模，则M∈FPR(R);

2) 若R是凝聚环，M是有限表现R-模，且pdRMlt;∞，则M∈FPR(R).

显然，投射模，Gorenstein投射模，文献[9-10]中的FP-投射模和文献[11-12]中的P-投射模都是FT-投射模.

命题1.3设P是R-模，则下列各条等价:

1)P是FT-投射模;

2) 对任何满同态g:B→C，若ker(h)∈FPR(R)，则对任何同态f:P→C，存在同态h:P→B，使得f=gh;

3) 若ξ:0→A→B→C→0是正合列，其中A∈FPR(R)，则HomR(P，ξ)也是正合列;

4) 任何形如0→A→B→P→0的正合列分裂，其中A∈FPR(R).

证明1)⟹3)⟹2) 显然;

3)⟹4) 由文献[13]的命题7.24即得;

3)⟹1) 设M∈FPR(R)，E(M)为M的内射包，令C=E(M)/M则有正合列

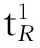
命题1.4FT-投射模对直和，直和加项以及模扩张是封闭的.

设0→A→B→C→0是正合列，A，C是FT-投射模，则有正合列

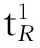
关于FT-投射模也有类似于投射模的Schanuel引理.

命题1.5设0→K1→P1→M→0与0→K2→P2→M→0是正合列，其中P1是FT-投射模，K2∈FPR(R)，则有以下2条成立:

2) 若还有P2是FT-投射模，K1有FPR，则K2⊕P1≅K1⊕P2.

证明1) 由假设，存在同态h:P1→P2，使得f=gh，于是图1右边方图诱导同态σ:K1→K2，使得左边方图也是交换图

图 1

由文献[7]的定理2.5.7得，图1左边的方图是一个推出图，故

0→K1→K2⊕P1→P2→0

是正合列;

2) 由1)和命题1.3即得.

称投射模P为忠实投射模，若P是忠实平坦模.

命题1.6设R，T是环，P是(R，T)-双模，下列各条成立:

1) 若P是FT-投射R-模，则对任何投射左T-模Q，都有P⊗TQ是FT-投射左R-模;

沉箱海测及陆侧抛石棱体范围计划采用1艘8方挖泥船进行开挖，抓斗船平行码头方向布设，与码头预留约2米的安全距离。8方抓斗船吊臂长度大于27米，抓斗更换为4～6方的小斗，放低吊臂从侧面伸入码头后方进行清挖，吊臂与水平面的角度约55°～60°，抓斗可开挖距离大于13米，可满足清挖要求。泥驳靠泊在挖斗船外侧，为了便于抓斗放渣，泥驳靠在抓斗船船尾。一次驻船可同时清挖码头海侧和陆侧区域，海侧和陆侧区域错位距离约12米，为保证沉箱安全，先清挖陆侧区域再清挖海侧区域，且内外标高落差不得大于2米。

2) 若P是FT-投射R-模，则对任何有限生成投射右T-模Q，都有HomT(Q，P)是FT-投射R-模;

3) 若对任何有限生成忠实投射右T-模Q，都有HomT(Q，P)是FT-投射R-模，则P是FT-投射R-模.

2 FT*-内射模

本节再给出FT*-内射模的概念与性质，以便更好的用FT-投射模刻画环的结构.

定义2.1称R-模N为FT*-内射模，是指对任何单同态g:A→B，若A∈FPR(R)，则对任何同态f:A→N，存在同态h:B→N，使得f=hg.

显然，内射模是FT*内射模.

命题2.2设E是左R-模，则下列各条等价:

1)E是FT*-内射模;

2) 对任何正合列ξ:0→A→B→C→0，若A∈FPR(R)，则HomR(ξ，E)也是正合列.

命题2.3设E∈FPR(R)，则E是FT*-内射模当且仅当E是内射模.

证明设E是FT*-内射模，ξ:0→E→B→C→0是正合列.记f:E→B，则对恒等同态1E，存在h:B→E，使得hf=1E，从而ξ分裂，故E是内射模.

推论2.4设A是R-模B的子模，若A∈FPR(R)是FT*-内射模，则A是B的直和加项.

证明设ξ:0→A→B→C→0是正合列，且A∈FPR(R).由交换图

即得.

3 自内射环的同调刻画

接下来用以上提到的2类模来刻画环.

定理3.1以下各条等价:

1) 任何R-模是FT*-内射模;

2) 任何R-模是FT-投射模;

3) 任何有限生成R-模是FT-投射模;

4) 任何循环R-模是FT-投射模;

5) 任何M∈FPR(R)是内射模;

6) 任何有限生成投射R-模是内射模;

7)R是自内射环.

证明1)⟹2) 设M是R-模，0→A→B→M→0是正合列，且A∈FPR(R)，由命题2.3知A是内射模，从而该正合列分裂，由命题1.3得M是FT-投射模;

2)⟹3)⟹4) 显然;

5)⟹1) 设N是R-模，ξ:0→A→B→C→0是正合列，且A∈FPR(R).由假设A是内射模，从而ξ分裂，故HomR(ξ，N)也是正合列，由命题2.2得N是FT*-内射模;

5)⟹6)⟺(7) 显然;

6)⟹5) 设M有如下分解

0→Pn→Pn-1→…→P1→P0→M→0,

其中每个Pi是有限生成投射模，记K0=ker(P0→M)，Ki=ker(Pi→Pi-1)，i=1，2,…，n，并约定K-1=M.由假设Kn-1=Pn是内射模，故正合列

0→Kn-1→Pn-1→Kn-2→0

分裂，从而Kn-2是有限生成投射模.再由正合列

0→Kn-2→Pn-2→Kn-3→0，

可得Kn-3是有限生成投射模.重复此步骤，可得M是有限生成投射模，从而是内射模.

由上述定理的证明过程中可以直接得到：

推论3.2设R是自内射环，M是R-模，则M∈FPR(R)当且仅当M是有限生成投射模.从而fPD(R)=0.

例3.3R=Z4是自内射环，但不是半单环，因此存在一个不是投射模的FT-投射模，如M=2Z4.也存在不是内射模的FT*-内射模.

文献[6]称环R为(同调)正则环，是指R的每个有限生成理想的投射维数有限.环R是von Neumann正则环[14](简记为VN正则环)，当且仅当每个R-模都是平坦模，当且仅当每个主理想由一个幂等元生成，当且仅当任何主理想是R的直和加项.

引理3.4设R是凝聚环，则R是(同调)正则环当且仅当任何有限表现左R-模的投射维数有限.

证明见文献[5]定理6.2.1.

命题3.5设R是自内射环，且任何主理想有有限投射分解，则R是VN正则环.

证明设I是R的主理想，由定理3.1得I是内射模，从而I是R的直和加项.

推论3.6设R是凝聚(同调)正则环，且为自内射环，则R是VN正则环.

证明由引理3.4和命题3.5即得.

命题3.7设R是凝聚(同调)正则环，M是有限表现R-模，则M是FT-投射模当且仅当M是投射模.

证明设M是FT-投射模，取正合列ξ:0→K→F→M→0，其中F是有限生成自由模，则K是有限生成的.又R是凝聚环，从而K是有限表现的.又R是同调正则环，由引理3.4得K的投射维数有限，从而K∈FPR(R)，由命题1.3，正合列ξ分裂，于是有F≅K⊕M，故M是投射模.

文献[5]称交换环R上的模M为可除模，是指对任何非零因子a∈R，以及任何x∈M，存在y∈M，使得x=ay.

命题3.8设交换环R是凝聚(同调)正则环，则FT*-内射模是可除模.

证明设M是FT*-内射模，x∈M，且a∈R是非零因子，I=(a)是有限表现的，再由引理3.4得pdRIlt;∞，从而I∈FPR(R).于是同态f:I→R，f(ra)=rx，可以扩张为同态g:R→E.令y=g(1)，得ay=g(a)=f(a)=x，故E是可除模.

4 FT*-遗传环

定义4.1称R为FT*-遗传环，如果任何FT-投射模的子模仍是FT-投射模.

显然遗传环和自内射环是FT*-遗传环.再由命题1.3可得:

命题4.2设R是FT*-遗传环，0→A→B→C→0是正合列，且C是FT-投射模，则A是FT-投射模当且仅当B是FT-投射模.

定理4.3下列各条等价:

1)R是FT*-遗传环;

2) 投射R-模的子模是FT-投射模;

3) 由R-模的子模是FT-投射模;

4) 任何理想是FT-投射模;

5) 若M∈FPR(R)，则idRM≤1.

证明1)⟹2)⟹3)⟹4) 显然;

[1] GOODEARL K R, HANDELMAN D. Simple self-injective rings[J]. Commun Algebra,1975,3(9):797-834.

[2] BO S. Rings of Quotients[M]. Berlin Heidelberg:Springer-Verlag,1975.

[3] FAITH C. Self-injective rings[J]. P Am Math Soc,1979,77(2):157-164.

[4] UTUMI Y. Self-injective rings[J]. J Algebra,1967,6(1):56-64.

[5] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006.

[6] GLAZ S. Commutative Coherent Rings[M]. Berlin Heidelberg:Springer-Verlag,1989.

[7] BASS H. Finitistic dimension and a homological generalization of semi-primary rings[J]. T Am Math Society,1960,95(3):466-486.

[8] 孙小武. FT-内射模与FT-平坦模[D]. 成都:四川师范大学,2015.

[9] 黄影. 关于FP-投射模[J]. 吉林师范大学学报(自然科学版),2007,28(1):47-48.

[10] 吴雅丽. FP-投射模与强GFP-内射模[D]. 成都:四川师范大学,2015.

[11] 苗佳晶. 关于P-投射模[J]. 吉林师范大学学报(自然科学版),2007,28(3):109-110.

[12] 徐龙玉,王芳贵,陈翰林. P-投射模的刻画[J]. 四川师范大学学报(自然科学版),2013,36(4):500-503.

[13] ROTMAN J J. An Introduction to Homological Algebra[M]. New York:Academic Press,1979.

[14] GOODEARL K R. Von Neumann Regular Rings[M]. London:Pitman,1979.

[15] ANDERSON F W. Rings and Categories of Modules[M]. New York:Springer-Verlag,1974.

[16] MAO L X, DING N Q. FP-projective dimension[J]. Commun Algebra,2005,33(4):1153-1170.

[17] ENOCHS E E. A note on absolutely pure modules[J]. Can Math Bull,1976,19(19):361-362.

MSC2010:16D50; 16E50

(编辑 陶志宁)

On FT-Projective Modules and Self-Injective Ring

SHEN Lei, WANG Fanggui, WANG Xi

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

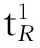
FT-projective modules; finite projective resolution; fPD(R); self-Injective rings; coherent regular rings

O153

A

1001-8395(2017)06-0727-04

10.3969/j.issn.1001-8395.2017.06.003

2016-08-31

国家自然科学基金(11671283)

*通信作者简介:王芳贵(1955—)，男，教授，主要从事交换代数、同调代数与代数K理论的研究,E-mail:wangfg2004@163.com