非自治反映扩散方程后项紧拉回吸引子的存在性

佘连兵, 王仁海

(1. 六盘水师范学院 数学与信息工程学院, 贵州 六盘水 553004; 2. 西南大学 数学与统计学院, 重庆 400715)

非自治反映扩散方程后项紧拉回吸引子的存在性

佘连兵1, 王仁海2

(1. 六盘水师范学院 数学与信息工程学院, 贵州 六盘水 553004; 2. 西南大学 数学与统计学院, 重庆 400715)

给出了定义在Banach空间上的非自治过程存在唯一的后项紧的拉回吸引子的一个充分条件，运用此理论证明了非自治反映扩散方程在相对弱的假设条件下存在唯一的后项紧拉回吸引子.

非自治动力系统; 拉回吸引子; 后项紧性; 非自治反映扩散方程

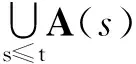
ut+λu-Δu=f(x,u)+g(t,x),x∈E,

(1)

其中,E是RN中的有界域,t≥s∈R,λgt;0且u(s,s,x)=u0.

关于非自治动力系统的详细介绍可见文献[3,5].此外，为了方便后面的后项一致估计，把文献[4]中的Gronwall型不等式写成下面的具有非自治形式的后项Gronwall型不等式(这里对过去的时间取上确界).设y、y′、y1和y2是R上的局部可积函数,且y、y1和y2是非负的，对于每个t∈R满足

y′(s)+by(s)+y1(s)≤y2(s),s≤t.

(i) 若b∈R是一个给定的常数，则对于每一个t∈R和μgt;0有

(2)

(ii) 若b≥0是一个给定的常数，则对于每一个t∈R和μgt;0有

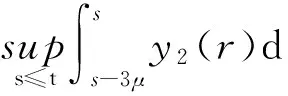
(3)

1 后项紧拉回吸引子理论

定义1.1设S(t,s):X→X,∀t≥s是定义在Banach空间X上的一族映射,若对于任意的t≥r≥s有S(s,s)=idx，S(t,s)=S(t,r)S(r,s)，则称S是X上的一个非自治过程.

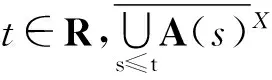
定义1.3设A={A(t)}t∈R是Banach空间X中的一个非自治集,对任意的t1,t2∈R,当t1≤t2时，有A(t1)⊂A(t2),则称A是单调递增的；当t1≤t2时，有A(t1)⊃A(t2),则称A是单调递减的.

定义1.4设S是定义在Banach空间X上的一个非自治过程,若X中的一个非自治集A={A(t)}t∈R满足：

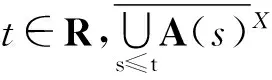
2)A是不变的，即S(t,τ)A(τ)=A(t),t≥τ;

3)A是拉回吸引的，即对于X中每个有界集D有

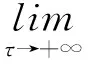
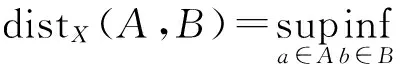
定理1.1设S是定义在Banach空间X上的一个非自治过程，若

(i) S在X上有一个单调递增的有界闭吸收集K={K(t)}t∈R,

(ii)S是后项ω极限紧的,即

则S有一个后项紧的拉回吸引子A={A(t)}t∈R,其中κX(·)是文献[3]中介绍的Kuratowski测度，

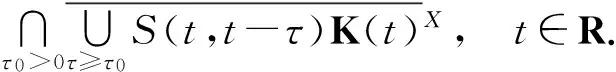
(4)

证明设B(X)是X中有界集的全体.条件(i)和(ii)满足文献[8]中的定理2.23,因此S有一个拉回吸引子A={A(t)}t∈R,其中A(t)由(4)式给出.

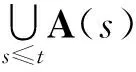
A(s)=ωX(K(s),s)=

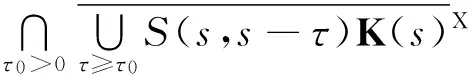
k(s)⊂k(t)⊂D,

(5)

让τn→+∞当n→+∞，由A的不变性和(5)式知

A(sn)=S(sn,sn-τn)A(sn-τn)⊂

S(sn,sn-τn)D,

(6)

由(6)式和yn∈A(sn)知，存在xn∈D,使得

yn=S(sn,sn-τn)xn, xn∈D.

(7)

因为τn→+∞当n→+∞,所以存在Ngt;0使得当n≥N时有τn≥τ1.又由(ii)知∀εgt;0,D∈B(X)存在τ0gt;0使得

ε.

(8)

从而由(7)和(8)知

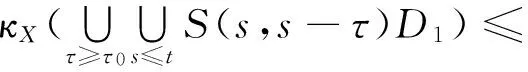
(9)

此外,容易证明以下性质：

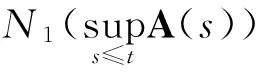
性质2如果S在X上存在一个后项紧的拉回吸引子A,则A一定唯一的且是X中所有闭的拉回吸引集中最小的；

性质3S在X中有一个单调递增的有界的吸收集等价于S在X中有一个后项有界的吸收集.

2 后项紧拉回吸引子的存在唯一性

本章将证明方程(1)在相对弱的假设条件下存在唯一的后项紧拉回吸引子,为了方便计算，设c是变化的正常数.

假设F设pgt;2,β1,β2,β3gt;0,f(·,·)∈C1(E×R,R)满足

f(x,u)u≤-β1|s|p+ψ1, ψ1∈L2(E), (10)

|f(x,u)|≤β2|s|p-1+ψ2,ψ2∈L2(E),(11)

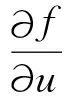
由于研究的是有界域,故ψi(i=1,2,3)也可以换成一般的常数.

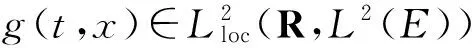
‖g(r,·)‖2drlt;∞, ∀t∈R.(12)

此假设条件比文献[5]中的假设条件弱,但仍然能得到想要的结果,这是因为文献[5]做了如下假设：外力项是后项平移有界的,即

‖g(r,·)‖2drlt;∞,

∃t∈R,agt;0,

(13)

且作者证明了(13)式与

‖g(r,·)‖2drlt;∞,

∀t∈R,λgt;0

(14)

是等价的.因此容易得出假设G比假设(13)弱.

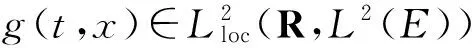
u(·,s,u0)∈C([s,+∞),L2(E))∩

(15)

特别地,u(s,s,u0)=u0,于是由适定性可以定义如下非自治过程S(·,·):L2(E)→L2(E):

S(t,t-τ)u0=u(t,t-τ,u0),
∀u0∈L2(E),τ≥0.

(16)

定理2.1若假设F和G成立,则∀t∈R,u0∈D∈B(L2(E)),存在一个τ0=τ0(D)gt;3,使得对∀τ≥τ0有

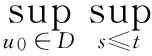
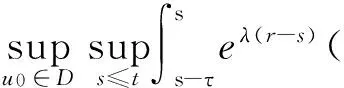
其中

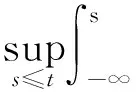
此外，S在L2(E)上有一个单调递增的有界吸收集.

证明让(1)式与u做内积可得

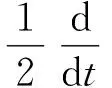
(20)

由Young不等式及(10)式可知(20)式右边满足

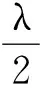
(21)

由(20)和(21)式知

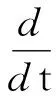
(22)

在[s-τ,s]上对(22)式用经典的Gronwall不等式,并由u(s-τ,s-τ,u0)=u0得

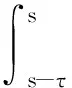
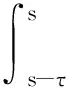
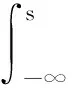
由u0∈D∈B(L2(E))，于是存在一个τ0=τ0(D)gt;3使得当τ≥τ0时有

‖u(s,s-τ,u0)‖2+

(24)

于是(17)和(18)式成立.记

H(t)={w∈L2(E):‖w‖2≤c(1+M(t))},

t∈R.

(25)

由假设G知M(t)是有界且单调递增的,故由(17)式知H={H(t)}t∈R是L2(E)上的一个单调递增的有界闭吸收集.

引理2.1若假设F和G成立,对∀t∈R,u0∈D∈B(L2(E)),则存在一个τ0≥3,使得对∀τ≥τ0有

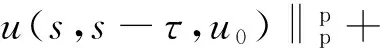
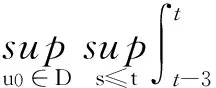
ceλt(1+M(t)).

(26)

证明将(1)式与|u|p-2u做内积,可得

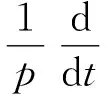
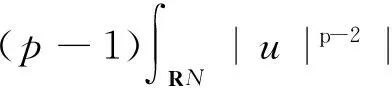
(27)

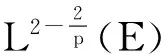
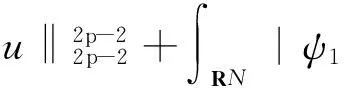
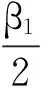
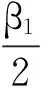
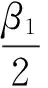
(28)

由Young不等式知

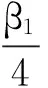
(29)

于是由(27)～(29)式知

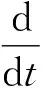
c‖g(t,·)‖2+c.

(30)

当μ=1,b=0时，对(30)式运用后项Gronwall型不等式,并由(18)和(19)式知当τ≥τ0gt;3时有

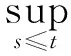
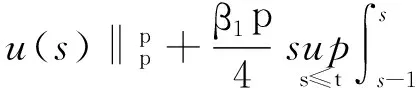
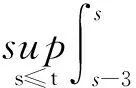
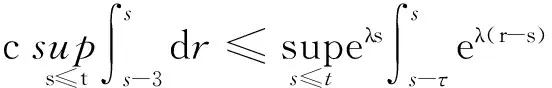
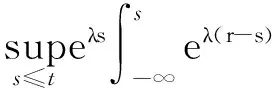
ceλt(1+M(t)),

(31)

于是(26)式成立.

下面估计解在H1(E)上的吸收性.

引理2.2若假设F和G成立,则对∀t∈R,u0∈D∈B(L2(E)),存在一个τ0≥3,使得对∀τ≥τ0有

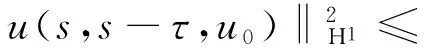
ceλt(1+M(t)).

(32)

证明让(1)式与ut做内积可得

(33)

由Young不等式及(10)式可得

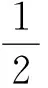
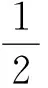
(35)

由(33)～(35)式得

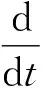
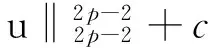
(36)

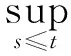
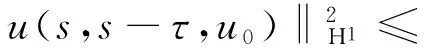
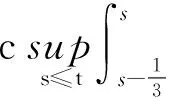
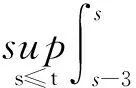
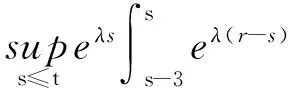
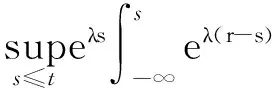
ceλt(1+M(t)),

(37)

于是(32)式成立.

定理2.2若假设F和G成立,则(16)式中的非自治过程S是后项ω极限紧的.

证明定义一个时间依赖的集合

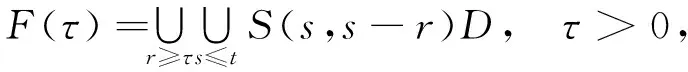
其中D是L2(E)上的任意有界集，容易看出F(τ)关于τ是单调递减的，由引理2.2知,存在τ0gt;3，当τ≥τ0时有F(τ)是H1(E)中的有界集,由Sobolev紧嵌入定理知F(τ)是L2(E)中的预紧集,故由文献[3]中的引理2.7(c)可知∀εgt;0,κL2(E)F(τ)lt;ε,因此

(38)

所以(16)式中的非自治过程S是后项ω极限紧的.

定理2.3在L2(E)中,非自治的反映扩散方程(1)在假设F和G下有一个单调递增的有界闭吸收集H={H(t)}t∈R,其中H(t)由(25)式给出,且有唯一的后项紧拉回吸引子A={A(t)}t∈R,其中

A(t)=ωX(H(t),t)=

(39)

证明由定理2.1和定理2.2可知定理1.1的条件(i)、(ii)满足,故由定理1.1知定理2.3成立.

[1]CARABALLOT,CARVALHOAN,LANGAJA,etal.Existenceofpullbackattracttorsforpullbackasymptoticallycompactprocesses[J].NonlinearAnal,2010,72(3):1967-1976.

[2]WANGBX.Sufficientandnecessarycriteriaforexistenceofpullbackattractorsfornon-compactrandomdynamicalsystems[J].JDiffEqns,2012,253(5):1544-1583.

[3]LIYR,GUAH,LIJ.Existenceandcontinuityofbi-spatialrandomattractorsandapplicationtostochasticsemilinearLaplacianequations[J].JDiffEqns,2015,258(2):504-534.

[4]LIYR,YINJY.AmodifiedproofofpullbackattractorsinaSobolevspaceforstochasticFitzHugh-Nagumoequations[J].DisreteContinDynSyst,2016,21(4):1203-1223.

[5]CUIHY,LANGAJA,LIYR.Regularityandstructureofpullbackattractorsforreaction-diffusiontypesystemswithoutuniqueness[J].NonlinearAnal,2016,140:208-235.

[6]LIYR,WANGRH,YINJY.Bankwardcompactattratorsfornon-autonomousBenjsmin-Bona-Mahonyequationsonunboundedchannels[J].DiscreteContinDynSyst,2017,B22(7):2569-2586.

[8]CARVALHOAN,LANGAJA,ROBINSONJC.AttractorsforInfinite-dimensionalNon-autonomousDynamicalSystems[M].NewYork:Springer-Verlag,2013:182.

2010MSC:35K57; 35B41

(编辑 周 俊)

The Backward Compactness of Pullback Attractors for Nonautonomous Reaction-Diffusion Equations

SHE Lianbing1, WANG Renhai2

(1.DepartmentofMathematics,LiupanshuiNormalCollege,Liupanshui553004,Guizhou;2.SchoolofMathematicsandStatistics,SouthwestUniversity,Chongqing400715)

A sufficient condition for the existence of a unique and backward compact pullback attractor for a nonautonomous process defined on the Banach space is established. This result is applied to prove that the nonautonomous reaction-diffusion equation has a unique and backward compact pullback attractor under some relative weak assumptions.

nonautonomous dynamic systems; pullback attractor; backward compactness; nonautonomous reaction-diffusion equation

O117.8

A

1001-8395(2017)06-0797-05

10.3969/j.issn.1001-8395.2017.06.015

2016-11-15

国家自然科学基金(11571283)、贵州省教育厅自然科学基金(KY[2016]103和KY[2016]271)和贵州省科学技术基金(LP[2015]7612和LKLS[2013]14)

佘连兵(1981—),男,副教授,主要从事微分方程和无穷维动力系统的研究,E-mail:shelianbing@163.com