一类四阶微分方程m点边值问题的正解

赵 微

(大庆师范学院 教师教育学院, 黑龙江 大庆 163712)

一类四阶微分方程m点边值问题的正解

赵 微

(大庆师范学院 教师教育学院, 黑龙江 大庆 163712)

讨论一类四阶微分方程m点边值问题

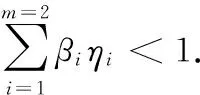
四阶微分方程;m点边值问题; 正解; 锥; 不动点指数

四阶微分方程的边值问题在弹性力学和工程物理中，常用来刻画弹性梁的平衡状态.由于这类问题应用很普遍，因此，许多学者对这类问题进行了深入的研究，并得到许多结果.对于四阶常微分方程两点或三点边值问题正解的存在性，一些学者已经做了较多的研究[1-6].然而对于四阶常微分方程m点边值问题的研究相对较少，并且大多运用Krasnoselskii’s不动点定理或上下解方法[7-8].

文献[4]主要研究一类四阶三点边值问题

运用不动点指数定理得到了上述问题正解的存在性.

受文献[4]的启发，本文将上述三点边值推广到m点边值，即考虑如下奇异四阶微分方程边值问题

(1)

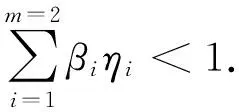
1 准备工作

为了方便,作如下假设条件:

(H2)h:(0,1)→[0,∞)连续,h(t)不恒等于0.允许h(t)在t=0,1处奇异,且

(2)

(H3)f:[0,+∞)→[0,+∞)连续.

定义1如果u(t)满足如下条件:

(ⅰ)u(t)∈C[0,1],且于(0,1)内大于0;

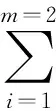
则u(t)是(1)式的正解.

引理1函数g(t,s)满足

g(t,s)≤s(1-s), 0≤t,s≤1,

(3)

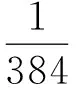
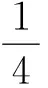
(4)

证明令

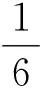
0≤s≤t≤1,

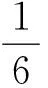
0≤t≤s≤1,

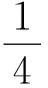
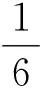
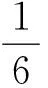
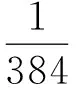
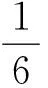
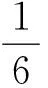
当0≤t≤1时有

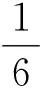
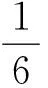
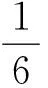
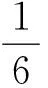
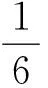
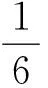
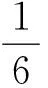
证毕.

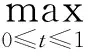
P={u∈C[0,1]:u(t)≥0,t∈[0,1]},

则P是C[0,1]上的正锥,取

‖u‖},

定义算子

t∈[0,1].

(5)

引理2设条件(H1)～(H3)满足,则算子A:P1→P1全连续.

证明由(3)式可知

于是

则有

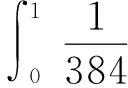
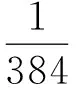
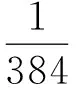
从而A:P1→P1,且A(P1)→P1.

由Azela-Ascoli定理则知,算子A:P1→P1全连续.证毕.

定义算子

t∈[0,1],

(6)

易知T是线性全连续算子.

引理3设条件(H1)～(H3)满足,则由(6)式定义的算子T的谱半径r(T)≠0,且T有关于第一特征值λ1=(r(T))-1的特征函数.

证明类似于文献[9]中的引理3.

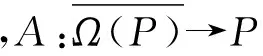
u-Au≠μu0, ∀u∈∂Ω(P),μ≥0,

则不动点指数

i(A,Ω(P),P)=0.

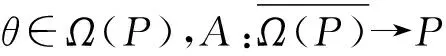
Au≠μu, ∀u∈∂Ω(P),μ≥1,

则不动点指数

i(A,Ω(P),P)=1.

2 主要结论

定理1如果假设(H1)～(H3)满足,且

(7)

(8)

其中λ1是由(6)式定义的算子T的第一特征值，则四阶边值问题(1)至少存在一个正解.

证明由(7)式知,存在r1gt;0,使得∀0≤u≤r1,有f(u)≥λ1u.设u*是T的关于λ1的特征函数,则u*=λ1Tu*.

因为f(u)≥λ1u,∀0≤u≤r1,所以有

假设A在∂Br1∩P1上没有不动点(否则结论成立).现证u-Au≠μu*,μ≥0,否则,存在μ1及τ0≥0,使得u1-Au1=τ0u*,显然可知τ0gt;0,且

u1=Au1+τ0u*≥τ0u*.

令τ*=sup{τ|u1≥τu*},则显然有τ*≥τ0gt;0,且u1≥τ*u*.又因为T(P1)⊂P1,则有

λ1T(u1)≥λ1T(τ*u*)=

τ*λ1Tu*=τ*u*,

因此

u1=Au1+τ0u*≥λ1T(u1)+τ0u*≥

τ*u*+τ0u*=(τ*+τ0)u*,

此与τ*的定义相矛盾,故假设不成立，所以,有u-Au≠μu*,μ≥0，因此,由引理4有

i(A,Br1∩P1,P1)=0.

(9)

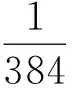
(T1u)(t)=σλ1(Tu)(t),

∀u∈C[0,1],

则显然有T1:C[0,1]→C[0,1]是有界线性全连续算子,且T1(P1)⊂(P1).

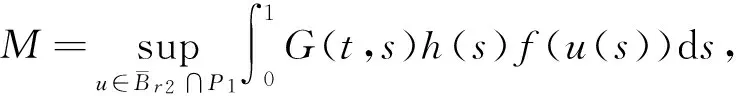
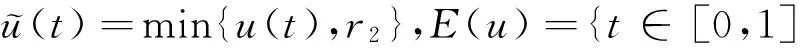
u(t)=μ(Au)(t)=

于是(I-T1)(u)≤M.

由于λ1是T的第一特征值,且0lt;σlt;1,所以有(r(T1))-1gt;1,因此(I-T1)-1存在,且

从T1(P1)⊂P1,及上式得知(I-T1)-1(P1)⊂P1,于是有u(t)≤(I-T1)-1M,故W是有界的.

取r3gt;max{r2,supW}.由不动点的同伦不变性知

i(A,Br3∩P1,P1)=

i(θ,Br3∩P1,P1)=1.

(10)

由(9)和(10)式可知

i(A,Br3∩P1,P1)-i(A,Br1∩P1,P1)=

1-0=1，

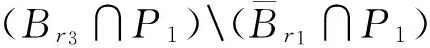
定理2如果假设(H1)～(H3)满足,且

(11)

(12)

其中λ1是由(6)式定义的算子T的第一特征值,则四阶边值问题(1)至少存在一个正解.

证明由(11)式知,存在r1gt;0,使得f(u)≤λ1u,0≤u≤r1.定义(T2u)(t)=λ1(Tu)(t),∀u∈C[0,1],因此,T2:C[0,1]→C[0,1]是线性全连续有界算子,且T2(P1)⊂P1,r(T2)=1,于是,∀u∈∂Br1∩P1,则有

(T2u)(t),

于是(Au)(t)≤(T2u)(t),∀u∈∂Br1∩P1.假设A在∂Br1∩P1上无不动点(否则,结论成立).现证Au≠μu,∀u∈∂Br1∩P1,μ≥1,否则,存在μ0≥1,u1∈∂Br1∩P1,使得Au1=μ0u1,显然有μ0gt;1,且μ0u1=Au1≤T2u1.由于T2(P1)⊂P1,所以有

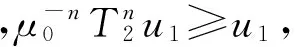
|n=1,2,…}⊂{u∈P1|u≥u1}.

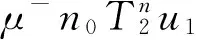
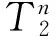
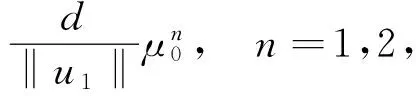
由Gelfand公式得

与r(T2)=1矛盾,所以假设不成立,因此

i(A,Br1∩P1,P1)=1.

(13)

由(12)式知存在εgt;0,使得f(u)≥(λ1+ε)u,其中u足够大.根据假设(H3),存在b≥0使得f(u)≥(λ1+ε)u-b,0≤ult;+∞.

取

r2=

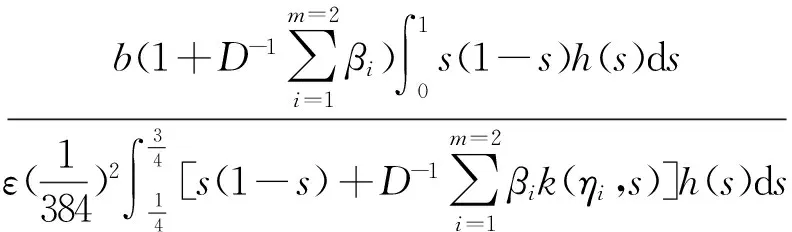
∀u∈∂Br2∩P1,

则有

(Au)(t)≥

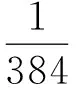
λ1(Tu)(t).

令u0是T关于λ1的正的特征函数,于是有u0=λ1Tu0,且

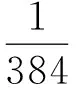
则有u0∈P1{θ}.

假设A在∂Br2∩P1上无不动点(否则结论成立).现证u-Au≠μu0,∀u∈∂Br2∩P1,μ≥0,否则,存在u2∈∂Br2∩P1,ρ0≥0,使得u2-Au2=ρ0u0,显然有ρ0gt;0,且u2=Au2+ρ0u0≥ρ0u0.令ρ*=sup{ρ|u2≥ρu0},则显然有ρ*≥ρ0gt;0,且u2≥ρ*u0.由于T(P1)⊂P1,所以有

λ1(Tu2)≥ρ*λ1(Tu0)=ρ*u0,

于是

u2=Au2+ρ0u≥λ1Tu2+ρ0u0≥

ρ*u0+ρ0u0,

此与ρ*的定义相矛盾,故假设不成立,所以u-Au≠μu0,因此

i(A,Br2∩P1,P1)=0.

(14)

由(13)和(14)式则知

i(A,Br2∩P1,P1)-i(A,Br1∩P1,P1)=

0-1=-1,

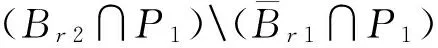
3 举例

例1考虑u(0)=u′(0)u″(0)=0,u″(1)=u″(1/3)+u″(1/9),h(t)=t-1,f(u)=2(36π)4e-uu,则

满足假设(H3).定义

显然有

因此

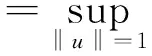
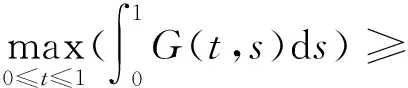
进一步可以得到

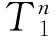
由Gelfand公式,则有

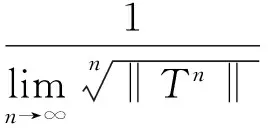
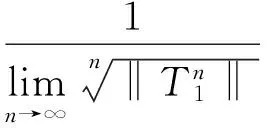
根据引理1,则知

因此

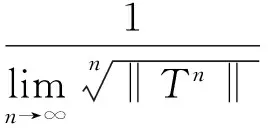
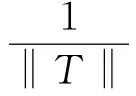
因为

2(36π)4gt;(36π)4gt;λ1,

0lt;1≤λ1.

根据定理1,则知四阶四点边值问题

至少有一个正解.

致谢大庆师范学院自然科学基金项目(12ZR10)对本文给予了资助,谨致谢意.

[1] 陆海霞,孙经先. 一类四阶非线性微分方程两点边值问题的正解[J]. 数学的实践与认识,2014,44(8):229-235.

[2] 卢整智,韩晓玲. 一类四阶两点边值问题多个正解的存在性[J]. 西南大学学报(自然科学版),2013,35(4):79-83.

[3] 吴红萍. 带两个参数的四阶边值问题的正解[J]. 西北师范大学学报(自然科学版),2014,50(6):16-19.

[4] 周韶林,吴红萍,韩晓玲. 一类四阶三点边值问题正解的存在性[J]. 四川大学学报(自然科学版),2014,51(1):11-15.

[5] 达举霞,韩晓玲,霍梅. 具有变号格林函数的四阶三点边值问题正解的存在性[J].吉林大学学报(理学版),2016,54(4):696-699.

[6] GRAEF J R, HENDERSON J, YANG B. Positive solutions to a foruth order three point boundary value problem[J]. Discrete and Continuous Dynamical,2009,285(3):269-275.

[7] PEI H R, SUN J P. Positive solutions for fourth-orderm-point nonhomogeneous boundary value problems[J]. J Appl Math Comput,2010,32(2):443-452.

[8] 李梦菲,李晓敏. 四阶奇异m点边值问题的正解[J]. 曲阜师范大学学报(自然科学版),2016,42(2):31-48.

[9] ZHANG G W, SUN J X. Positive solutions of point boundary value problems[J]. J Math Anal Appl,2004,291(2):406-418.

[10] GUO D J, LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones[M]. San Diego:Academic Press,1988:1-200.

[11] CUI Y J, ZOU Y M. Nontrivial solutions of singular superlinearm-point boundary value problems[J]. Appl Math Comput,2007,187(2):1256-1264.

[12] 王岩岩,崔艳艳,刘伟,等. 二阶脉冲微分方程三点边值问题[J]. 重庆师范大学学报(自然科学版),2015,32(2):64-67.

[13] 杨志春. Volterra型脉冲积分微分方程解的存在性和稳定性[J]. 重庆师范大学学报(自然科学版),2008,25(1):1-4.

2010MSC：34B18; 34G20

(编辑 郑月蓉)

Positive Solutions of m-point Boundary Value Problem for One Class of Fourth-order Differential Equation

ZHAO Wei

(DepartmentofTeachingEducation,DaqingNormalUniversity,Daqing163712,Heilongjiang)

The existence of positive solutions for the fourth-orderm-point boundary value problem

fourth-order equation;m-point boundary value problem; positive solution; cone; fixed point index

O175.8

A

1001-8395(2017)06-0791-06

10.3969/j.issn.1001-8395.2017.06.014

2016-12-25

黑龙江省青年科学基金(QC2009C99)和大庆市科技计划(szdfy-2015-63)

赵 微(1979—),女,副教授,主要从事非线性分析的研究,E-mail:zw-19791220@163.com