全国卷Ⅱ压轴题审题与巧解

集众家之所长，悟真题之精髓。

全国卷Ⅱ压轴题审题与巧解

高考题的最后一题(压轴题)一般情景比较复杂，意在考查学生的分析综合能力，因而难度大、分值高，而是否做对压轴题，则关系着考生是否能考上名牌大学。对于综合类试题，正确分析试题情境、领会命题人的思路是快速准确解答的前提；高考的考场时间宝贵，平时研究如何巧解压轴题具有十分重要的意义。下面以2017年全国卷Ⅱ第25题为例，结合多位一线优秀教师的智慧，从审题和巧解的角度深入分析。

【题目】如图1，两水平面(虚线)之间的距离为H，其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和-q(qgt;0)的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域，并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下；M在电场中做直线运动，刚离开电场时的动能为N刚离开电场时动能的1.5倍。不计空气阻力，重力加速度大小为g。求：

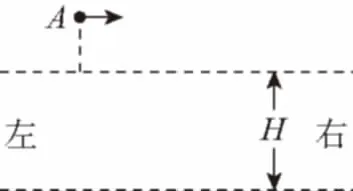
图1

(1)M与N在电场中沿水平方向的位移之比；

(2)A点距电场上边界的高度；

(3)该电场的电场强度大小。

【原解】(1)设小球M、N在A点速度大小为v0，则它们进入电场时的水平速度仍然为v0。M、N在电场中运动的时间t相等，电场力作用下产生的加速度沿水平方向，大小均为a，在电场中沿水平方向的位移分别为x2和x1。由题给条件和运动学公式得

v0-at=0 ①

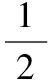
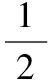
(2)设A点距电场上边界的高度为h，小球下落h时在竖直方向的分速度为vy，由运动学公式

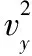
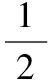
M进入电场后做直线运动，由几何关系知：

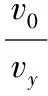
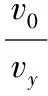
设M、N离开电场时的动能分别为Ek2、Ek1，由动能定理得

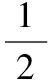
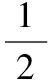
由已知条件Ek2=1.5Ek1

【陕西省永寿县中学孙冬子】理清思路，玩转高考题。

由于物理学科的抽象性、复杂性以及方法应用的灵活性，使绝大多数同学在学习中感到非常吃力，在遭遇一次次挫折后，越来越没了学习兴趣，从而使物理成绩越来越差，经过了解发现学生学习的主要问题是不能将所学物理知识应用于具体题目中，我认为此问题根源在于学生分析问题方法不当。物理解题的核心是对信息发掘、分析处理和应用，题目中的信息包含两类，一类是已知信息，也就是题干直接告诉的信息，另一类是隐含信息，隐含信息是在我们已掌握基本知识的基础上，结合题目所给的物理模型通过简单分析而获得的信息，当我们获得足够信息以后，再通过分析处理找出信息间的联系，最后用物理表达式反映出来，这样一步步去做就可以抽丝剥茧使我们的问题得到解决。

【发掘信息】①虚线间有水平向右的匀强电场

②质量相同、电性相反带电小球先后以相同初速度从A点水平抛出

③M在电场中做直线运动

④N离开电场时速度竖直向下

⑤M离开电场时的动能是N离开电场时动能的1.5倍

【信息分析】由①②分析可知，两小球从A点到电场上边界做平抛运动，且进入电场时具有相同的速度，进入电场后M、N水平方向受电场力大小相等方向相反，所以M、N水平方向分别做加速度大小相等的匀加速和匀减速直线运动，竖直方向只受重力，所以竖直方向M、N运动完全相同，因此两者穿过电场的时间相等。

由③知M进入电场后做匀变速直线运动。

由④知N进入电场后水平方向做匀减速直线运动，出电场时水平速度刚好减小到零。

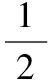
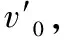
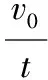
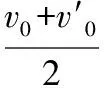
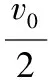
联立①②③得

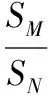
(2)由①式得M出电场时水平分速度为进电场时的2倍,由于M在电场中做匀变速直线运动,所以M出电场的竖直分速度也是进电场时的2倍,由于M在竖直方向做初速度为零的匀变速直线运动,所以小球M从A点运动到电场上边界的时间与小球通过电场的时间相等,设A点到电场上边界高度为h，则

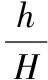
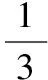
(3)设N出电场时速度为vn，M出电场时速度为vm，则

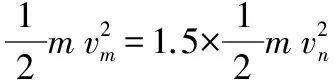
由动量定理可得：

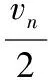
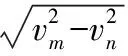
联立④⑤⑥式得:

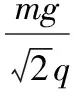
【点评】解题过程就是由已知量求未知量的过程，当已知量越多解题时的切入点就越多，所以解题时对信息的发掘非常重要，当然关于运动类题目，结合题意弄清楚物体的运动过程也至关重要。

【北京市丰台第二中学公衍录】巧分妙解，化难为易。

任何问题都有巧妙简单的求解方法，只有在平时学习时注意研究总结，才能在考试中拼出灵感的火花，找出巧妙简单的方法，从而节约宝贵的考场时间。正如同解放军战士训练的口号“平时多流汗、战时少流血”。

【第(2)问的巧妙解法】

方法1： 分解速度

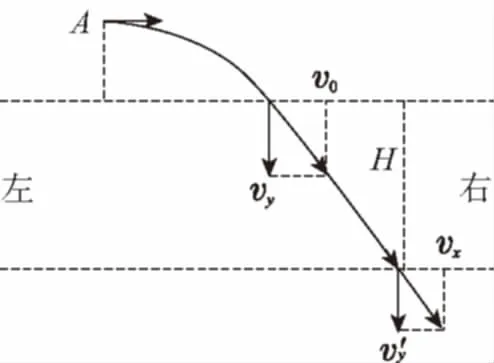
图2

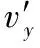
对M、N在电场中的水平分运动，由速度公式，M、N离开电场时的水平分速度分别为vx=v0+at，

0=v0-at，解得vx=2v0

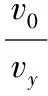
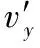
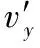
方法2： 分解速度 ，利用推论

方法3：分解速度和加速度

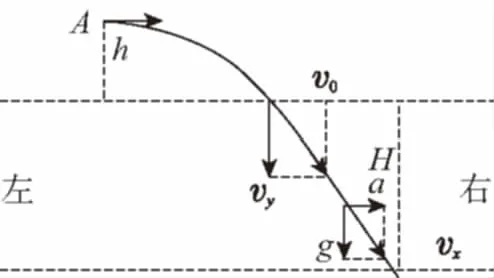
图3

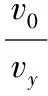
设M平抛的时间为t平，则vy=gt平。

再结合前面列出的③式0=v0-at，

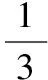
【第(3)问的巧妙解法】

1.全过程法

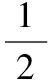
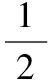
一般情况下，在全(整个)过程中列物理规律求解，往往比在分过程中分别列物理规律求解简单。

2.应用速度的分解与合成求解

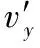
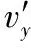
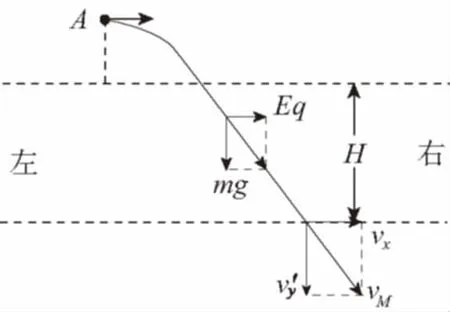
图4

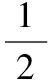
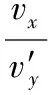
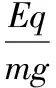
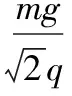
显然应用速度的分解与合成等求解第(3)问的方法非常巧妙简单。

【重庆市第三十七中学校段享冬杨天才】山重水复压轴题，柳暗花明图象法。

图象法思路更加清晰，解法更加简单，考试时用时也会较少，通常也是一些试题的“终极解法”。

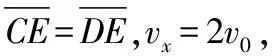
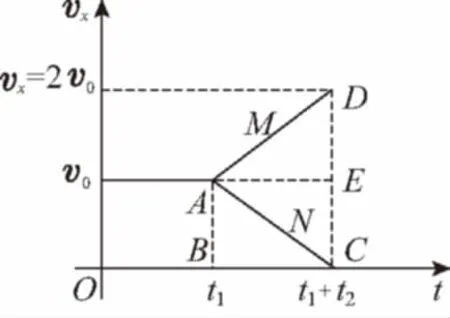
图5

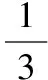
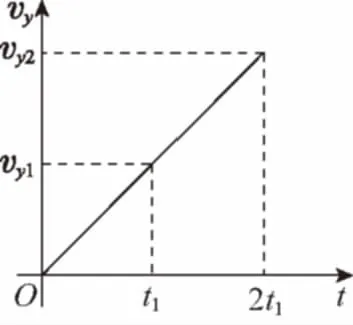
图6

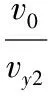
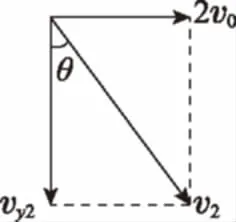
图7

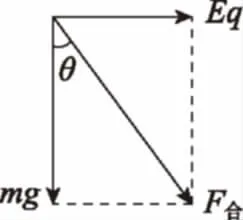
图8