利用加速度对斜面物体运动模型进行力学分析

浙江 厉 杰

邂逅加速度那一刻，便已柳暗花明。

利用加速度对斜面物体运动模型进行力学分析

在高中物理中，特别是高考模型里，斜面上的物体运动是一个非常重要的模型，常会在各省高考中出现，还会结合平抛、传送带、电场、磁场等其他模型一同出现。近年全国各地高考都以不同形式考查了这一模型。掌握这一基础模型，再由此拓展到与其他模型结合的题目，对于高中学生而言，显得尤为重要。

斜面上物体运动是一个范围非常广的模型，我们在这里要讨论的是如何用加速度去快速解决物体、斜面、地面三者间的作用力问题。

一、物体在斜面上处于平衡状态

【例1】(2013·北京卷第16题)如图1所示，倾角为θ、质量为M的斜面体静止在水平桌面上，质量为m的木块静止在斜面体上。下列结论正确的是

( )

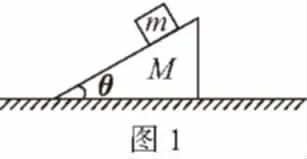
A.木块受到的摩擦力大小是mgcosθ

B.木块对斜面体的压力大小是mgsinθ

C.桌面对斜面体的摩擦力大小是mgsinθcosθ

D.桌面对斜面体的支持力大小是(M+m)g

【例2】(2011·海南卷第5题)如图2所示，粗糙的水平地面上有一斜劈，斜劈上一物块正在沿斜面以速度v匀速下滑，斜劈保持静止，则地面对斜劈的摩擦力

( )

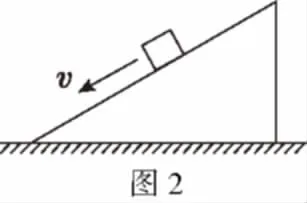
A．等于零

B．不为零，方向向右

C．不为零，方向向左

D．不为零，速度较大时向左，速度较小时向右

上面两道高考题的考点基本相同，都是研究斜面上物体处于平衡状态时物体、斜面、地面三者的受力情况。

解法一

物体受力分析如图3所示：

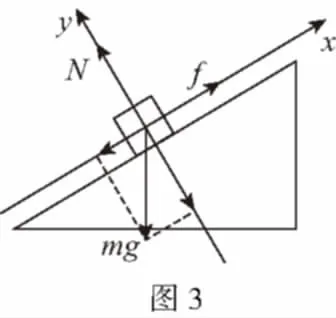
建立直角坐标系，对重力进行正交分解。可得：

f-mgsinθ=0

N-mgcosθ=0

同理：可以对斜面进行受力分析求解斜面和地面间的作用力。该种方法不是本文重点，不再展开。

解法二

我们试着在超重、失重知识的基础上进行推广，当系统或者系统中的某一部分拥有向上或者向下的加速度时，可以称这个系统处于超重或者失重状态，系统内的任一部分加速度都为零时，系统处于平衡状态。在两道题目里，物体与斜面组成的系统都处于平衡状态，无竖直方向的加速度，很快可以得出地面的支持力等于物体和斜面的重力之和。同理，地面摩擦力为零。(整体法)

故第一题选D，第二题选A。

上述方法对于斜面上不处于平衡状态的物体是否仍然适用？我们通过实例继续探讨这个方法的使用。

二、物体在斜面上处于非平衡态

对【例1】的延伸探讨

如图4所示，斜面体质量为M，倾角为θ，置于水平桌面上，当质量为m的小木块沿斜面体的光滑斜面自由下滑时，斜面体仍静止不动。则

( )

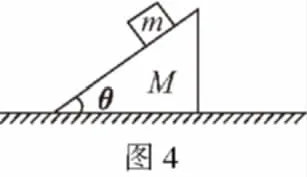
A．斜面体受桌面的支持力为Mg