基于Block-Bootstrap的银行内部评级系统区分力度量
(天津财经大学 经济学院,天津 300222)
基于Block-Bootstrap的银行内部评级系统区分力度量
刘久彪
(天津财经大学 经济学院,天津 300222)
内部评级法允许合格银行自行计算其资本要求,评级质量因而就显得至关重要。本文应用ROC曲线及其AUC量度检验评级系统的区分力,并针对多数银行违约数据不足和现有验证均假设违约独立的现实问题,引入Block-Bootstrap方法,在保持样本原有违约相关结构的同时,扩充检验样本规模;然后,通过具体实例计算、比较原样本与Block-Bootstrap方法扩充样本两种情况得出的评级系统ROC曲线和AUC量度值的准确性。
内部评级系统;区分力度量;Block-Bootstrap;ROC曲线
1 引言
一直以来,商业银行作为金融中介的核心竞争力都体现在其对所持信贷资产风险的有效管理,这也是它能够顺利度过经济衰退时期的根本保证。以前的信用风险评估只靠经验、直觉和少数专家的判断,而随着巴塞尔协议Ⅱ、Ⅲ的逐步实施,作为核心技术的内部评级法(IRB)正在成为国际领先银行进行信用风险管理的主流模式,其使用自己的信息数据、模型方法评估借款人的风险程度与规模,能够支持风险量化技术的客观化与标准化,但也衍生出评估判断失误的模型风险,美国次债危机已经清楚地表明了这一点。
为确保评级质量,巴塞尔委员会要求“使用内部评级法的银行必须定期对评级体系进行验证”,其中区分力度量是这一内部评级性能验证要求的最重要实现[1]。区分力是指评级区分履约人和违约人的能力,表征系统对借款人排序的正确程度[2]。区分力高代表系统预测为高信用等级的借款人未来基本不会发生违约,区分力低则意味着系统预测为高信用等级的借款人未来不一定不会发生违约。
现有的区分力度量方法大多假设拥有大量、稳定的统计样本和较多的违约观察值,但事实上:(1)真正具备长期经营记录、足够丰富历史数据的大型银行毕竟属于少数。(2)即使是大型银行,高质量信用组合的规模一般也比较小,这种组合可能多年没有发生过违约。(3)银行会根据累积的经验不断对评级系统进行修正,导致检验很可能使用的是过时的信息。简单的Bootstrap模拟虽然可以通过重复抽样扩大样本容量,却无法体现违约事件之间固有的相关性质[3],只有借助相关数据样本扩充的Block-Bootstrap方法能够同时实现上述两个目的,使对评级系统区分力的度量更为准确。
因此,本文针对多数银行违约数据不足和现有验证均假设违约独立的问题,立足于已有样本、特别是违约样本信息,且尽可能保持违约样本的固有相关结构,引入Block-Bootstrap方法扩充违约相关的样本容量,再应用已有的ROC曲线及其AUC量度检验评级系统的区分力,能够使得旨在增强风险管理能力的内部评级法具备更为广泛的适用性,推动绝大多数银行摆脱对外部评级和监管当局建议指标的依赖。
2 AUC区分力量度
内部评级系统区分力验证首先假设已对借款人进行了相应的风险评分,并观察到其一定时期(通常为一年)内的履约情况,据此计算能够表征该评级系统预测能力的统计量[4]。这一过程需要选择恰当的评分临界值,评分低于临界值为预测违约,高于为预测履约。但选取一个能被普遍接受的临界值基本上是不可能的,Soberart和Keenan将ROC曲线引入评级系统验证,使得银行可以通过不同评分临界值对评级系统的区分力进行度量[5],从而避免了为评级系统选择一个合适临界值的片面性,增加了评级系统区分力度量的科学性。
ROC曲线下面积(AUC)是为了直观考察ROC曲线对评级系统区分力的度量而提出的统计量,其代表评级系统对不同等级履约借款人和违约借款人的平均区分能力。在比较两个评级系统的区分力时,有时只观察ROC曲线并不能做到客观全面,AUC的比较可以更好地提升检验的准确性。
2.1 ROC曲线原理
原则上,内部评级系统在一个连续数值范围内产生样本内每个借款人的信用评分S,根据不同的评分临界值s可以对借款人做出两种预测分类,即高于s为预测履约N、低于s为预测违约D。为构造ROC曲线,按照信用评分从低到高对借款人进行排序,对于每个评分Si,评分小于等于Si的公司占所有公司的x%,评分小于等于Si的公司中实际违约公司占所有实际违约公司的y%,由此,每个信用评分Si决定一对数值(x%,y%),同时决定相应坐标系中的一个点,依次连结这些点,便可绘出ROC曲线。
ROC曲线通过描述履约借款人和违约借款人的分布对评级系统区分能力进行检验。本文5.3节图1中,对角线代表随机模型,因为随着评分的变化,违约人和履约人的分布是随机的,累积比例是相同的,此时的评级系统完全没有区分能力;完美模型的评级系统可以完美地区分违约人和履约人。但实际上,评级系统既不可能是完美模型,也不可能是随机模型,而是有一定的区分能力,体现为介于完美模型、随机模型中间的一条曲线,这条曲线越接近于左上角,评级系统的区分能力就越好。
2.2ROC曲线下面积AUC的计算
Stephen和Wei应用经验概率将AUC表示为[6]

(1)

(2)
其中nD代表样本中违约总体数量,nN代表样本中履约总体数量,SD和SN分别代表从违约总体和履约总体中随机抽取的信用评分。该公式为nD个SD和nN个SN相比较,如果前者小于后者,则比较的结果为1,相等时为0.5,大于时为0,即
(3)
将nD·nN个比较结果相加之后再取平均值,即可得AUC。
AUC是单位面积的一部分,因此其取值在0和1之间,其中随机模型的AUC等于0.5,完美模型的AUC等于1;实际应用中,任何合理的评级系统的AUC都应该在0.5和1之间,且数值越接近于1,ROC曲线越接近于左上角,评级系统的区分能力就越好。但需要注意的是,AUC作为一个一维量度值,只通过它是不能看出ROC曲线的基本形状和评级系统的区分力性质的,因此不能只观察AUC,还应注意ROC的形状。
3 违约事件的Block-Bootstrap模拟
度量评级系统的区分力,样本容量特别是违约样本的大小会显著影响最终结果。一般地,样本容量越大,模型区分力的检验也就越精确。但实践中,由于违约本质上是一种稀有事件,加之我国多数银行数据积累不足,可获得的样本数据很少[7]。统计学中的Bootstrap方法可对原始样本进行有放回的重复抽样以达到扩大样本容量的目的[8],但基本Bootstrap方法所基于的数据是独立同分布的,而违约事件之间具有明显的相关性,需借助Block-Bootstrap方法保持原有的相关结构[9]。
3.1Block-Bootstrap方法
Block-Bootstrap方法(块状自助法)是基于非独立数据进行的再抽样方法,为了保持样本数据的相关关系,不能对单个样本数据进行简单Bootstrap,需在再抽样过程中保证某一整块的样本数据放在一个集合中一起被抽取[10]。具体来说,Block-Bootstrap一般可按两种思路进行[11]:一种是重叠的块状自助法,即在划分组块时,各组块区间可以重叠;另一种是不重叠的块状自助法,即划分的各组块区间不是重叠的,其基本步骤如下:
(1)若是不重叠分组,需将原有的n个样本X1,X2,…,Xn按照一定顺序划分为Q块(组),每组的样本数据长度定为m,由此可以得到K1=(X1,…,Xm),K2=(Xm+1,…,X2m),…,KQ=(Xn-(Q-1)m+1,Xn-(Q-1)m+2,…,Xn); 若是重叠分组,每组的样本数据长度定为m,则会有n-m+1个分组,即为K1=(X1,…,Xm),K2=(X2,…,Xm+1),…,Kn-m+1=(Xn-m+1,…,Xn)。

(3)利用产生的块状自助样本X′计算未知参数θ的估计值θ′。
(4)多次重复步骤(2)和(3),可以获得多个块状自助样本、块状自助估计。
3.2 抽样块组长度的选取
对于Block-Bootstrap,确定合适的块组长度是至关重要的。如果块组长度过大,块状自助样本就和原始样本的区别不大,扩大样本容量的效果也就不明显;如果块组长度过小,违约事件之间的相关性质就不能很好地保留,也就降低了结果的准确性。Kreiss和Paparoditis对块状自助法的抽样块组长度选取得出了重要的结论[12]:在合理的假设条件下,对于数据间存在相关关系的样本而构造的统计量λ,其均方误差与样本的观察值之间成比例,可以通过对统计量λ的估计来确定块组样本的最佳长度,具体做法如下:
(1)给定块组长度的最初值m,通过数值模拟获得统计量λ(n,m)的估计值。
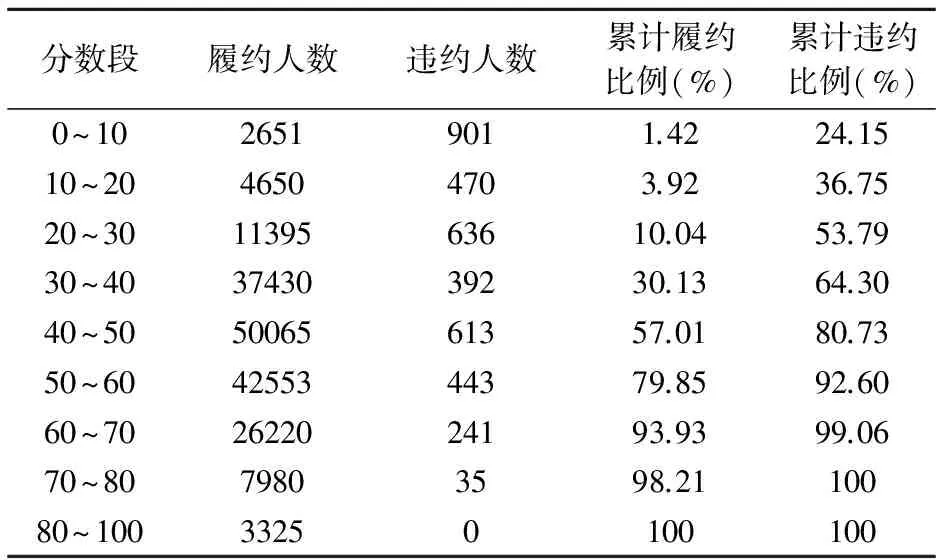
(2)选取分别满足g (4) 假设有n个借款人,内部评级系统计算出了他们各自的信用评分,观察其经过一段时间的违约结果,据此按评分从低到高的顺序计算各评分对应的累计履约借款人比例和累计违约借款人比例,进而绘制出ROC曲线。但由于实践中大部分借款人倾向于履约,违约事件出现的概率较小,通常无法描绘出准确的ROC曲线,这大大降低了以此为基础评价模型区分力的精确度。相比于简单Bootstrap,Block-Bootstrap扩大样本容量、提高违约事件出现的概率的同时,也能较好地考虑违约事件的相关性质,使ROC曲线的评价更为准确。 假设Xi(i=1,…,n)表示任意借款人i的违约指示变量,其有违约D和履约N两种可能结果,Block-Bootstrap绘制ROC曲线的步骤如下: (1)根据Raymond和Hukum的均方误差估计方法[13]确定该样本合适的抽样块组长度m。 (2)通过Block-Bootstrap扩大借款人样本容量: ①将借款人违约结果的随机样本X=(X1,X2,…,Xn)划分为n-m+1个块组Kt,其中t=1,…,n-m+1,每个块组中样本元素有所重叠,且每一组的样本数据长度都等于m。 ③重复步骤(2)T次,可以得到T个块状自助样本。 (3)按照信用评分由低到高的顺序对Block-Bootstrap产生的T×n=l(l>>n)个借款人进行排序,并将评分划分为w档,每档的评分上限定义为Sj(j=1,…,w)。 (4)观察一段时间后各借款人的履约结果,并计算每档信用评分中的履约样本人数nj,N和违约样本人数nj,D。 (5)对每个j=1,…,w,分别计算评分小于等于Sj的借款人占所有借款人的比例x%和评分小于等于Sj的违约借款人占所有违约借款人的比例y%,则此时由Sj决定的一组数值(x%,y%)可以决定坐标系中的一个点,依次连结这些点,即可绘出ROC曲线。 某商业银行为检验其内部评级系统中钢铁企业信用评级子系统F的评级质量,选择采用ROC曲线及其AUC量度评价该子系统的区分力。总结近5年的相关数据积累,将全部借款钢铁企业作为样本总体,从中得到可用于验证的建模外样本数量为2000个,其中违约借款企业总数为35个。 考虑到检验样本违约数量偏低,且相同行业企业之间具有较强的违约相关性质,需要利用Block-Bootstrap方法扩大样本容量后再绘制ROC曲线,以使区分力度量的结果更为合理和准确。下面基于原样本和Block-Bootstrap样本两种情况分别绘制评级子系统F的ROC曲线,计算AUC量度,并对其进行比较。 5.1 基于原样本的计算 (1)对2000个检验样本,首先应用评级子系统F计算每个企业在借款时的信用评分,按分数段(信用等级)统计检验样本总体的信用评分分布。 (2)借款企业的信用结果分为履约N和违约D两种,按照历史记录计算各分数段检验样本的累计履约比例和累计违约比例,结合信用评分分布如表1。 表1 基于原样本的信用评分分布 (3)根据上述数据绘制信用评级系统F区分力量度的ROC曲线。 (4)基于原样本的AUC计算。 对于表1中每一分数段(信用等级),根据检验样本履约数目SN、违约数目SD,分别计算检验样本违约总体中信用评分低于该分数段的样本数目y,进而根据下式计算每个分数段履约数目SN和违约数目SD的比较结果之和W (5) 进而可以计算基于原样本的AUC量度为 图1虚线可见,基于原样本的评级系统ROC曲线在低信用评分处较为平滑,也更靠近左上角;但在高信用评分处出现波动,并贴近对角线,近似于随机模型。同时,基于原样本计算的评级系统AUC量度值为0.25,这大大低于一个监管接受的评级系统AUC值应在0.5和1之间的标准。表面上,这些都将认定F不是一个合格的评级系统,其对信用水平较低的客户具有较高的区分能力,而对信用评分较高的客户几乎没有区分能力。 但是,仔细观察原样本的信用评分分布表1发现,ROC曲线呈现此种形状、AUC量度值偏低也可能是因为各分数段的检验样本数量偏少,造成严重的取样误差,这在高分数段的低违约情况下更易发生,从而不能准确评价评级系统的区分力,需要扩充样本容量重新进行检验,并比较结果综合判断。 5.2 基于Block-Bootstrap样本的计算 在样本容量不是很充足时,自助法可以充分利用已有信息显著扩充检验样本容量,块状可放回地抽取设计则能够保持违约事件之间固有的相关性质。据此获取一个Block-Bootstrap样本,重新绘制ROC曲线、计算AUC量度,并与之前结果进行比较、分析,可望对评级系统F做出更为合理的评价。 下面,对原样本利用块状自助法扩充样本容量,具体步骤如下: (1)按照Raymond和Hukum的思路[13],对于2000个原样本,以钢铁行业平均违约相关系数为标准,设定Block-Bootstrap初始数据块长度为2进行数值模拟,通过牛顿迭代法求得最优数据块长度为19。 (2)将2000个原样本随机排序编号,以相邻19个样本为一组,按编号顺序可重复地划分为1982个组块Ki,其中i=1,…,1982。 (4)根据评级系统F计算的每个样本在借款时的信用评分,得出Block-Bootstrap样本的信用评分分布,并按照历史记录计算各分数段的累计履约比例和累计违约比例,结合信用评分分布如表2。 表2 基于Block-Bootstrap样本的信用评分分布 (5)根据表2数据绘制Block-Bootstrap样本下的ROC曲线。 (6)根据前述计算方法,可以求得Block-Bootstrap样本下的AUC′为 5.3 原样本和Block-Bootstrap样本下的结果比较 将原样本和Block-Bootstrap样本下的ROC曲线放在同一图中比较如图1。实线表示随机模型的ROC曲线,虚线表示原样本下的ROC曲线,点划线表示Block-Bootstrap样本下的ROC曲线。 图1 原样本和Block-Bootstrap样本下的ROC曲线比较 由上可见,Block-Bootstrap样本下的ROC曲线相比原样本的情况更加平滑,低评分处和高评分处的区分力检验均未出现跳跃式的变化;同时,Block-Bootstrap样本下的AUC量度值为0.69,也在正常的取值范围之内。这都说明,简单地基于原样本认定评级系统F不是一个合格的评级系统是不够严谨、甚至是错误的,基于原样本的ROC曲线出现贴近对角线、近似于随机模型的波动,是因为其各分数段的检验样本、尤其是高分数段的违约样本数量偏少,造成严重的取样误差,从而不能准确评价评级系统的区分力;借助Block-Bootstrap方法扩充样本容量重新进行检验,能够得出更为科学、合理的评价结论。 由于违约本质上属于小概率事件,在检验样本并不十分充足时,若等待数据积累达到一定程度再进行内部评级建设会浪费许多时间和机会成本。 通过本文的研究: (1)借助Block-Bootstrap方法对原始样本进行分组块的有放回重复抽样,既可以充分利用已有样本、特别是违约样本信息达到扩大样本容量的目的,又能够保持违约样本的固有相关结构,满足内部评级区分力验证对检验样本数据的规模要求。 (2)传统的Bootstrap方法适用于独立同分布结构数据,而利用Block-Bootstrap进行分组块重复抽样,结合均方误差估计方法确定抽样块组长度,则可产生符合现实违约相关结构的检验样本数据。 (3)内部评级区分力验证过程中,ROC曲线及其AUC量度在检验样本、特别是违约样本偏少时,会出现严重的取样误差,从而不能准确评价评级系统的区分力;借助Block-Bootstrap方法扩充样本容量重新进行检验,则能够得出更为科学、合理的评价结论。 在美国次债危机引发全球金融海啸后,关于现代风险量化模型准确性的研究越来越受到重视,而以返回检验为主,综合各种预测决策技术对其进行管理的方法已成为这一领域的热点。内部评级是信用风险管理的基础和重大投资决策的依据,其技术水平直接关系着商业银行自身的安全发展。在国内,以工行、建行等为代表的大型商业银行也已纷纷启动了内部评级的研究开发工作。但与国际银行相比,我国银行数据积累普遍匮乏,特别是缺少已评级客户违约数据的历史统计,且规范性不够、数据质量不高,难以对评级结果进行合理的返回检验,从而限制了内部评级体系的发展和作用的发挥。本文研究有助于摆脱原有方法对统计样本规模的依赖,为数据稀缺的违约预测模型检验提供新的思路,从而建立起模拟检验内部评级模型的理论方法,对开展内部评级时间尚短的我国商业银行具有十分重要的实用价值,在内部评级模型开发、验证程序设计和平衡机制制定、风险管理策略选择等方面具有广阔的应用前景。 [1] Engelmann B. The basel Ⅱ risk parameters estimation validation and stress testing[M]. Berlin: Springer, 2012. 91-115. [2] 詹原瑞.银行内部评级的方法与实践[M].北京:中国金融出版社,2009.338-385. [3] 石庆炎,秦宛顺.个人信用评分模型及其应用[M].北京:中国方正出版社,2005.137-151. [4] Wolfgang A, Florian R, Gerhard W. Pitfalls and remedies in testing the calibration quality of rating systems[J]. Journal of Banking & Finance, 2011, 35(3): 698-708. [5] Soberart J, Keenan S. Measuring default accurately[J]. Risk, 2001, (8): 31-33. [6] Stephen S, Wei X. Analytic models of the ROC curve: applications to credit rating model validation[J]. A Volume in Quantitative Finance, 2008, (3): 113-133. [7] Tasche D. Estimating discriminatory power and PD curves when the number of defaults is small[J]. Journal of Mathematical Finance, 2010, (4): 1-58. [8] Davison A, Hinkley D. Bootstrap methods and their application[M]. New York: Cambridge University Press, 1997. 39- 45. [9] Dimitris N, Halbert W. Automatic block-length selection for the dependent bootstrap[J]. Econometric Reviews, 2004, 23(1): 53-70. [10] Jentsch C, Paparoditis E, Politis D. Block bootstrap theory for multivariate integrated and cointegrated processes[J]. Journal of Time, 2015, 36(3): 416- 441. [11] Hall P, Horowitz J, Jing B. On blocking rules for the block bootstrap with dependent data[J]. Biometrika, 1995, 82(3): 561-574. [12] Kreiss J, Paparoditis E. Bootstrap methods for dependent data: a review[J]. Journal of the Korean Statistical Society, 2011, 40(4): 357-378. [13] Raymond C, Hukum C. A random effect block bootstrap for clustered data[J]. Journal of Computational and Graphical Statistics, 2013, (2): 452- 470. MeasuringtheDiscriminatoryPowerofInternalRatingSystemsBasedontheBlock-BootstrapApproach LIU Jiu-biao (SchoolofEconomics,TianjinUniversityofFinance&Economics,Tianjin300222,China) The internal ratings-based approach allows the qualified banks to calculate their capital requirements on their own, so the quality of their rating is crucial. For solving the problems that the majority of banks don’t have sufficient default data and the existing verification are all assumed as independent default, this paper brings Block-Bootstrap approach to extend the sample size with maintaining the original default correlation structure. And then, it uses the ROC curve and its AUC to measure the discriminatory power of the internal rating system. Finally, the accuracy of the ROC curve and the AUC measurement of the internal rating system are obtained through an example calculation and comparison of the original samples and the Block-Bootstrap ones. internal rating systems; discriminatory power; Block-Bootstrap; ROC curve 2017- 02-14 教育部人文社会科学研究基金青年资助项目(12YJC790116) F830.33 A 1003-5192(2017)06- 0037- 06 10.11847/fj.36.6.37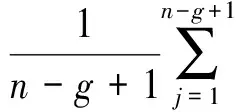

4 Block-Bootstrap违约样本的ROC曲线绘制

5 实例




6 结论与启示
——日晕

