渗透数学思想 培养中职生思维能力
黄玉莲
【摘 要】本文选取数形结合、转化思想、模型思想以及分类讨论这四种经典数学思想,探讨其对发展学生思维能力的作用。
【关键词】数学思想 思维能力 中职数学
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)09B-0132-02
在中职教育中,数学是一个基础性的课程,这门课也对学生的思维能力有着潜移默化的作用。在数学课堂上适当渗透数学思想,可以让中职生在知识能力和探究能力两个方面都更加完善。在中职的数学课堂上,学生面临的不仅仅是一道道的数学题目和解答,更重要的内容是如何领会其中的数学思想。只有通过问题看本质,才能深化思想、提升能力。
一、数形结合,探讨集合
数形结合思想是一种实用性非常强的数学思想,它不仅可以增强学生的实际分析问题的能力,而且可以更好地化解一些数学问题。“数”是指数字类的数学元素,而“形”则是具体的图形。说到图形,不仅是函数图象或者是几个图形,一条线、一个数轴即可称为一个图形。
以基础模块下册第一章《集合》为例。集合的概念对于学生来说是一个新的事物,将它放在第一章,说明了它是为了学生而打开新世界的大门。集合是一种简单但是却很重要的一个数学概念,在命题真假判断、排列组合、函数值域等方面有着极其重要的应用。集合就是某一类数的组合体,属于数字类的数学元素,在大多数情况下采用“数”逻辑来运算。集合通常用“{a1,a2,a3,…}”这样的形式来表示,“数”的属性很强。但是在解题过程中,数字给人的感觉是抽象的,需要动脑进行分析,而且耗费时间较多。换个角度思考,如果数字运算不简便,那么我们可以由“数”延伸至“形”。形可以使数变得更加直观,数也可以为形增添精确性。此时,数形结合是解题的关键。例如下面一道题目: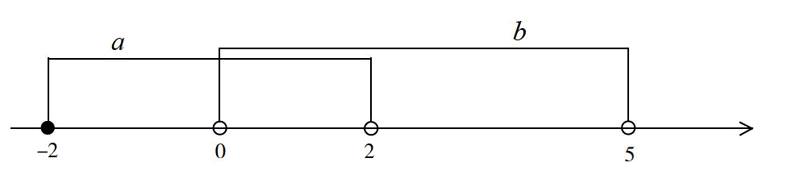
已知 ,,求 a∩b。
其实这是一道简单的题目,但是如果运用数轴的方法可以让这道题目更直观。当参与交集的集合增多时,数形结合的数轴法就显出了它的优势。以这道题为例,如果将 a 和 b 两个集合画在数轴上时,如图 1 所示,那么我们就可以轻易地观察到,a 与 b 的交集,或者说 a 与 b 的公共部分,就是中间的那一块区域,也就是 {x|0 集合在大多数情况下是数的集合,但是这并不意味着只能用“数”的思维去解决问题。在数字运算中引入“形”的方法,数形结合方能灵活解题。数形结合不只是一种解题策略,更是一种深入人心的数学思维方法。 二、多元转化,变换方程 转化思想也是一种经典的数学思想。学习数学的最终目的就是运用恰当的数学工具解决数学问题,因此不管采用哪种思路,只要能够把问题解决,就是好思路。在解决问题中,采取间接的方式、采用转化的思想,也不失为一种明智的策略。 数学是一门灵活的学科,一条路走到黑是行不通的。转化思想就是一个很好的例子,这里采用第二章《不等式》的知识进行说明。举一个实际的题目: 解不等式 学生看到分式,可能很多就要皱眉头了,因为分式的通分比较麻烦。但是对于这道题目来说,学生看到分式就发愁还有点为时过早,因为不等式的右侧是个“0”。因为 0 的存在,我们就可以将不等式进行转化,比值大于 0 则说明分子、分母是同号的,也就是它们的乘积也大于 0。那么原式即可转化为:,不等式一下子就简单了很多。运用转化思想最重要的原则就是等价关系,但是上述转化是不等价的,还缺一个“x≠1”的条件。细心、灵活,是运用转化思想的要领。 通过转化不等式的案例,学生可以从中看到转化思想的力量。转化的意义在于简化问题。但是世上没有免费的午餐,简化问题也有代价,那就是需要付出思考,并且承担着转化不等价的风险。 三、建立模型,引入函数 数学是自然规律的一种反映形式,本质上来说就是一种模型。建立数学模型是解决问题的首要一步。在解决一些实际化的问题时,首先需要建立一个数学模型,引入一些数学工具。建立模型的过程实质上是分析问题的过程,它对解决问题起到举足轻重的作用。 以第四章《指数函数与对数函数》为例。指数函数是中职数学中新学的一种函数,在运算方面具有一定的难度。从实际生活上来讲,很多生活中的问题与指数函数息息相关。理论知识与实际应用之间的转化,这就是建立模型的过程。以一个具体的题目为例: 在一个施工工地上,有一台挖掘机,价值 40 万元。随着时间的流逝,它的价值会降低,每一年比上一年的折旧率是 20%,问当它的价值折旧到 30 万时所用的时间。 面对这道题目,我们要采用试验的方法来建立模型。当使用 1 年时,设备价值为 40×(1-20%)万元;当使用 2 年时,设备价值为 40×(1-20%)×(1-20%)=40×(1-20%)2 万元。如此一来,那么这一数学模型即为对数函数,可以设 x 年后,这台挖掘机价值为 30 万元,列出方程式为 40×(1-20%)x=30,然后用计算器即可解出最终结果。数学模型有很多种形式,可以是函数也可以是图形,但是不论什么形式都是为解决问题而生的。通过建立数学模型,简便解题,是数学思想的彰显。 四、分类讨论,明确数列 数学的一种经典方法就是归纳,也就是将不同的问题用相同的规律进行表达,从而简化解题过程。但是在某些情况下,归纳到一起并不容易,甚至不利于问题的解决,那么这时候就不能强行进行归纳,而是需要采用分类讨论的思想,先分后合。 以第六章《数列》为例,数列的题目可谓是变化万千,学生在解题时,可能会遇到各种各样的分类情况。如何恰当地分类讨论,并且能将不同的情况合理地归纳起来,可以说是数列题目中永远的难题。引用一道比较经典的例题进行探究: 已知一个等比数列 {an} 的公比为 q,数列的前 n 项和 Sn>0(n=1,2,3,…,n),根据上述条件,求公比 q 的取值范围。 这是一道非常经典的等比数列问题,规律也比较普遍。在本题中对 q 的取值范围没有任何说明,进行分类讨论势在必行。首先由前 n 项和 Sn>0,q≠0,可以推得 a1=S1>0。分类讨论的原则是先讨论简单的、特殊的情况。从解题难度上讲,先讨论特殊情况,将问题的范围缩小,然后再进一步进行推导;从考试得分上讲,先写出简单部分有利于先行获取应得的分数。在数列中,特殊情况就是公比或者公差特殊的情况。首先需要考虑 q=1 的情况,当 q=1 时,Sn=na1>0,显然 q=1 的条件下,是符合题目要求的。在 q 不等于 1 的情况下,,化简可得 ,(n=1,2,3,…),等价于 1-q<0,1-qn<0 或 1-q>0,1-qn>0。对上述式子进行求解,可以得出 q>1 或 q<1 且 q≠0。这只是一个简单的例子,当学生面对数列问题时,一定要有这种分类讨论的思想。 数列问题中的分类讨论是一种典型的解题思路,当然在其他类型的題目中,分类讨论也是一种重要的方法。任何的思想都没有普适性,因此需要因题制宜,灵活运用。借分类讨论思想,可以明确数列的性质特点,提升能力。 总而言之,数学思想渗透在数学问题中的方方面面,一个小的技巧、一个简单的方法中都会彰显着数学思想。数学思想是属于一种深邃的、高阶的数学能力,学生在培养数学思想的过程中,需要付出很多的努力,需要在实践中不断提升、不断总结。 【参考文献】 [1]徐志成,管毓红.数学思想方法及其在高中、中职数学教学中的应用[J].中国培训,2016(5) [2]郑 洁.中职教育中数学思想方法的渗透[J].法制与经济,2010(8) [3]张 亚.数学思想方法在中职教学中的运用[J].辽宁教育行政学院学报,2009(2)

