加强空间感知 提升想象能力

江苏省南京市行知实验中学 徐 敏

加强空间感知 提升想象能力

江苏省南京市行知实验中学 徐 敏

空间几何是中学数学的重点，其着重培养了学生的空间想象能力，也是核心素养之一——直观想象素养最有效的体现。加强空间感知教学，有助于提高学生的想象能力，也为其头脑中建立空间概念奠定基础。

立体几何；数学；空间感知；直观想象；空间想象能力

众所周知，直观想象素养是数学课程标准提出的六大核心素养之一，其要求学生通过几何直观培养想象能力。在传统的公理化体系下的欧式几何中，四大公理托起了整个立体几何的大厦，让我们的空间认知全部建立在这个公理之上，从而形成了空间想象能力。但是近年来，因为空间向量的引入已经大大降低了学生对于立体几何空间感知的依赖性，在一定程度上降低了思维的难度，也降低了思维的乐趣。笔者认为，空间向量的确可以解决空间几何问题，但是过于使用其代数化的本质而疏远了几何特征，从而降低了思维含量，这也在近年的高考试卷中体现出命题不断向传统公理化方式倾斜，以求不同方法的公正性。

一、三视图注重感知

三视图是空间几何初学的必备知识，三视图将一个完整的空间几何结构体用平面图形完整地展示出来，其具备了空间几何平面化的基本思路。对于学生而言，特别是偏文类的学生，其头脑中基本感知模型欠缺，造成了认知的不足。教学中建议以基本图形为主，辅以平面和空间的转换，加强空间感知，提升想象能力。

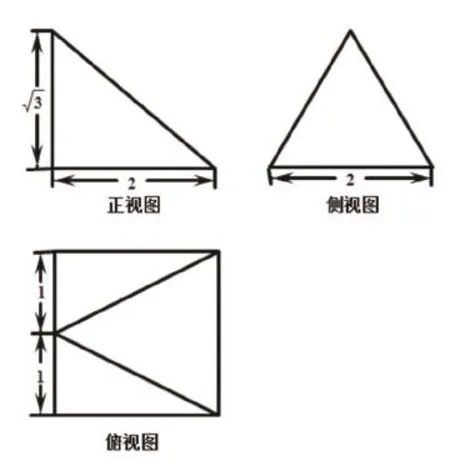
分析：本题是容易题，初学者对其的认知尚不具备完整的想象，教学建议从某一图形出发，辅以其他视图进行，以提高空间感知。观测俯视图可知，底面图形以正方形为研究对象，辅以正视图中的垂线和侧视图中的等腰形态，不难发现其原几何体结构是四棱锥，问题迎刃而解。

二、对定理的理解运用

空间几何传统解决方案中，四大公理是立体几何大厦的基本，而后平行垂直的八大定理则是空间几何传统大厦的支柱。要培养空间感知，恰恰是从各种图形结构中获取定理使用的情境，以模型为载体，抽象出定理使用的基本，从而获取空间想象能力。

问题2：在三棱柱ABC-A1B1C1中，△ABC是正三角形，且A1A=AB，顶点A1在底面ABC上的射影是△ABC的中心。（1）求证：AA1⊥BC；（2）求直线A1B与平面BCC1B1所成角的大小。

分析：斜棱柱的解决是学生提升空间想象能力的关键。对于本题涉及的斜三棱柱来说，我们最想去寻找的依旧是存在于几何结构体中的线面垂直，思考本题不难发现，射影恰恰是一种线面垂直。有了这样的依托，要解决第（1）问自然

水到渠成。设O为△ABC的中心，连接AO，所以BC⊥AO，又AA1⊥BC，所以BC⊥面A1AO，因此BC⊥A1A。

对于第（2）问来说，研究线面角是传统几何的常态，也是热点问题。从公理化体系的解决方式中，我们一般使用两种方式，其一是获取斜线在平面中的射影，这一般需要找到线面垂直作为支撑；其二是利用等体积法获取高度。观察本题斜三棱柱，因为有第（1）小题的线面垂直支撑，所以从第一种传统方式入手思考更便捷。取BC、B1C1的中点E、F，连接AE、A1F、EF。由（1）知BC⊥面A1AEF，从而面A1AEF⊥面C1CBB1，在面A1AEF内作A1G⊥EF，垂直为G，连接GB，则∠A1BG是直线A1B与平面B1BCC1所成的角。设A1A=2，在平行四边形A1AEF中，

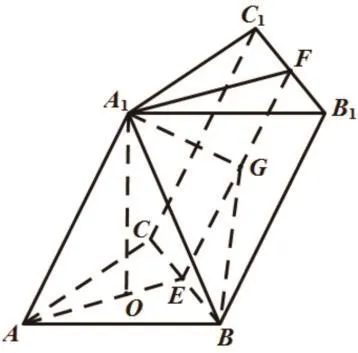
本题的线面角求解过程中的“找——证——算”是典型的传统方案，对于学生而言，最困难的是找！线面角在传统方法中怎么寻找？前面已经讲述了两种常用方式，就第一种方式而言，找到线面垂直的方法又具备一定的模式化：一般来说，往往找斜线与面中某一直线垂直，进而转化为证明面的垂线。教师还要对学生加以合理的命题意图的引导：一般这种垂直往往在某些线上，不太可能在“荒郊野岭”，这就鼓励学生大胆往特殊位置上尝试，从空间感知来讲，这样的位置是可以实现的。将线面垂直的判定定理运用到具体情境中，体现了定理与现实抽象的结合，实现了想象能力的提高。

总之，加强空间几何教学需要进一步加强传统方式的教学，这是因为传统方式提升了学生的空间感知，笔者建议教学首先还是需要关注传统方式，而空间向量始终适宜作为传统公理化教学的补充，这样的方式才有助于培养具备合理空间想象能力的学生，从而获得直观想象的素养。

[1]沈恒.浙江七年高考立体几何自主命题回顾与前瞻[J].数学通讯，2010（10）.

[2]薛彬.高中立体几何改革的回顾与前瞻[J].中学数学教学参考（上旬），2014（3）.

[3]戴海林.立体几何教学中的转化策略——15年高考阅卷随想[J].中学数学月刊，2015（11）.