运用数学思想方法，打开解题思路

浙江省义乌市廿三里第二小学 戴莹婷

运用数学思想方法，打开解题思路

浙江省义乌市廿三里第二小学 戴莹婷

如何寻求解题思路，提高学生分析问题和解决问题的能力是目前教学方面的重难点。本文通过对具体问题进行进一步分析，以数学方法为指导，在加深对数学思想方法的理解基础上，应用解决问题策略打开解题思路，提高学生分析问题能力。

思想方法；解题思路；策略

数学思想方法是解决数学问题所采用的方法。它是数学概念的建立、数学规律的归纳、数学知识的掌握和数学问题解决的基础。《小学数学课程标准》指出：面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻求解决问题的策略。在日常教学中，利用列表、假设、转化、逆推、简化等策略，进一步提高学生发现问题、分析问题、解决问题的能力。那么，在小学数学教学当中，该如何运用这些策略来解决数学问题呢？

一、观察列表，分析问题

列表策略，作为学生发现问题和进行整理分析的具体教学策略被广泛应用。在进行列表教学的过程中，首先从所得数据信息展开教学，从数据之间的量化关系作为切入点，带动学生发现问题；其次，根据一定的规律对数据进行整理，让学生学会利用表格将这些信息进行汇总分析，并得出相关规律，从而解决问题，培养出利用表格策略的数学思维方式和解决问题的能力。如今有很多为了提高学生分析和解决问题的能力所出的关于列表方面的题目，例如：三年级有三个班，各个班信息数据如下表所示，根据表格信息解决以下问题：（1）求二班女生人数；（2）求三班男生人数；（3）求三年级总人数。

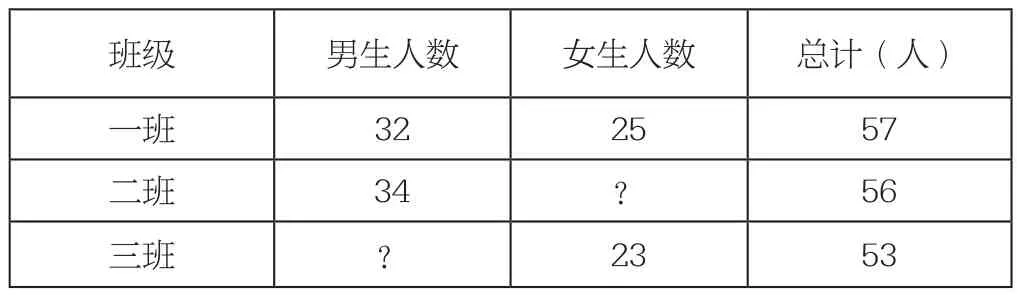
三年级各班人数信息（表）

在讲解这类题目之前，先要引导学生进行独立思考，然后教师再进行提问：同学们从这个表格中得出了哪些数学信息？通过分析，发现其中所隐藏的信息，也就是利用列表策略使学生形成能够发现问题和主要信息的惯性思维模式，然后通过自己分析的信息进行合理的解答。在今后的学习生活中，可以首先分析问题的信息数据，然后进行整理得到所需的主要信息，并且分析与其他内容的相关性，这种列表策略转化的数学思想方法打开了学生思路，同时也能够帮助学生更好地解决问题。

二、通过假设，进行推理

对于一些复杂并难以解决的问题，可以利用假设的数学思想方法解决遇到的问题。让学生在应用假设法过程中形成数学思维方式并进行推理，学会对假设结果进行验证，形成严谨的解题模式。

我们可以从一些假设出发，促进学生更深刻的理解假设。比如，可以出一些题目让学生自主讨论分析。著名的假设例题鸡兔同笼：鸡兔共有38个头，88只脚，鸡兔各有多少只？组织学生进行小组讨论，提出解决的方案，然后根据这几种不同的方案展开假设，进行结果的对比总结，代入进行比较，选出最准确的答案。还可以将课本中的例题提出一起讨论，让学生加深理解。通过创造这种假设例题的模式，使学生学会分析问题，提出假设，并且根据小组的不同思想进行合理调整。利用这种假设策略解决问题的过程，可以锻炼学生的推理能力，课后可布置习题让学生自己进行推理假设，巩固假设思想，提高对学科的学习兴趣，从而打开解题思路。

三、合理转化，化难为易

在数学教学当中，要培养学生通过转化思维转化打开解题思路，并通过掌握基础转化模式解决问题，巩固转化数学思想模式，并应用于解决其他问题。

例如：在多个正方形累计的格子中附上两种不同形状的图形，如何证明其面积相等？可以通过提出问题，让学生进行讨论分析，进行不同的拼装组合，证明是否相等。这种转化策略，可以从各方面进行考虑，比如将其进行转移、角度旋转等。又如在进行分数除法计算时，分数乘法进行运算。利用这种转化策略的数学思想方法，使学生从多方面进行思考，拓展思维，打开解题思路，在一定程度上将困难问题简单化，从而更易于解决问题。

四、运用逆推，发散思维

逆推的数学思想方法是解决问题中最重要且运用最多的一种思维方式。此策略对学生的学习目标内容分为以下几类：学会利用逆推的方式打开解题思路；掌握逆推的基础模式并用于解决问题；增加学生推理思维能力，解决其他复杂问题。

一般来说，逆推的过程是从结果开始一步步推理，从而得出答案的过程。例如：某学生从家出发经过超市、公园到达学校；从学校到家又走另一条路，从学校到体育广场，然后经过电影院到家，其中电影院可以到达公园，计算此学生从学校回到家的最短路程。从这个问题可以分析从学校到家的几条路，分别比较路程的距离，然后得出最后的结果。这便是逆推策略的具体实例表现，可以利用这种数学思想方法拓展学生的思维，从多角度进行考虑，形成自行思考推理的思维模式，从而打开学生的解题思路。

五、有效简化，清晰思路

简化问题虽然对解决问题具有重要作用，但是在简化复杂问题时还是具有一定的复杂性。学会将复杂问题简单化的数学思想方法；学会剖析，抓住重点并解决问题，此两点是简化策略的具体实施目的。

根据问题的具体信息抓住其中的重点，然后将问题简化，从而进行简化分析，解题思路会更加清晰。例如已知：2、4、8、16、32……，求第10个数字是多少？针对此类型的例题展开讨论，首先得出数字排列规律：21,22,23,24,25，…，那么第10个数字则为210，从而将复杂的题目简单化解决。利用这种简化的策略，首先根据题目的具体信息进行重点的提取，然后建立新的模型进行再次分析，不过应用的方式为学生所熟知的方式，利用简化策略的数学思想方法，提高学生对问题的理解分析能力，从而使其对解题产生兴趣，进一步打开解题思路。

六、数形结合，理清关系

引导学生学会使用数形结合思想，会在很多类型题的解题里有较大应用。数形结合对学生的几何思维和逻辑思维构造也有很大帮助，让学生能够勤于动手，将抽象的数字进一步转化，以图形的形式表现出来。

因此，根据题中所给出的各个条件之间的关系分析，将关系以具体的形式表现出来。比如：甲和乙行驶相同的距离，甲的速度是乙的两倍，甲在到达终点后返回，求与乙相遇时要多久？在这种应用题中，涉及了甲、乙速度和时间的关系，还包括相遇追及的问题。解析这类题最有效的方式便是画图，将两者所经历的路程关系在图中表现出来，先画一条线段表示全长，甲所跑的路程是全长线段如上返回相遇的路程，而乙所跑的路程是从出发到与甲相遇的路程。这样，我们就可以很直观地看出甲所跑的距离是一个全长加上乙距离全长的距离，由此建立等式，通过设未知数等方式进一步得出结果。

在数形结合的转化策略中，最主要的优势是可以替学生理清题中所给出的各个条件关系，让学生能够清楚地利用已知条件展开解题，且在建立了等式的基础上也能对各个数据有更加全面的把握，还可防止有考虑未全面的地方。多画图对学生思维能力的培养也有很大帮助。

总之，在小学数学教学中，我们要充分将公式、法则、定义与思路分析相结合，打开解题思路，使学生创造力得以培养。