例析非特殊角的表达与运算
■浙江省天台中学高三︵2︶班 陈叶晨︵指导教师:褚人统︶
在中学数学课本中出现的角大多是与30°,45°,60°相关(成整数倍)的特殊角,要想表达与运算非特殊角,我们该怎么做呢?下面我们就来谈谈这个问题。
在中学数学运算里出现的角α,从使用频率来看有两类,一类是“特殊角”,另一类是“非特殊角”。所谓α是特殊角,就是指可以通过三角函数的诱导公式,把α化为30°、45°、60°或其倍数的角,或者化为15°、18°或其倍数的角,它们中的每一个角的三角函数值不用查表,都可以通过使用三角公式运算确定出来。上述之外的角,我们都称为非特殊角,对于这些角,一般要通过查表,方可以得到它们的三角函数值(近似)。
在高考中,非特殊角的表达与运算也与特殊角一样重要。在一个特定时段内,以点E为中心的7nmile以内海域被设为警戒水域。点E正北55nmile处有一个雷达观测站A。某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距402nmile的位置B,经过40min又测得该船已行驶到点A与点A相距1013nmile的位置C。
(Ⅰ)求该船的行驶速度(单位:nmile/h)。
(Ⅱ)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由。


(Ⅱ)方法一:如图1所示,以A为原点建立平面直角坐标系,则B(40,40),设点C的坐标分别是(x2,y2),BC与x轴的交点为D。x2=ACcos ∠CAD =1013cos(45°-θ)=30,y2=ACsin ∠CAD =1013sin(45°-θ)=20,所以过点B、C的直线l的,直线l的方程为y=2x-40。又点E(0,-55)到直线l的距离=35<7,所以船会进入警戒水域。
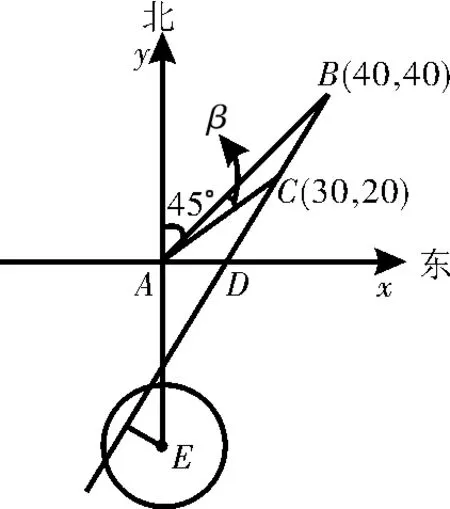
图1

图2
方法二:如图2所示,设直线AE与BC的延长线相交于点Q。在△ABC中,由余弦定理得在△ABQ中,由正弦定AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=15。过点E作EP⊥BC于点P,则EP为点E到直线BC的距离。在Rt△QPE中,PE=QE·sin∠PQE=QE·sin∠AQC=QE·sin(45°- ∠ABC)=,所以船会进入警戒水域。评注:题目中对θ是用“其中sinθ=表达的,是常用的表达方式,这里要理解θ是确定的锐角且正弦值为
如果遇到将特殊角隐藏在函数中的问题时,需要仔细识别,从中发现非特殊角运算的特点,以及与特殊角运算的区别等。




图3
评注:在非特殊角的表达、转换、运算时,我们务必要注意:(1)对于非特殊角,我们要根据它的条件范围及三角函数值准确判断它的更小范围,这个范围越小越好;(2)有非特殊角参与的运算大多数是需要使用公式asin x+bcosx=Asin(x+θ)的,变形主要是左右互化,这里的θ就是确定的、已知的非特殊角。

