具有时滞和治疗的丙肝模型分析

张丽婷，冯 飞，董亚丽，乔志琴

(中北大学理学院，山西太原 030051)

具有时滞和治疗的丙肝模型分析

张丽婷，冯 飞，董亚丽，乔志琴

(中北大学理学院，山西太原 030051)

为了进一步研究丙型肝炎病毒的传播机理及其治疗的有效方法，针对丙型肝炎病毒潜伏期比较长，且在整个患病期内均具有传染性的特性，在已有的模型基础上引入时滞来反映丙肝潜伏期的存在。为研究时滞和药物治疗对丙肝传染病的影响，建立了具有常数输入和时滞的丙肝传染病模型，利用常微分方程定性理论知识分析其对应平衡点的存在，构造Liapunov函数讨论无病平衡点的全局稳定性，并且分析了时滞对系统的影响。通过分析可知，当时滞大于零且基本再生数小于1时，系统在无病平衡点处是全局渐近稳定的。给出了正平衡点稳定、不稳定与系统产生Hopf分支分别对应的前提条件，通过对阈值的分析给出了控制丙肝传播的措施建议。数值模拟验证了结果的正确性，其结果对具有时滞和治疗的丙肝模型的研究是有意义的，可为减少丙肝的流行提供新的思路。

稳定性理论；丙肝；时滞；治疗；Hopf分支

丙肝是由丙型肝炎病毒感染所引起的疾病，其传染性很强，感染后很难治愈，且极容易转化为慢性肝炎，还有可能发生肝硬化及诱发肝癌。在医学上，丙肝分为急性丙肝和慢性丙肝，两者的早期症状都不太明显，很容易被忽视，国内外至今也没有可以有效预防丙肝的疫苗和治疗方案，病毒感染者只能通过干扰素和利巴韦林联合治疗。

很多学者已经通过建立传染病模型对丙肝进行研究，如MARTCHEVA等在文献[1]中考虑了人口变化这一因素，并且引入慢性感染，建立了一个SIS模型；KRETZSCHMAR等在文献[2]中研究注射毒品者之间的丙肝传染情况；在文献[3—4]中，研究者阐述了由于免疫力减弱，恢复者可能再次成为易感者，并建立了SIRS模型；有研究人员指出有效治疗在一定程度上可以阻止丙肝继续传播及再次感染[5]；ELBASHA在文献[6]中分析了抗病毒治疗的重要性；NAZARI等[7]考虑了丙肝的再次感染会产生后向分支。由于丙肝具有2～26周的潜伏期，且在整个患病期内均具有传染性，故SUN等在文献[8]中引入潜伏期，建立了SEIR模型，目前，由于研究的深入以及现实存在的问题，研究者对于时滞的应用越来越广泛[9-13]。

本研究在已有研究的基础上引入时滞来反映丙肝潜伏期的存在，将总人口作为研究对象，总人群分为易感者S，染病者I，治疗者T，恢复者R。建立的仓室图如图1所示。

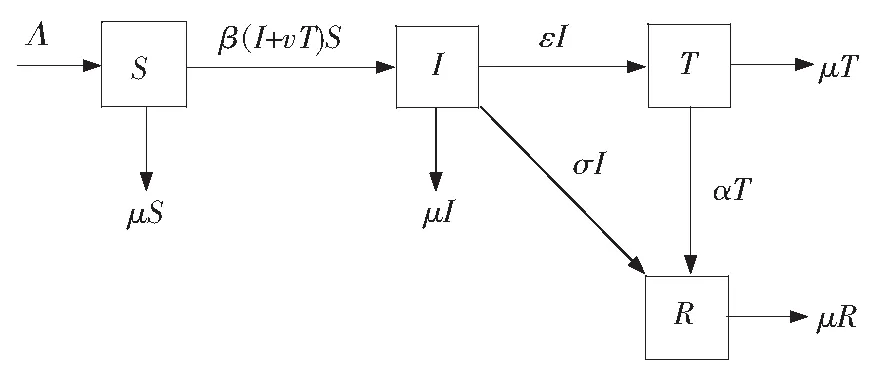
图1 仓室图Fig.1 Warehouse map

其对应的数学模型为

(1)

式(1)中，参数Λ>0是人口的输入率，μ>0是自然死亡率，β>0是易感者与染病者的接触率，ε>0 是染病者的治疗率，σ>0是染病者的恢复率，α>0是治疗者的恢复率，v>0是治疗者较染病者的相对传染性。总人数的变化满足：

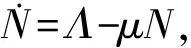
故

引理封闭集合：

是正不变集，且对模型中的所有正解都吸引。

1 无病平衡点分析

考虑模型(1)无病平衡点

的稳定性。R表示基本再生数，用定义求得:

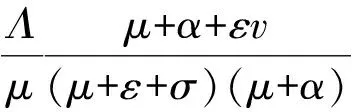
模型(1)在E0处的雅克比矩阵如下：

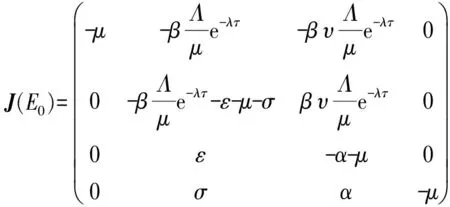
(2)

其特征根满足方程：(λ+μ)2(λ2+A1λ+A2)=0,显然，其对应的特征值有2个，均为-μ<0,而其他2个特征根满足方程：

λ2+A1λ+A2=0。

(3)

当时滞τ=0时，有如下定理。

定理1当R<1时，系统在无病平衡点E0处是局部渐近稳定的；当R>1时，系统在无病平衡点E0处不稳定。

当时滞τ>0，式(3)可以改写为

λ2+(2μ+α+ε+σ)λ+(μ+α)(μ+ε+σ)=

(4)

定理2对任意的时滞τ>0,当R<1时，系统的特征根均具有负实部，故E0局部渐近稳定；当R>1时，E0不稳定。

证明令

F(λ)=

λ2+(2μ+α+ε+σ)λ+(μ+α)(μ+ε+σ),

显然，当R>1时，G(0)>F(0)，此时式(4)必然有1个正根，故E0不稳定；反之，当R<1时，G(0)0上单调递增，G(λ)在λ>0上单调递减，此时上式没有正实根，假如其有非负实部，则必须为虚数。

假设λ=iω(ω>0)为方程的根，则

-ω2+(2μ+α+ε+σ)iω+(μ+α)(μ+ε+σ)=

分离实虚部有：

-ω2+C=Aωsinωτ+Bcosωτ，

Dω=Aωcosωτ-Bsinωτ,

其中：

C=(μ+α)(μ+ε+σ),

D=2μ+α+ε+σ。

平方后相加有：

ω4+(D2-A2-2C)ω2+C2-B2=0,

令ψ=ω2,则ψ2+(D2-A2-2C)ψ+C2-B2=0。反之，当R<1时，D2-A2-2C>0,C2-B2>0,则没有这样的ω, 使iω满足式(4)。

定理3当时滞τ>0且R<1时，系统在E0处是全局渐近稳定的。

证明构造Liapunov函数：

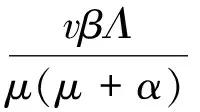
则V沿系统在时间t的导数为

(μ+ε+σ)(R-1)I(t)，

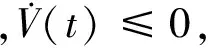
2 Hopf分支分析

考虑模型(1)的地方病平衡点：当R>1时，存在平衡点E*，

E*= (S*,I*,T*,R*)=

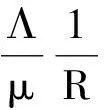
系统在E*处的雅克比矩阵如下：

显然，其对应的特征值有1个，为-μ<0, 其他3个特征根满足方程：

λ3+Eλ2+Fλ+G=(Hλ2+Jλ+K)e-λτ，

(5)

其中：

E=μR+2μ+α+ε+σ,

F=μR(2μ+α+ε+σ)+(ε+μ+σ)(μ+α),

G=μR(ε+μ+σ)(μ+α),

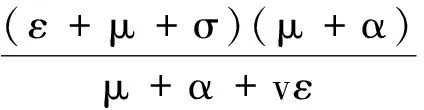
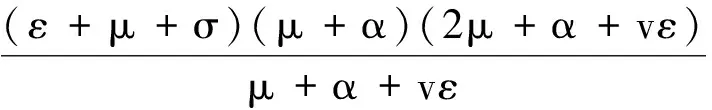
K=μ(ε+μ+σ)(μ+α)。

当时滞τ=0时，特征方程变为

λ3+a1λ2+a2λ+a3=0，

其中：

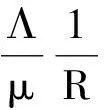
当R>1时，根据Routh-Hurwitz判据可知，E*局部渐近稳定。

当时滞τ>0时，不妨设λ=iω(ω>0)为方程(5)的根，则

-iω3-Eω2+Fiω+G=

(-Hω2+Jiω+K)e-iωτ，

分离实虚部有：

-ω3+Fω=Jωcosωτ-(K-Hω2)sinωτ,

-Eω2+G=(K-Hω2)cosωτ+Jωsinωτ,

平方后相加有：

(Fω-ω3)2+(G-Eω2)2=

J2ω2+(K-Hω2)2，

化简有：

ω6+h2ω4+h1ω2+h0=0,

令ψ=ω2,则ψ3+h2ψ2+h1ψ+h0=0,

其中：

h0=G2-K2,

h1=F2-2GE-J2+2KH,

h2=E2-2F-H2。

当R>max{1,R1}时，

h0=G2-K2=(G+K)(G-K)>0,

h1=μ2R2[(μ+α)2+(μ+ε+σ)2]-

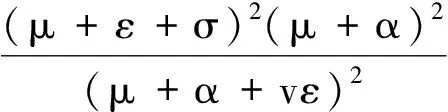
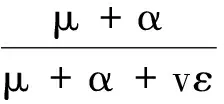
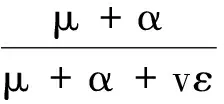
其中:

令

M(ψ)=ψ3+h2ψ2+h1ψ+h0。

根据笛卡尔符号法则可知：当h1>0时，M(ψ)=0没有正根，表示不存在λ=iω(ω>0)满足式(5)，故对任意τ平衡点E*均局部渐近稳定；当h1<0时，M(ψ)=0有2个或零个正根存在，假设有零个正根，则不存在λ=iω(ω>0)使得式(5)成立，则无论τ取何值，平衡点E*均局部渐近稳定；假设有2个正根，即存在λ=iω1,λ=iω2,ω1,ω2>0，使得式(5)成立，此时，

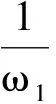
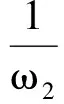
下面将τ作为分支参数进行分支分析，其中τ0=τ1或τ2，等式(5)的解为

λ(τ)=η(τ)+iω(τ),

η(τ0)=0,

ω(τ0)=ω0。

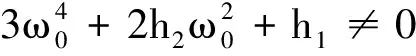
证明对式(5)两边对于τ求导，

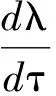
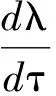
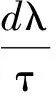
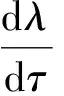
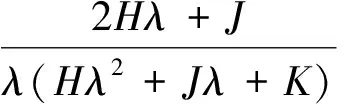
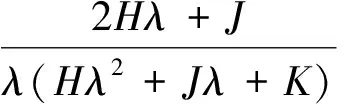
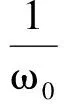
j=0,1,2…。

3 阈值分析

分析丙肝治疗者的恢复率、丙肝染病者的治疗率、有效接触率等参数对疾病传播动力学的影响，以便找到更好的方法来控制疾病的传播。首先对R关于参数α，β，ε分别求导，有：

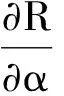
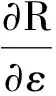
[v(μ+σ)-(μ+α)]，

因为治疗者的相对传染性较小(v<1)，治疗者的恢复率相对较高(α>σ)，则v(μ+σ)-(μ+α)<0,故基本再生数R会随着的增大而减小。

可以采取如下措施：

1)提高治疗者的恢复率α。研制新型抗病毒药物(如靶向给药)并使用，有效控制丙肝蔓延。

2)推广安全教育。推行安全注射；不共用剃须刀及牙具；加强对性乱史者和静脉吸毒者的安全教育和规劝；医务人员需遵守相关的预防规定，常戴手套、勤消毒等，减小有效传染率β，有效控制丙肝蔓延。

3)提高防御意识。通过网络、传媒等途径宣传丙肝的传播方式和预防措施，倡导居民进行定期体检。对携带丙肝病毒者进行及早诊断和治疗，提高染病者的治疗率ε，减少丙肝的流行和发生。

4 数值模拟

在R<1时，系统在无病平衡点E0处是全局渐近稳定的。参数如下：

Λ=5,μ=0.09,β=0.008,α=0.52,ε=0.3,v=0.85,σ=0.58。直接计算得:R=0.649 7。如图2所示，I，T趋向于0，故当R<1时，丙肝不再流行。

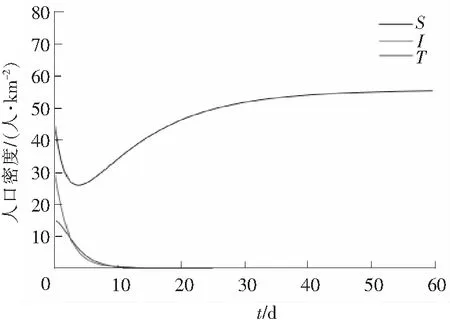
图2 R<1时，丙肝不再流行Fig.2 Hepatitis C virus is no longer popular when R<1

当R>1，选取如下参数：Λ=5,μ=0.08,β=0.06,α=0.5,ε=0.1,v1=0.5,σ=3,经计算得R=1.280 9,ω0≈0.350 6。

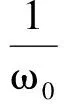
j=0,1,2,…,

可计算出τ0≈15.961 4。选取不同的τ，分别令τ=5，τ=50。如图3所示，S，I，T最后都趋于一条直线，故R>1且τ=5时E*趋于稳定。如图4所示，S，I，T最后都是波浪线，故R>1且τ=50时，E*是不稳定的。

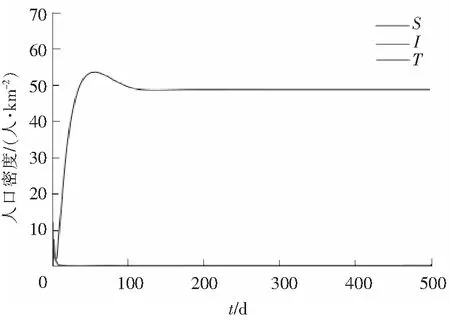
图3 R>1且τ=5时，E*趋于稳定Fig.3 E* tends to be stable when R>1 and τ=5

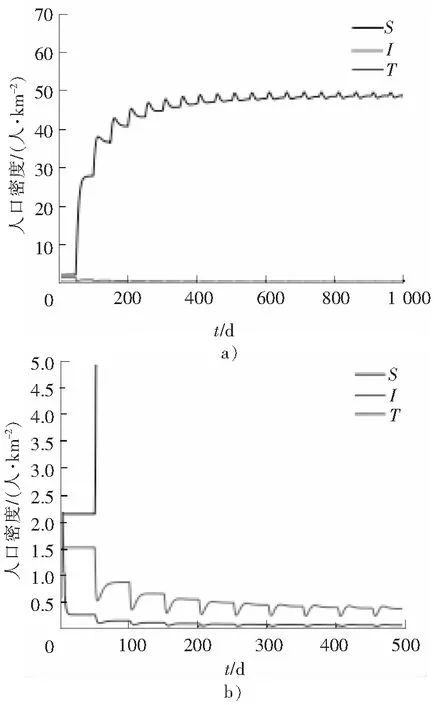
图4 R>1且τ=50，E*是不稳定的(b)是a)的局部放大)Fig.4 E* is unstable when R>1 and τ=50 (b) is a partial amplification of a))

5 结 论

本文利用常规的稳定性理论知识对模型进行深入分析与研究，考虑了无病平衡点和正平衡点的稳定性并且将时滞作为分支参数，求出产生Hopf分支的条件。研究表明，在传染病的研究范围里时滞有着很重要的作用，疾病的流行与否都与它的变化有直接的影响。到目前为止，世界上虽然没有预防丙肝的疫苗，但已经有了可以及时查出丙肝病毒的先进技术，有效地缩短了时滞，这在减少丙肝的流行和发生上具有重要作用。本研究为减少丙肝的流行提供了一种方法，不足的是只考虑了分支的存在性，后期可以在分支方向上进行具体研究，以获得更有价值的研究结果。

/

[1] MARTCHEVA M, CASTILLO-CHAVEZ C. Diseases with chronic stage in a population with varying size[J].Mathematical Biosciences, 2003, 182(1):1-25.

[2] KRETZSCHMAR M, WIESSING L. Modelling the Transmission of Hepatitis C in Injecting Drug Users[M].Lisbon: European Monitoring Centre for Drugs And Drug Addiction, 2004.

[3] PRASENJT D A S, MUKHERJEE D, SARKAR A K. Analysis of a disease transmission model of Hepatitis C[J]. Journal of Biological Systems, 2005, 13(4):331-339.

[4] ZEILER I, LANGLANDS T, MURRAY J M, et al. Optimal targeting of Hepatitis C Virus treatment among injecting drug users to those not enrolled in methadone maintenance programs[J]. Drug and Alcohol Dependence, 2010, 110(3):228-233.

[5] de VOS A S, KRETZSCHMAR M E. Benefits of Hepatitis C Virus treatment: A balance of preventingonward transmission and re-infection[J]. Current Opinion in Plant Biology, 2014, 258(3):11-18.

[6] ELBASHA E H. Model for Hepatitis C Virus transmissions.[J]. Mathematical Biosciences and Engineering Mbe, 2013, 10(10):1045-1065.

[7] NAZARI F, GUMEL A B, ELBASHA E H. Differential characteristics of primary infection and reinfection can cause backward bifurcation in HCV transmission dynamics[J]. Mathematical Biosciences, 2015,263:51-69.

[8] SUN C, HSIEH Y H. Global analysis of an SEIR model with varying population size and vaccination[J]. Applied Mathematical Modelling, 2010, 34(10): 2685-2697.

[9] MISRA A K, SHARMA A, SINGH V. Effect of awareness programs in controlling the prevalence of an epidemic with time delay[J]. Journal of Biological Systems, 2011, 19(2):389-402.

[10] XU R, WANG Z, ZHANG F. Global stability and Hopf bifurcations of an SEIR epidemiological model with logistic growth and time delay[J]. Applied Mathematics and Computation, 2015, 269(C): 332-342.

[11] 董亚丽,乔志琴.两种基因类型的丙肝传染病混合模型的动力学分析[J].河北工业科技,2017,34(1):1-6.

DONG Yali, QIAO Zhiqin. Dynamic analysis of mixture model about Hepatitis C Virus with two genetic types[J]. Hebei Journal of Industrial Science and Technology, 2017,34(1): 1-6.

[12] 秦文惠，张菊平.具有交叉感染的2种菌株对逼近模型分析[J]. 河北工业科技,2017,34(2):103-109.

QIN Wenhui,ZHANG Juping. Analysis of pair approximation model of two strains with the cross infection[J]. Hebei Journal of Industrial Science and Technology, 2017,34(2):103-109.

[13] 孔建云,刘茂省,王弯弯.一类带有时滞的SIR模型的稳定性及分支分析[J].河北工业科技,2017,34(3):167-171.

KONG Jianyun, LIU Maoxing, WANG Wanwan. Analysis of stability and bifurcation of a delayed SIR model[J]. Hebei Journal of Industrial Science and Technology,2017,34 (3): 167-171.

Analysis of Hepatitis C Virus model with time delay and treatment

ZHANG Liting, FENG Fei， DONG Yali， QIAO Zhiqin

(School of Science， North University of China, Taiyuan， Shanxi 030051， China)

In order to further study the mechanism of Hepatitis C Virus(HCV) transmission and effective methods for its treatment, aiming at the characteristics that the latent period of HCV is quite long and HCV is an infectious virus throughout the whole disease period, based on the existing model, the time delay is used to reflect the existence of the latent period of HCV. In order to study the effect of the time delay and the medical treatment on HCV, a model with the constant input and the time delay is established. The existence of equilibria is evaluated using the qualitative theory of ordinary differential equation, the global stability of the disease-free equilibrium is got by constructing the suitable Liapunov function, and the influence of the time delay on the system is also discussed. The analysis results show that if the time delay is greater than zero and the reproduction number is less than 1, the system is globally asymptotically stable at the disease-free equilibrium; the stable and unstable conditions of the endemic equilibrium are given, respectively, and the system can generate a Hopf bifurcation under the condition. Finally, the measures to control HCV are put forward by analyzing the threshold. The numerical simulation verifies the corresponding results. Therefore, it is significant to study the HCV model with the time delay and the medical treatment， and it can provide new ideas for reducing the prevalence of Hepatitis C.

theory of stability； Hepatitis C Virus； time delay； treatment； Hopf bifurcation

1008-1534(2017)06-0402-06

O175

A

10.7535/hbgykj.2017yx06003

2017-05-30;

2017-09-28；责任编辑：张 军

国家自然科学基金(11401541)；博士学科点专项科研基金(20111420120006)

张丽婷(1991—)，女，山西长治人，硕士研究生，主要从事生物数学方面的研究。

乔志琴副教授。E-mail:qiaozhiqin@nuc.edu.cn

张丽婷，冯 飞，董亚丽，等.具有时滞和治疗的丙肝模型分析[J].河北工业科技,2017,34(6):402-407.

ZHANG Liting,FENG Fei, DONG Yali ,et al.Analysis of Hepatitis C Virus model with time delay and treatment[J].Hebei Journal of Industrial Science and Technology,2017,34(6):402-407.