基于FxKalman算法的有源控制器设计与实现研究
梁清,王世闯,王晓林
基于FxKalman算法的有源控制器设计与实现研究
梁清,王世闯,王晓林
(杭州应用声学研究所,浙江杭州 310023)
近年来,对于有源噪声控制算法的性能越来越重视。与基于维纳滤波原理的最小均方滤波(Filtered-x Least Mean Square,FxLMS)、最小二乘滤波(Filtered-x Recursive Least Square,FxRLS)算法相比较,基于卡尔曼滤波的有源控制算法(Filtered-x Kalman,FxKalman)具有较快的收敛速度和良好的跟踪性能,且对带宽噪声有较好的降噪性能。设计、仿真运行了FxKalman算法的有源控制器,并针对单频、窄带和宽带信号,在实验室封闭空间对FxKalman算法、FxLMS算法和FxRLS算法进行有源控制器验证性实验比较,证实了FxKalman有源控制器具有上述优点。而如果初级噪声为单频信号且对算法收敛速度要求不高,FxLMS算法是最经济稳妥的选择。当需要控制带宽噪声或对算法收敛速度要求较高时,FxKalman算法则为最好的选择。
有源噪声控制;卡尔曼滤波;平均降噪量;性能代价比
0 引言
随着中国经济和工业化进程的不断发展,噪声污染已经成为一个不容忽视的环境问题。有源噪声控制是根据声波的相消性干涉原理,初级声源发出期望信号,次级声源通过生成一个与初级源幅度相等、相位相反的辐射声波,对期望信号进行抵消,从而达到降低噪声的目的,其消声原理如图1所示。1981年,J. C. Burgress[1]首次将自适应滤波理论应用于有源噪声控制系统,提出了著名的最小均方滤波(Filtered-x Least Mean Square,FxLMS)算法。Kuo和Morgan[2]在其专著中介绍了基于RLS的最小二乘滤波(Filtered-x Recursive Least Square,FxRLS)算法。从80年代起研究所、清华大学、哈尔滨工业大学、西北工业大学及南京大学也开展了有源噪声控制的研究[3-4],但还没有利用卡尔曼滤波算法进行有源控制的实例。由于卡尔曼滤波算法中存在大量矩阵相乘以及求逆的过程,因此该算法的运算量较高。本文主要研究利用卡尔曼滤波算法实现封闭空间有源噪声控制器的设计,并通过相关实验将该算法与FxLMS算法、FxRLS算法进行比较,完成了基于卡尔曼滤波(Filtered-x Kalman,FxKalman)算法的有源控制器设计与实现研究。

图1 有源噪声控制中声波抵消示意图
1 卡尔曼滤波算法
在控制领域,科学家早已经发现了一种随着系统状态变化而对步长进行相应调节的算法——卡尔曼滤波算法[5-6],该算法的核心内容是进行系统的状态估计。在最小均方误差准则以及最小干扰原理的共同作用下,卡尔曼滤波算法约束并优化问题。也就是说,自适应卡尔曼滤波器权系数的迭代是按照最小方式进行变动的。虽然最小均方算法LMS (Least Mean Square,LMS)和最小二乘RLS (Recursive Least Squares,RLS)算法是基于维纳滤波原理的,但它们仍与卡尔曼滤波算法存在着不小的关联:利用最小二乘法求目标函数的最小范数值是LMS算法的核心思想,以这一思想为基础也建立了LMS算法和RLS算法之间重要的数学联系;此外RLS算法可以看作卡尔曼滤波算法的特例。
卡尔曼滤波器是由其发明者匈牙利数学家卡尔曼提出的。该算法是建立在线性最小方差估计原理上,与之前所研究的基于维纳滤波器的FxLMS算法和FxRLS算法有所不同,卡尔曼滤波算法引入了系统的状态空间模型以及状态变量等概念,因此有着更为广阔的应用环境,特别是在非平稳环境下,卡尔曼滤波算法的性能要远优于基于维纳滤波的算法。状态空间可以理解为两方面:其一是指状态空间矩阵与输入的关系,其二是状态矩阵对输出结果所产生的影响。其算法思想是在得到系统的输入以及输出所需的相关估计值之后,对参数进行反复的估计与修正,从而获得最优的结果。其特点是[6]:可进行算法递推、能够适用于非平稳过程,适用于连续型算法和离散型算法。
基本的卡尔曼滤波算法已很成熟。这里给出卡尔曼滤波的时间更新方程以及状态更新方程。
(1) 时间更新方程如下:


(2) 状态更新方程如下:

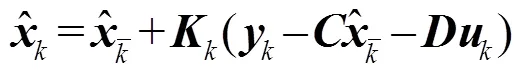

下面将基本的卡尔曼滤波算法应用于有源噪声控制系统中,推导出FxKalman。
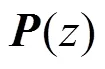

图2 有源控制系统框图




图3 有源控制系统等价框图
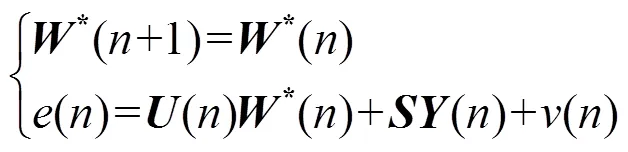
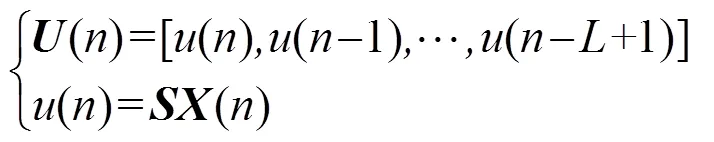

通过上述推导得到了在有源噪声控制系统中的卡尔曼滤波状态方程。表1总结了FxKalman算法的流程。

表1 FxKalman算法流程
2 实验系统简介
通过编写基于Simulink的自适应有源噪声算法程序和次级通路离线建模程序,通过使用实时系统完成了自适应控制器的实现,并在封闭空间内完成了实验,将FxLMS、FxRLS与FxKalman算法进行对比。
实验系统利用个人计算机作为上位机,利用Matlab中的Simulink工具箱搭建了三种算法模块,并利用Xpc Target将搭建好的模块编译成C语言,将代码传递给下位机。下位机有多通道的AD和DA端口,通过AD端口采集误差传感器所得的电压信号输入到自适应算法模块中。自适应算法模块根据误差信号和参考信号,利用算法自动调整滤波器权系数,通过DA端口传递给次级声源使其工作。详见3.3节中自适应控制器的实现原理。
具体仪器名称以及其用途如表2所示。

表2 实验仪器及功能
3 自适应控制器的实现
3.1 搭建三种算法模块
如上文所述,为了实现自适应控制器,第一步要在Simulink中搭建三种算法模块并进行仿真以验证搭建模块的正确性,通过查找相关资料可以发现,Simulink自带的工具箱中只包含了最为基础的LMS、RLS等自适应模块,并没有FxLMS、FxRLS和FxKalman算法模块,而Simulink自身提供的算法模块与在输入输出参数以及滤波器权系数的迭代方法和本文所研究的三种算法有较大的差异,导致在仿真和实际应用时不能使用已有模块来实现。因此,本文尝试采用S函数构建三种算法模块。
S函数按照所支持功能分类包括Level 1和Level 2。如,编写简单数学算法用来仿真时,只需要M语言编写的Level 1 M S函数;所编写的算法需要传递多个输入输出端口且每个端口数据都是多维(矩阵)时,需要使用Level 2 M S函数。综上所述,对有源控制算法模块有以下几点考虑:
(1) 有源控制算法为典型的多输入多输出算法,因此选择Level-2 S函数。
(2) Level-2 S函数局域Dwork向量,可以将Dwork向量理解为Simulink中的缓存区,可以对初始向量赋初值设定维度。在算法执行循环调用时,可以利用这一向量存储算法中的输入输出向量以及矩阵元素等,该缓存区的优点为能避免数据在循环调用时被覆盖。
(3) 在编写完相应的算法模块后,需要编写该算法的目标语言编译器(Target Language Compiler,TLC)文档,TLC文档也可称为目标语言编译文档,利用该文档可以将搭建的模块编译生成目标C代码,在接下来的工作中将目标代码下载到micro-box以供后续使用。
Level-2 S函数使得使用用户能够用Matlab语言来编写支持多输入/多输出端口的自定义模块,且其提供了一系列应用程序编程接口(Application Programming Interface,API)设置模块属性和定义各个子方法,其中Setup和Outputs两个子方法是必不可少的,通过对有源算法的分析,在建立三种模块时用到了以下几种API:
(1) Setup函数体
实现对模块的初始化,构建三种算法模块过程中,Setup 函数主要功能如下:
① 对模块的输入参数个数以及输出参数个数进行了规定:本文中有3个输入,分别为参考信号、滤波信号和误差信号,2个输出信号:控制信号和自适应滤波器权系数;
② 对输入参数的维度、数据类型、复杂性以及数据的采样频率进行设定,本模块中维度为1,数据类型为double类型,复杂度为实数,采样频率默认为继承方式;
③ 对模块中的参数进行设置,在本文所使用的三个模块中分别设置了3个不同的参数,它们为步长、遗忘因子和干扰信号波动。
(2) CheckPrms函数体
该模块是用来检验所输入的参数是否合法,因为参数都有一定的取值范围,当参数超出给定的取值范围时,系统就会报错。
(3) DoPostPropSetup函数体
① 对于FxLMS算法建立3个Dwork向量,分别为“”变量(参考信号)、“”变量(滤波信号)、“”(自适应滤波器系数),设置变量的初始属性,用于数据更新。
② 对于FxRLS和Kalman滤波算法建立4个Dwork向量,分别为“”变量(参考信号迭代)、“”变量(滤波信号迭代)、“”(权值迭代)、“”(协方差矩阵迭代),设置变量的初始属性,用于数据更新。
(4) Start函数体
将Dwork内的多个初始向量赋值为0,将协方差矩阵赋值为单位矩阵。
(5) Outputs函数体
根据三种算法的原理设计相应的程序,算法框图如图4所示,通过计算得到控制信号和相应的自适应滤波器权系数,并将相应结果传递至输出端口。
3.2 对算法模块的验证
为了验证所编写模块的正确性,现将这三个模块应用在有源噪声控制算例中进行仿真。初级信号是频率为100 Hz、幅值为1的单频噪声,初级通路和次级通路均使用FIR滤波器进行模拟,自适应滤波器的阶数为32,可以通过点击模块设置模块的参数,例如FxLMS算法中的步长、FxRLS算法中的遗忘因子等。
初级通路的传递函数为[7]
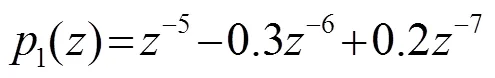
次级通路的传递函数为

图5为利用FxLMS算法模块搭建的仿真模型,相应的FxRLS和FxKalman算法的仿真模型也与之相似,只需将其中的FxLMS模块换成相应的FxRLS模块和FxKalman模块即可。
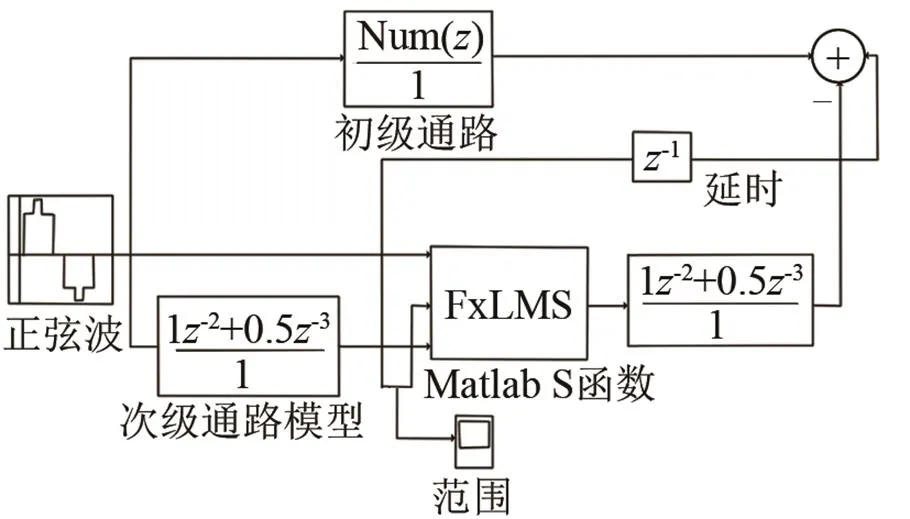
图5 利用Simulink搭建的算法模型
图6(a)~6(c)是三种编写模块的仿真结果,通过图6可知,对于单频信号三种算法的降噪性能相似,而在收敛速度方面,FxKalman算法略优于FxLMS算法和FxRLS算法。后面又对窄带及宽带噪声的性能进行观察,验证三种算法模块的正确性,为后面自适应控制器的实现奠定了基础。

(a)FxLMS算法
(b)FxRLS算法
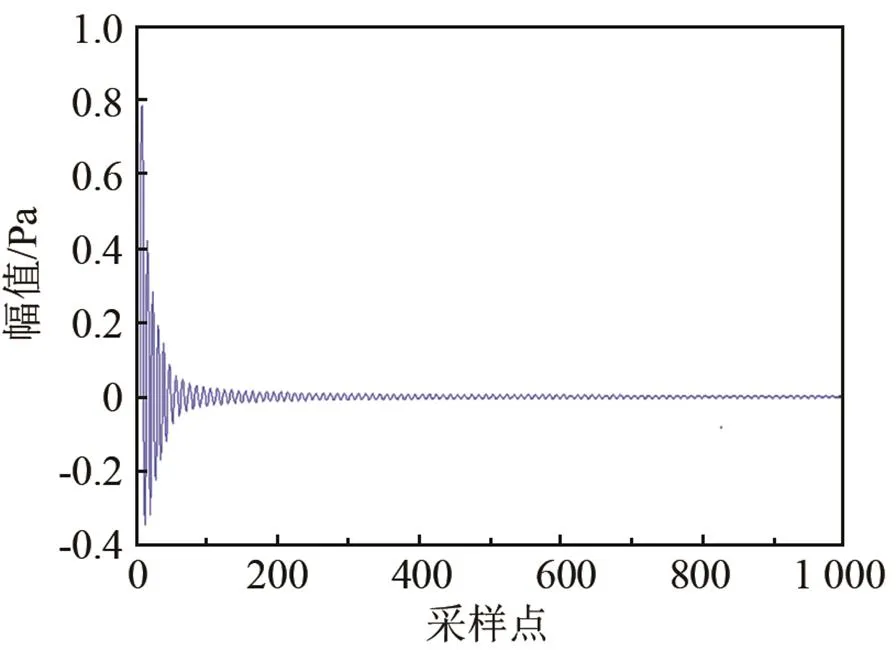
(c)FxKalman算法
3.3 自适应控制器的实现
将这三种算法模块及Micro-box实时操作系统,完成自适应控制器的设计与实现。控制器实现的原理如图7所示。
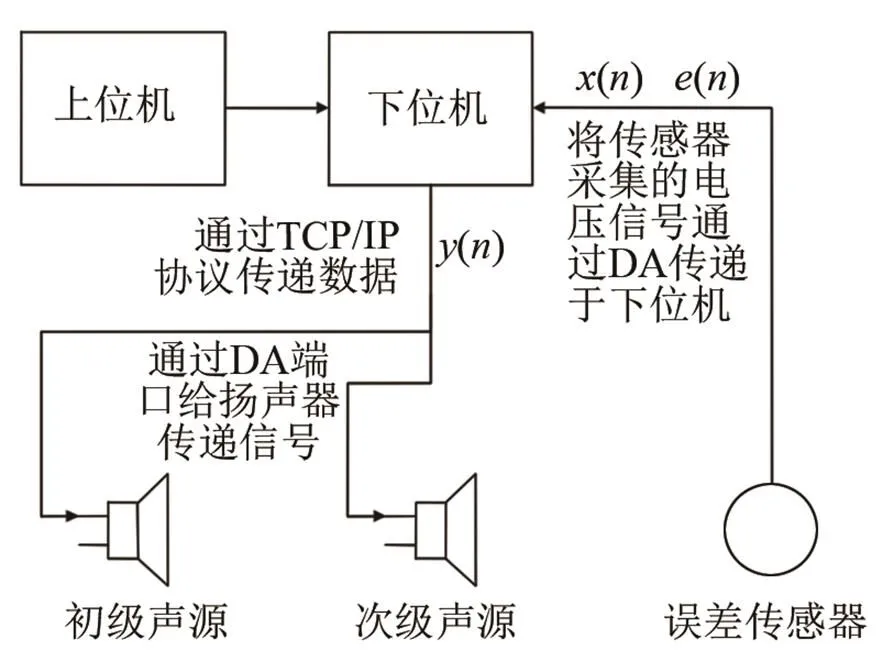
图7 自适应控制器的实现原理
4 现场实验
实验系统如图8所示,由1个初级声源、1个次级声源和1个误差传感器构成。将三者布放于同一水平高度,初级声源距离误差传感器距离为2 m,次级声源距离误差传感器为1 m,初级声源距离次级声源为1 m,自适应滤波器长度为32,次级通路(次级声源到误差传感器之间的通路)长度为200。实验分别对100 Hz单频噪声,中心频率为200 Hz、带宽为50 Hz的窄带噪声以及中心频率为350 Hz、带宽为500 Hz的宽带噪声进行研究,检验算法的实际性能是否和仿真结果相一致。

图8 封闭空间内的实验系统
图9为对单频信号进行有源噪声控制过程中下位机采集到的实时数据,通过观察可以看出,图片由四幅子图构成。左上为控制器所得参考输入信号,左下为滤波-信号,右上为误差传感器采集的误差信号,右下为次级声源的驱动信号即控制器输出的次级信号。由于下位机中无法对数据进行定量的分析,将下位机采集到的数据传递给上位机并在Matlab中完成数据分析。

图9 下位机实验中采得的实时数据
(1) 单频信号
同仿真结果类似,由图10(a)~10(c)可以看出,对于单频信号,在收敛速度方面FxKalman算法有着最好的性能,而FxRLS算法和FxLMS算法的收敛速度大致相同。对于单频信号的降噪性能,由图11(图中①表示FxLMS算法,②表示FxKalman算法,③表示FxRLS算法)可以看出,三种算法性能接近,平均降噪量都在17 dB左右。
(2) 窄带信号
对于窄带信号,由图12(a)~12(c)可以看出,FxKalman算法需要800次迭代可达到收敛,FxRLS算法需要2 000次迭代才可收敛,而FxLMS算法则需要3 500次迭代。由图13(图中①表示FxLMS算法,②表示FxKalman算法,③表示FxRLS算法)可以看出,在降噪量方面,FxKalman算法有着较为明显的优势,平均降噪量可以达到14.1 dB,FxRLS算法的平均降噪量为11.4 dB,而FxLMS算法的降噪量只有11.2 dB。
(a) FxLMS算法
(b) FxRLS算法

(c) FxKalman算法
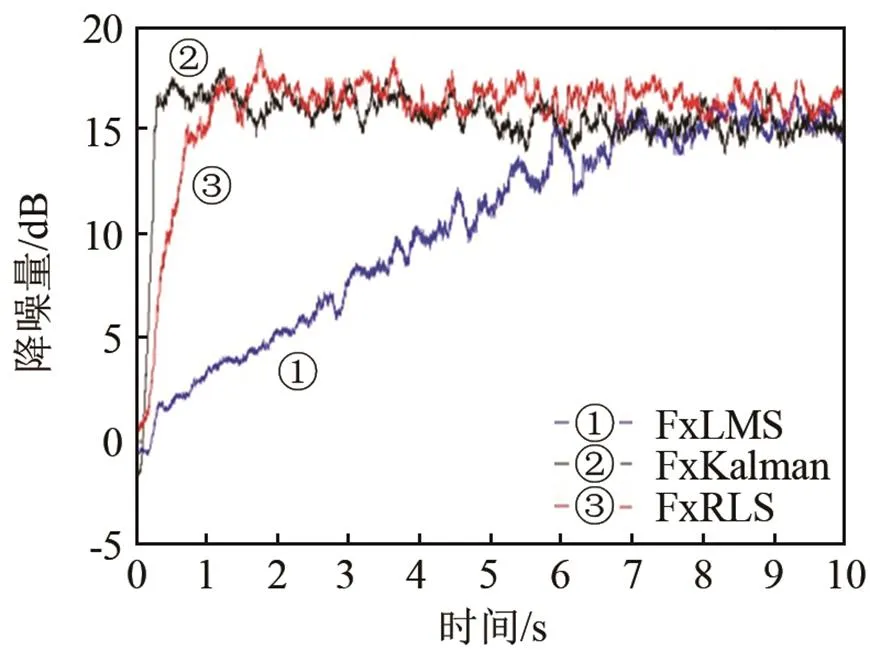
图11 三种算法降噪量比较(单频信号)
(3) 宽带信号
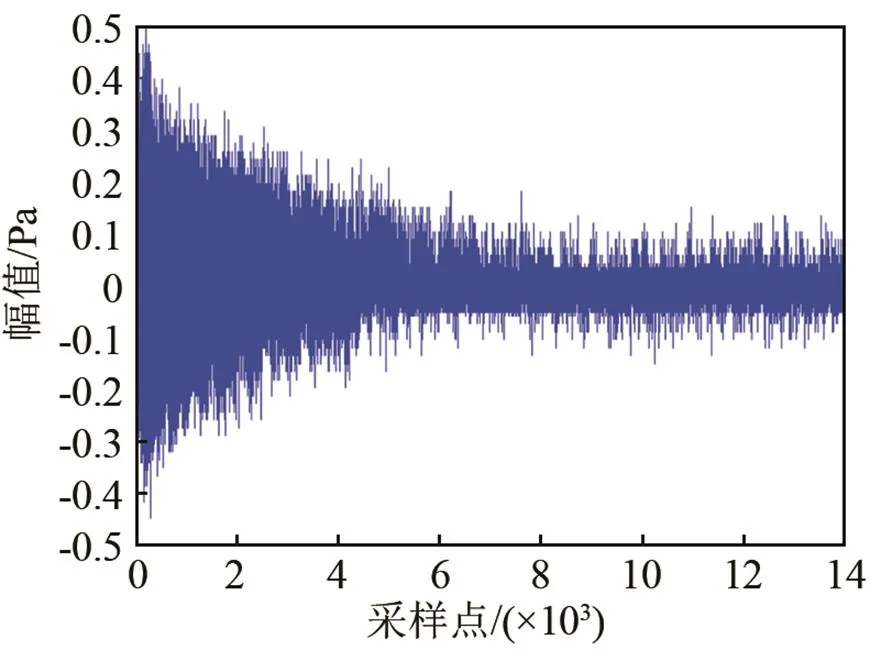
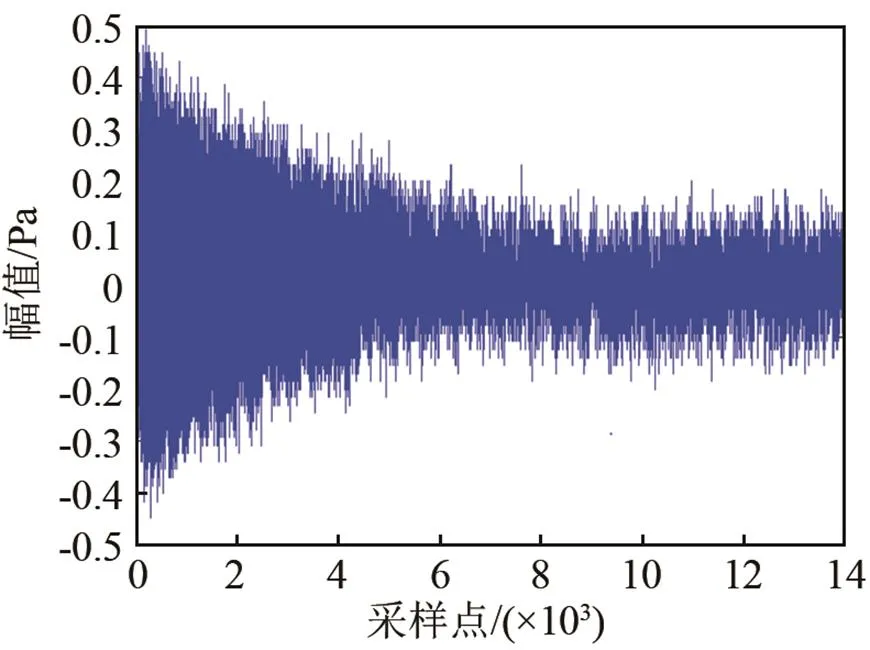
对于宽带信号来说,由图14(a)~14(c)可以看出,FxKalman算法需要500次迭代可达到收敛,FxRLS算法需要1 500次迭代即可收敛,而FxLMS 算法则需要3 000次迭代。由图15(图中①表示FxLMS,②表示FxKalman算法,③表示FxRLS算法)可以看出,在降噪量方面,FxKalman算法有着较为明显的优势,平均降噪量可以达到15.3 dB,FxRLS算法的平均降噪量为12.4 dB,而FxLMS算法的降噪量只有10.7 dB。
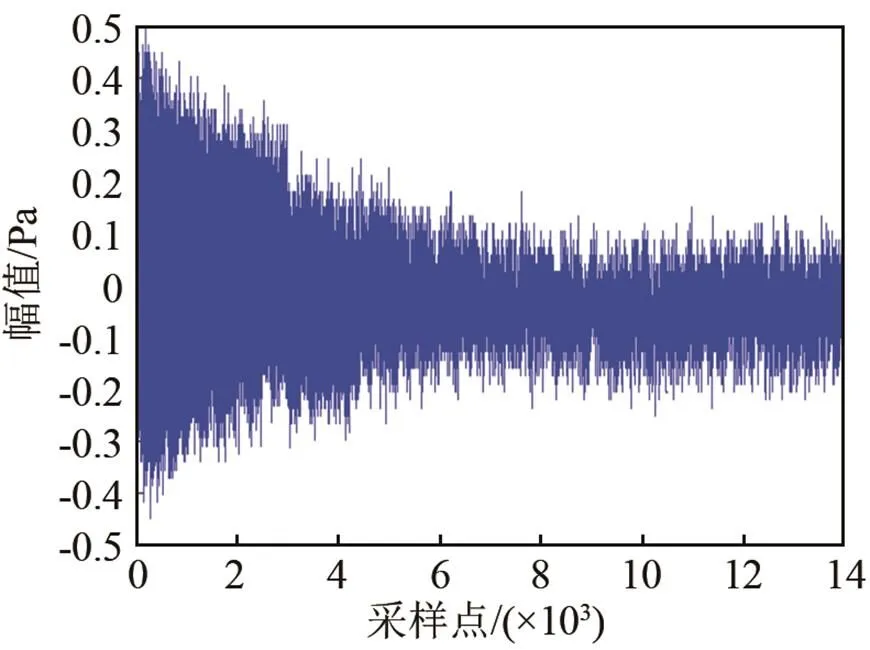
(a) FxLMS算法
(b) FxRLS算法

(c) FxKalman算法

图13 三种算法降噪量比较(窄带信号)
(a)FxLMS算法
(b)FxRLS算法

(c) FxKalman算法
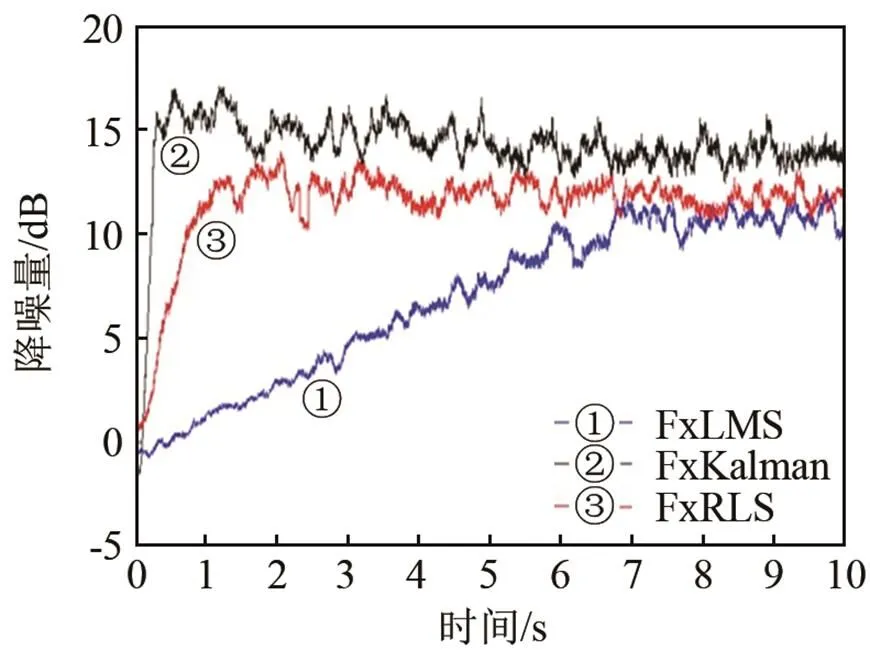
图15 三种算法降噪量比较(宽带信号)
通过实验可得到以下几个结论:
(1) FxKalman算法具有较快的收敛速度
和仿真所得结果类似,无论控制信号是单频信号,还是窄带噪声或宽带噪声,FxKalman算法相较于FxLMS算法和FxRLS算法,在收敛速度方面都有较为明显的提升。
(2) FxKalman算法降噪性能突出
对于单频信号来说,三种算法的降噪性能相似。但是因为FxLMS算法对于带宽噪声性能并不突出,所以对于窄带和宽带噪声来说,FxLMS算法的降噪量都要低于FxRLS算法和FxKalman算法。FxRLS算法虽然降噪性能相较于FxLMS有所提升,但还是略逊于FxKalman算法,具体的比较如表3所示。
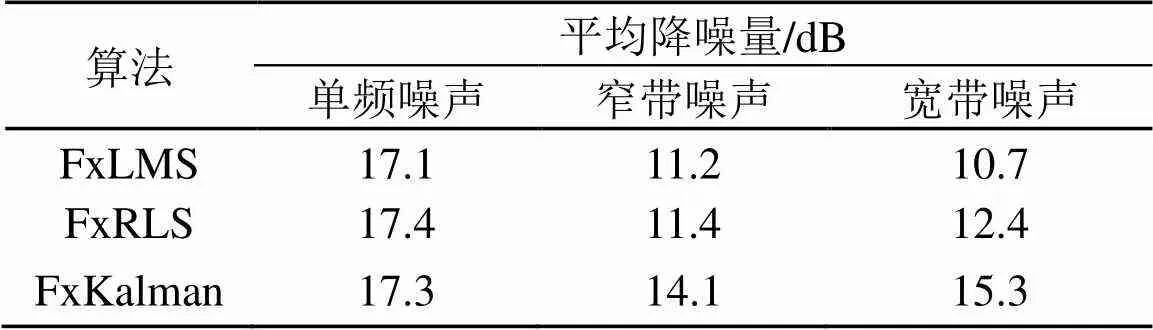
表3 三个算法的平均降噪量(次级通路长度为200)
定义算法的性能代价比为稳态误差或平均误差与运算量的比值,表4中加粗的数字表示该类型噪声的最大性能代价比。由表4可以看出,在三种情况下,FxLMS算法的性能代价比仍然最高,这也是FxLMS算法在收敛速度较慢的情况下,仍是现在较为主流的自适应算法的原因。FxRLS算法和卡尔曼滤波算法两者的性能代价比很接近,而FxKalman算法在三种情况下平均降噪量都接近或者优于FxRLS算法。所以在硬件条件满足的前提下,FxKalman算法拥有较快的收敛速度、并且降噪性能最为优秀,是最为合适的选择。

表4 三个算法的性能代价比(次级通路长度为200)
注:加粗的数字表示该类型噪声的最大性能代价比。
5 结论
本文利用搭建的算法模块和Micro-box实时仿真系统,完成了一种新的自适应有源控制器FxKalman的设计和实现。并在实验室环境下进了实验研究,验证了FxKalman算法的降噪性能和收敛速度都要优于FxLMS算法和FxRLS算法,在宽带噪声情况下其降噪性能约提高了3~5 dB。在实际应用中,如果初级噪声为单频信号且对算法收敛速度要求不高,运算量不是很大,FxLMS算法是最经济稳妥的选择。当需要控制带宽噪声或对算法收敛速度要求较高时,FxKalman算法则为更好的选择。由于硬件条件的限制、本文中只实现了单通道的有源噪声控制,如果硬件条件许可,后续工作可以考虑进行多通道的有源噪声控制。
[1] Burgess J C. Active adaptive sound control in a duct, a computer simulation[J]. J. Acoust. Soc. Am., 1981, 70(3): 715-726.
[2] Kuo S M, Morgan D R. Active noise control: A tutorial review[J]. Proceedings of the IEEE, 1999, 87(6): 943-973.
[3] 盛美萍, 王敏庆, 孙进才. 噪声与振动控制技术基础[M]. 北京: 科学出版社, 2001. SHENG Meiping, WANG Minqing, SUN Jincai. Noise and vibration control technology[M]. Beijing: Science Press, 2001.
[4] 宫赤坤, 张从敏. 基于卡尔曼滤波的有源噪声自适应逆控制[J]. 噪声与振动控制, 2008, 28(3): 96-99. GONG Chikun, ZHANG Congmin. Active noise based on kalman filter adaptive inverse control[J]. Journal of Noise and Vibration Control, 2008, 28(3): 96-99.
[5] Elliott S J. Signal processing for active control[M]. London: Academic Press, 2001.
[6] BAMBANG R T. EKF learning in recurrent neural networks for nonlinear active noise control[J]. Applied Soft Computing, 2008, 8(4): 1498-1504.
[7] PETERSEN C D, FRAANJE R, CAZZOLATO B S, et al. A Kalman filter approach to virtual sensing for active noise control[J]. Mechanical Systems and Signal Processing, 2008, 22(2): 490-508.
[8] 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2001. CHENG Peiqing. Digital signal processing course[M]. Beijing: Tsinghua University Press, 2001.
Design and implementation of FxKalmanbased active noise controller
LIANG Qing, WANG Shi-chuang, WANG Xiao-lin
(Hangzhou Applied Acoustics Research Institute, Hangzhou 310012,Zhejiang,China)
In recent years, the researchers pay more attentions on the performance of active noise control (ANC) algorithms. Compared with the FxLMS and FxRLS algorithms, the Kalman filtering algorithm enjoys a faster convergence speed, a better tracking performance and a better noise reduction capability for broadband noise. In this paper, the FxKalman active controller is designed and simulated, and for single-frequency, narrowband and broadband signals, the active noise control performances of FxKalman algorithm, FxLMS algorithm and FxRLS algorithm are compared in the enclosed-space of the laboratory. Finally, the above-mentioned advantages of FxKalman active controller are proved. However, in the case that the primary noise is a single-frequency signal and the demand for convergence rate of the algorithm is not high, the FxLMS algorithm is the most economical and secure.The FxKalman algorithm is the best choice for broadband noise control or for high convergence speed demand.
active noise control; Kalman filtering;average noise reduction value; performance cost ratio
TB535
A
1000-3630(2017)-05-0491-08
10.16300/j.cnki.1000-3630.2017.05.016
2016-11-29;
2017-02-22
梁清(1991-), 女, 浙江诸暨人, 硕士研究生, 研究方向为噪声控制, 信号检测。
梁清, E-mail: snowy91@163.com

