T(0,1)模态导波在弯管上传播的仿真与实验

李阳，邹云，张双楠，蔡桂喜



T(0,1)模态导波在弯管上传播的仿真与实验

李阳1，邹云1，张双楠2，蔡桂喜2

(1. 郑州大学机械工程学院，河南郑州 450001；2. 中国科学院金属研究所，辽宁沈阳 110016)

由于弯管的几何形状复杂，超声导波在弯管中的传播特性比在直管中复杂。弯管超声导波检测中，衡量其检测有效性的一个重要参数是透过率。通过有限元模拟研究了激励频率、弯曲半径、弯管角度对T(0,1)模态导波透过率的影响。发现：不同激励频率的导波在弯管上有不同的透过率，并且激励频率高的导波由于脉冲宽度小，更易产生新的波前；在不同的弯曲半径和弯曲角度的弯管中，最小透过率的T(0,1)模态导波的频率也各不一样；随弯管角度的变化，信号的透过率呈规律性变化。通过实验验证了不同激励频率下，T(0,1)模态导波透过率和激励频率的关系。在实际检测有弯管段的管道时，需采用多频率检测。

透过率；弯管；T(0,1)模态；传播特性

0 引言

自Gazis[1-2]推导出空心圆管中的导波频散方程以来，超声导波引起了科研人员的极大关注。导波在直管上的传播机制，以及一些特征体对导波的反射已有了深入研究。近年来，无损检测仪器公司纷纷推出了各自的导波设备，使得超声导波检测技术进入了一个崭新的阶段。但是，一些导波检测应用难题仍未得到很好的解决，需要更完善的理论指导。如：由于超声导波在弯管上的传播特性相对直管变得复杂，而导致超声导波在弯管和过弯管后的检测灵敏度较低。为解决这个问题，科研人员对此进行了大量的研究。国外，Takahiro Hayashi[3]等在准柱坐标系上建立了弯管有限元模型，利用半分析有限元方法模拟了导波在弯头的传播过程，减少了计算时间。A Demma[4]等将弯管视为圆环的一部分，利用有限元方法计算了频率和速度的关系，画出了弯管的频散曲线，发现导波经过弯管后的透过率和管子的形状、激励导波的频率等因素有关。R M Sanderson[5]等将经过弯管后的信号看成是进入弯管前直管上的信号与弯管结构响应函数的卷积，利用有限元方法分析了不同弯管的响应函数。Hideo Nishino[6]等利用宽频激光超声激励导波，研究了纵向模态L(0,1)导波在弯管中转换为弯曲模态F(1,1)的现象，弯管的弯曲角度越大，模态转换得越严重。国内，周邵萍[7]等人研究了纵向模态L(0,2)超声导波在90°弯管中的传播特性，并分析了L(0,2)模态超声导波对弯管内缺陷的检测敏感性，发现弯头外侧的缺陷更易被检测到；并建议采用多个频率进行实际检测。邓菲[8]等人采用激励宽频导波的研究方法，可快速选择出管状结构检测的最优导波模态和激励频率，这可为弯管检测中最优激励频率的选取提供参考。王悦民[9]等人利用磁致伸缩导波检测技术，发现弯管中的导波能量的衰减与激励频率存在密切联系。

通过以上研究可知，导波在弯管中的传播过程比较复杂，具有特殊的传播特性，如：模态转变、能量集中、透过率变化等。其中，弯管上导波的透过率[4]定义为：特定模态导波经过弯管后横截面上该模态合成信号的峰-峰值除以过弯管前信号的峰-峰值。通过导波的透过率，可反映出导波对弯管后缺陷的检测灵敏度。因此，弯管超声导波检测中，衡量其检测有效性的一个重要参数是透过率。由于T(0,1)模态导波无频散，且T(0,1)模态导波的质点振动只包含周向分量而不含径向和轴向分量，所以在检测有液体浸没的管道或运输液体的管道时，T(0,1)模态导波衰减小，传播距离远，因此T(0,1)模态是应用最为广泛的导波检测模态之一[10]。为利用T(0,1)模态导波检测有弯管段的管道，需要清楚地了解影响导波在弯管上透过率的因素，并观察导波在弯管中的传播现象。

本文通过一系列有限元模拟和实验，研究T(0,1)模态导波在弯管上透过率的变化规律，并找出影响导波透过率的因素，以此来指导超声导波在工程检测中激励频率的选择。首先，利用有限元方法模拟激励频率、弯曲半径和弯曲角度对T(0,1)模态导波经过弯管后透过率的影响。然后，通过实验验证在不同的激励频率下，导波透过率与激励频率的关系。

1 有限元模拟

1.1 有限元模型

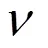
图1 弯管模型示意图。其中，A-A和B-B为接收位置，R为弯曲半径，θ为弯曲角度。横截面上任意质点的三个位移分量：Da为轴向位移，Dc为周向位移，Dr为径向位移。

Fig.1 Geometry of the FE model, where the position A-A and B-B are the receiving points, R represents bend radius and θ represents bend angle. Three displacement components of each node on the cross section: Da represents axial displacement, Dc represents circumferential displacement and Dr represents radial displacement

管上每点的振动可分解为三个分量：周向位移、径向位移和轴向位移，其中周向位移和径向位移在质点所在横截面的面内，周向位移垂直于半径方向，径向位移与半径方向重合，轴向位移方向垂直于横截面与管的轴向平行。在图1管子的激励端所有节点上，加载相同的周向位移载荷信号，信号为加汉宁窗的5周期正弦函数信号，以激励出特定频率的T(0,1)模态导波。在两个接收位置A-A和B-B的管壁上，均匀分布12个点接收周向位移导波信号，如图1所示。规定：点1对应的角度为180°，点4对应的角度为90°，点7对应的角度为0°，点10对应的角度为-90°。

1.2 激励频率与透过率的关系

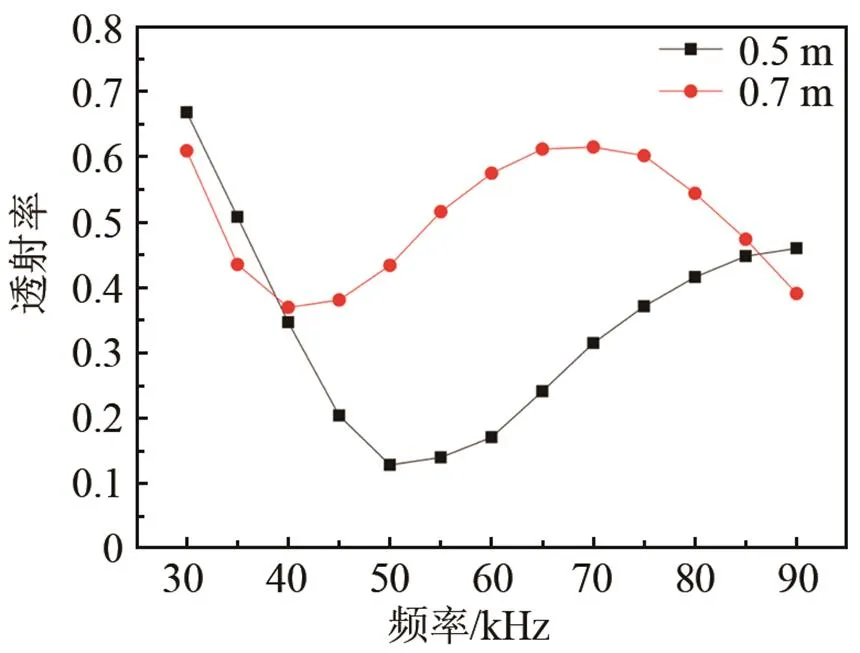
图2 在弯曲角度90°、弯曲半径分别为0.5 m和0.7 m的弯管上，T(0,1)模态导波经过弯管的透过率与激励频率的关系

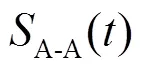
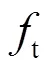
(a) 弯曲半径为0.7 m

(b) 弯曲半径为0.5 m

图3 不同激励频率下，T(0,1)导波的频域信号

Fig.3 Frequency spectrums of receiving mode T(0,1) after propagating through bends with (a) 0.7 m and (b) 0.5 m at different excitation frequencies

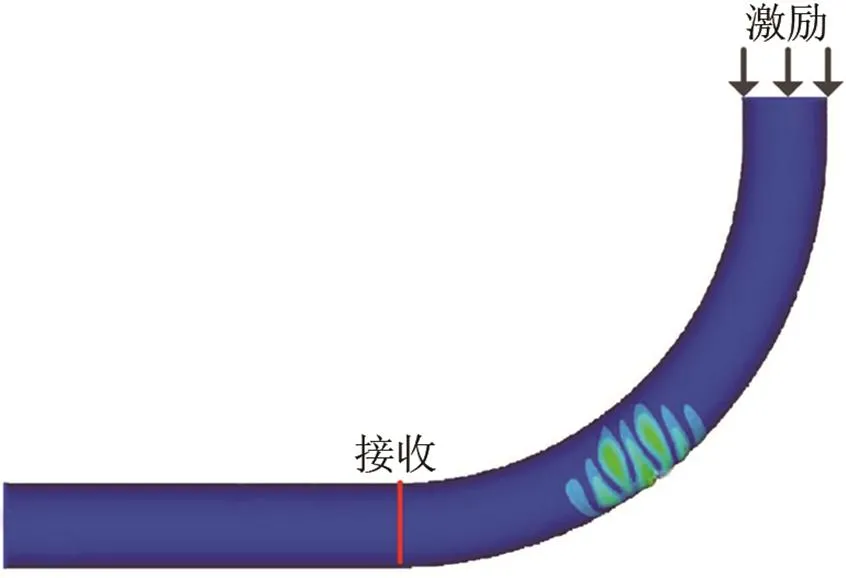
根据Brath[13]等人和Qi[14]等人的研究，导波在弯管中传播一定距离后会产生新的波前，这是由于弯管的外侧传播距离长、内侧传播距离短，内侧波前向外侧扩展，传播一定距离后形成新的波前。将激励频率提高到150 kHz，在弯曲半径为0.5 m、弯管角度为90°的弯管上激励T(0,1)模态导波。对比激励频率为50 kHz和150 kHz两个模型，导波在弯管上传播的形态和所提取的T(0,1)模态导波信号，如图4所示。

从图4(a)和4(b)可以看出：激励频率为150 kHz相较于50 kHz，弯管中有新波前产生，新波前从弯管内侧向外侧扩展。将接收位置A-A处的12个点所收到的时域波形以周向分布形式画出，如图4(c)和4(d)所示。其中，横轴代表时间，纵轴代表角度位置，图中颜色代表位移幅度。对比图4(c)和4(d) 可知：激励频率为50 kHz时比150 kHz时的T(0,1)导波脉冲宽度大，各点信号严重不均衡。50 kHz时，由于低频导波有更大的波长，所以相同的周期数下脉冲更宽，那么新产生的波前和原波前未能分离开，导致两者相互叠加形成干涉，引起透过率的降低；而150 kHz时，由于导波脉冲较窄，新形成的波前和原波阵面清晰可辨，所以干涉效果较弱。因此，150 kHz时的透过率会大于50 kHz时的透过率，如图4(e)和4(f)所示。在图4(a)～4(d)中，两种频率下的导波能量分布和集中程度也不一致，但能量都在弯管外侧集中较强。

(a) 激励频率为50 kHz，波动位移分布图

(b) 激励频率为150 kHz，波动位移分布图

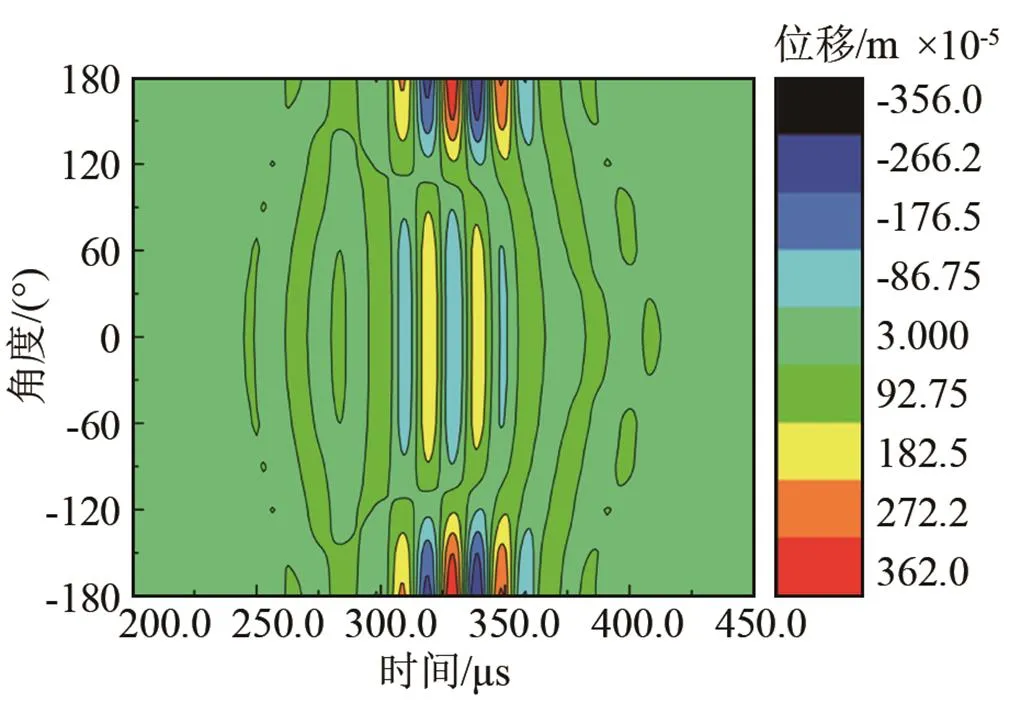
(c) 激励频率为50 kHz，接收位置A-A上12个点的信号周向分布图

(d) 激励频率为150 kHz，接收位置A-A上12个点的信号周向分布图

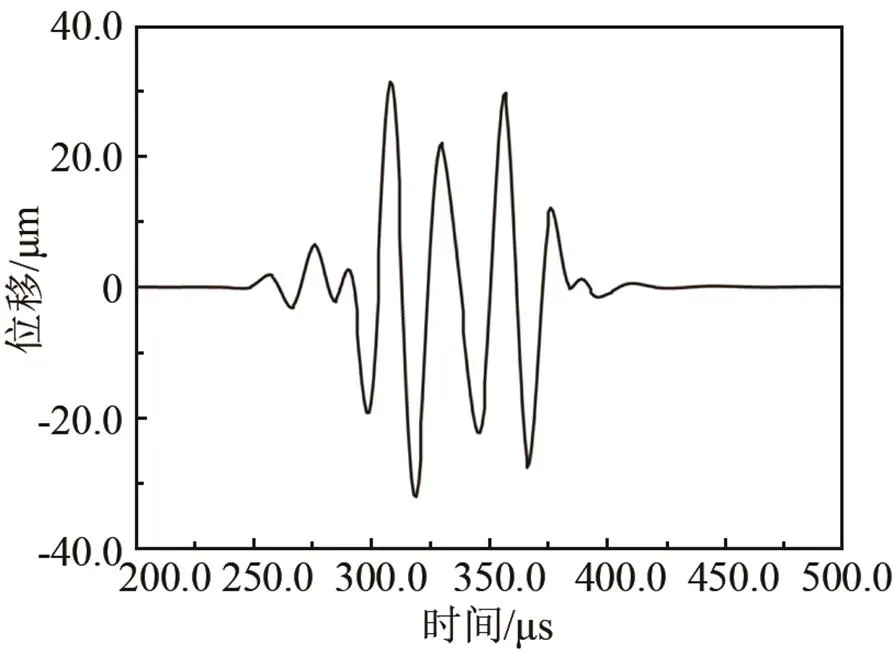
(e) 激励频率为50 kHz，T(0,1)导波信号

(f) 激励频率为150 kHz，T(0,1)导波信号

图4 激励频率分别为50 kHz和150 kHz时：(a)与(b)是某时刻导波在弯管上的波动位移分布图；(c)与(d)是过弯管接收位置A-A上12个点的信号周向分布图；(e)与(f)是由12个接收信号相加所提取的T(0,1)导波信号

Fig.4 When the excitation frequencies are respectively 50 kHz and 150 kHz, the displacement contours of the bend are shown in (a) and (b); the displacements at 12 evenly circumferential points are shown in (c) and (d); and the signals of T(0,1) mode after adding the 12 received signals are shown in (e) and (f)

1.3 弯曲半径和透过率的关系

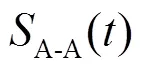
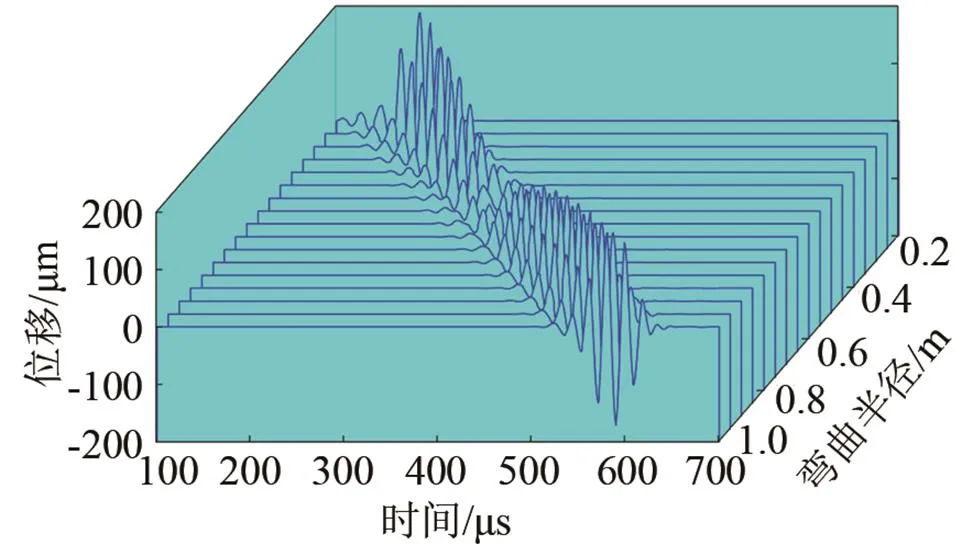
(a) 时域信号

(b) 透过率随弯曲半径的变化曲线

图5 在弯曲角度为90°时，不同弯曲半径弯管上的接收信号及透过率

Fig.5 (a)- the received signals of T(0,1) mode after propagating across the bends of 90° bend angle with different bend radii and (b)- the transmission coefficients vs. the bend radius

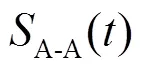
图6 经过不同弯曲半径的弯管后，T(0,1)模态导波的频域信号

从图7可知：激励频率50 kHz的T(0,1)模态导波分别经过弯曲半径0.5 m和1.0 m的弯管后，接收端的12个信号不仅在幅度上而且在相位上也存在差别。当12个信号相加提取T(0,1)模态导波时，由于导波经过弯曲半径0.5 m的弯管后的12个信号相位相差大(如图7(a))，所以形成相减干涉，导致透过率降低；而导波经过弯曲半径1.0 m的弯管后的12个信号相位相近(如图7(c))，所以透过率降低较小。

1.4 弯管角度和透过率的关系

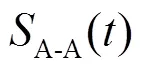
(a) 弯曲半径为0.5 m时，接收端7点接收的时域信号

(b) 弯曲半径为0.5 m时，导波T(0,1)信号

(c) 弯曲半径为1.0 m时，接收端7点接收的时域信号

(d) 弯曲半径为1.0 m时，导波T(0,1)信号

图7 弯管弯曲半径为0.5 m和1.0 m时，A-A接收端7点接收的时域信号分别为(a)、(c)；A-A接收端12个信号相加后提取的T(0,1)导波信号分别为(b)、(d)

Fig.7 When the bend radius are respectively 0.5 m and 1.0 m, the seven signals received at the seven points of the A-A monitoring end are shown in (a) and (c) and the signal of T(0,1) mode from adding 12 signals received respectively at the 12 points of the A-A monitoring end are shown in (b) and (d)

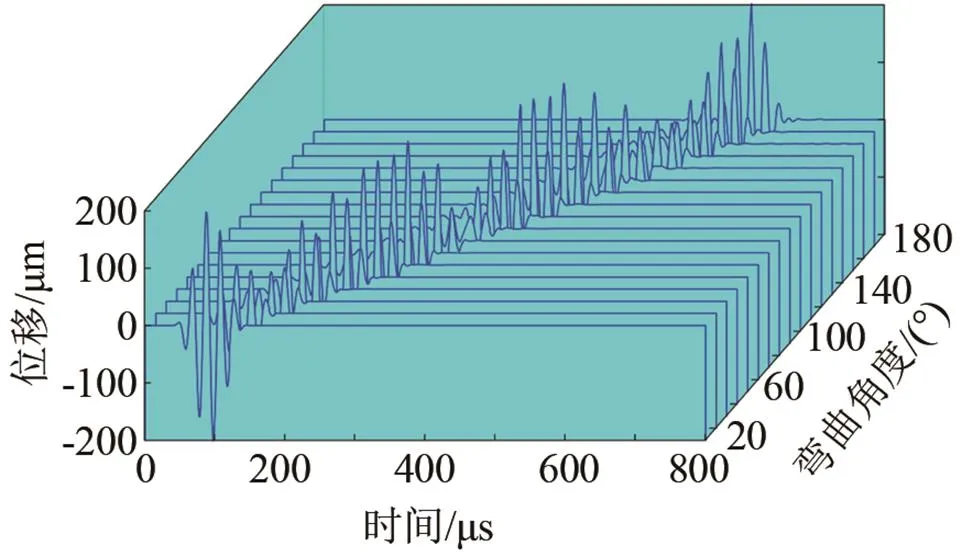
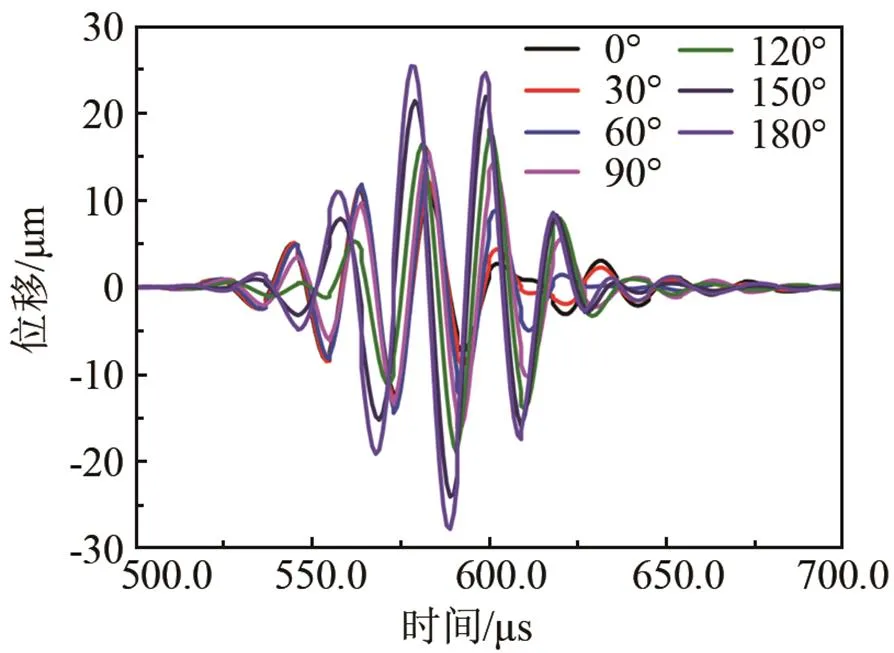
(a) T(0,1)模态态导波的时域信号

(b) 透过率随弯曲角度的变化曲线

图8 在弯曲半径0.5 m的不同弯曲角度的弯管上接收的信号及透过率

Fig.8 (a)- the received signals of T(0,1) mode after propagating across the bends of 0.5 m bend radius with different bend angles and (b)- the transmission coefficient vs. the bend angle

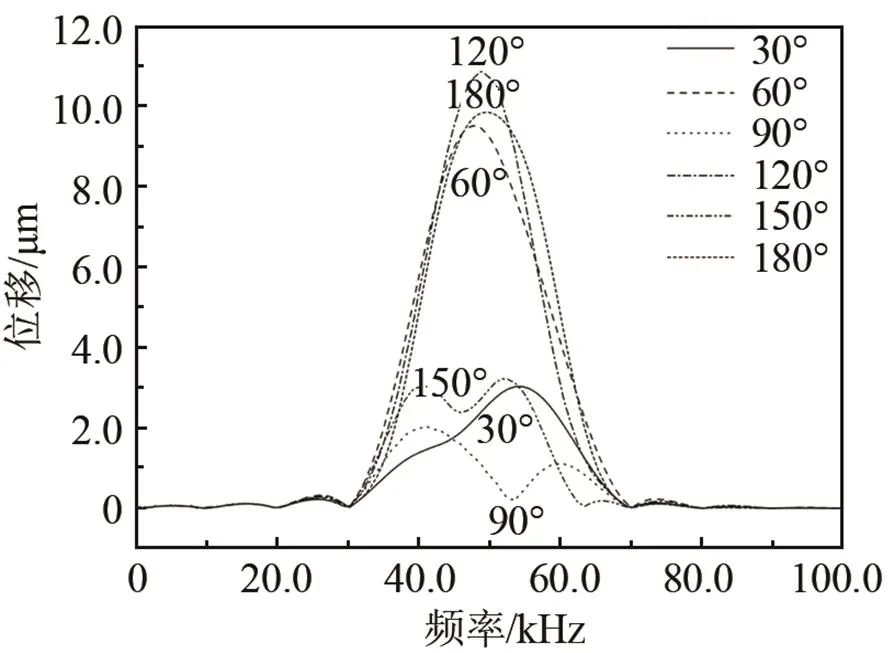
图9 经过不同角度的弯管，T(0,1)模态导波的频谱曲线

由图9可知：在弯曲角度为30°、90°和150°的弯管上都发生了相减干涉，并且90°和150°弯管上的频谱曲线都出现了波谷，且最小值出现在不同的频率上。

2 实验

2.1 实验材料及方法

实验用弯管的规格：外径108 mm，壁厚8 mm。弯管角度90°，弯曲半径0.7 m，管子的材料为45#钢。采用自制导波检测仪和探头环，探头环由周向均匀分布的12个横向切变模的压电探头组成，并可通过机械装置装卡在管子外壁上。探头使管外壁周向振动，激励T(0,1)模态导波。导波激励信号为加汉宁窗的5周期正弦函数信号。在弯管的两端分别布置探头环A和探头环B，如图10所示。探头环B激励T(0,1)导波，导波经过弯管后被探头环A接收，其接收信号的峰峰值记为I；然后，将探头环B装卡在距离探头环A相同距离1.1 m(弯管段的长度)的直管段上，探头环A接收信号的峰峰值记为II。那么，T(0,1)导波经过弯管后的透过率=I/II。

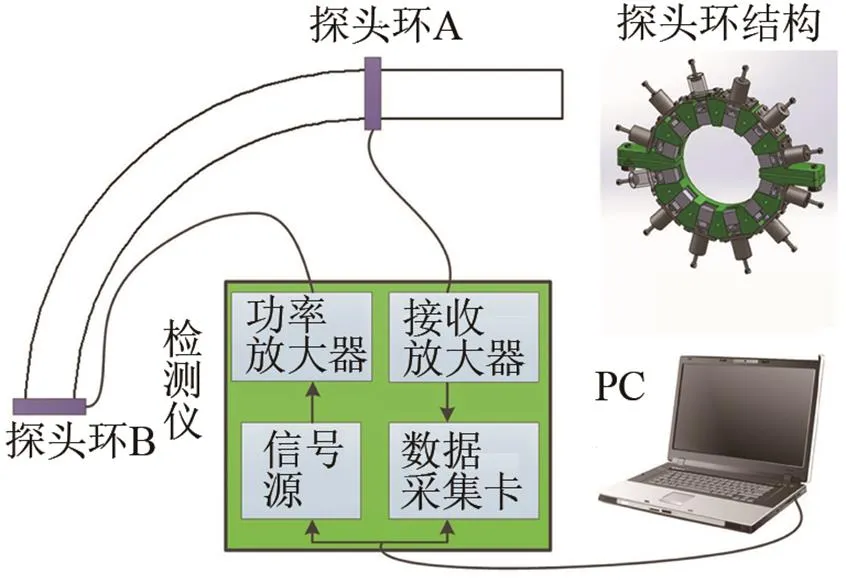
图10 检测装置示意图

2.2 实验结果

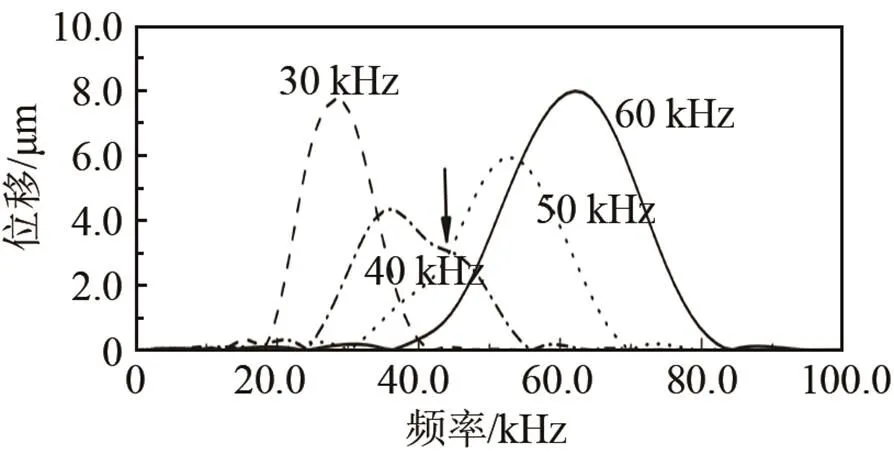
改变探头的激励频率从25 kHz到85 kHz，以5 kHz的间隔变化。其中，激励频率为30 kHz的T(0,1)模态导波信号如图11(a)所示，从时域信号中计算得到T(0,1)模态导波的群速度为3 323 m/s，与理论计算得到的群速度相差不大，由此可说明管中的导波为T(0,1)模态。对导波信号进行傅里叶变换，得到如图11(b)中的信号频谱图。从图11(b)中可以看出，导波信号的中心频率大致为30 kHz，说明探头的性能良好。得到不同激励频率下透过率和激励频率的关系，如图12所示。

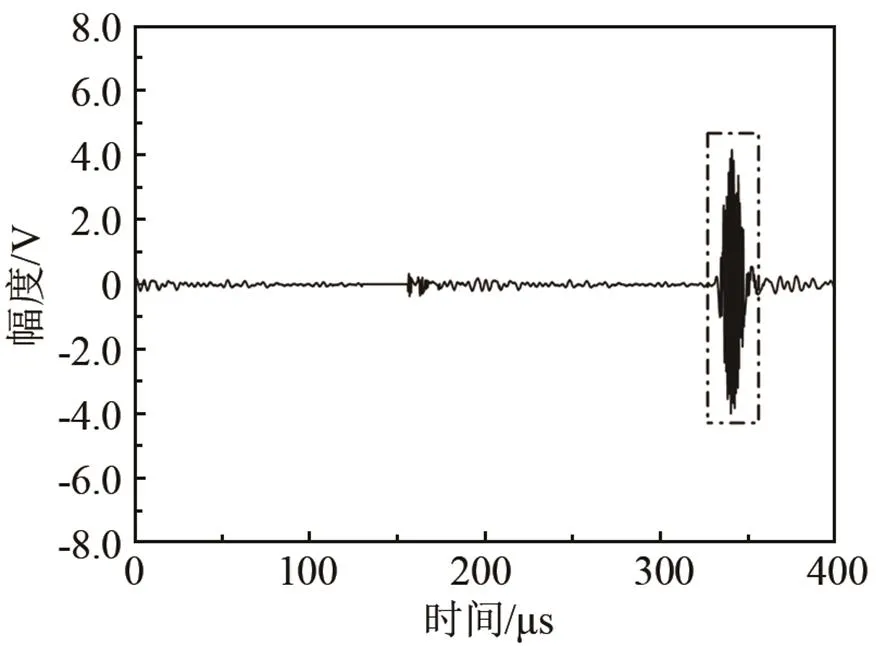
(a) 时域信号

(b) 频域信号

图11 探头环A接收到的探头环B激励的30 kHz的T(0,1)模态信号

Fig.11 (a)- the signal of T(0,1) mode activated by ring B and (b)- the signal received by ring A

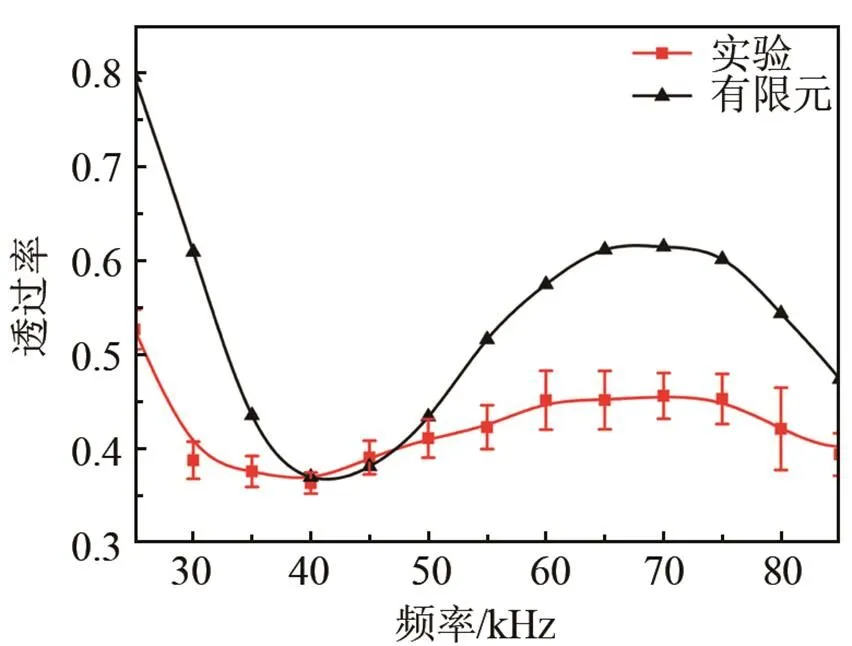
图12 不同激励频率下的透过率

从图12中可知：实验结果和有限元模拟结果有一定的误差，但是在整体的变化趋势上是一致的。误差来源的可能原因：其一，由于探头环需要两次机械装卡，无法保证装卡的一致性；其二，探头环上的12个探头无法保证其性能完全均匀一致。因此，在提取T(0,1)模态导波时，实验结果不能得到有限元模拟的理想结果。在实际检测中，频率选择不当就会造成透过率很小，如实验中40 kHz时的情况。

3 结论

T(0,1)模态导波在经过弯管时，由于探头环安装在管子的某个截面上，导波在弯管上传播到达探头环的各个探头的时间就不同，使探头环的各通道接收的信号产生相位差异，不同的激励频率产生不同的相位差，从而形成了不同程度的干涉，造成弯管透过率的变化。

由于弯管参数不同，导致各个通道接收信号的相位差变化。因此，T(0,1)模态导波在不同弯曲半径、弯曲角度的弯管上传播时，形成不同程度的干涉，导致透过率变化。

激励频率为50 kHz的T(0,1)模态导波，在弯曲角度为90°的弯管上，其透过率随弯管角度呈周期性变化。

为了避免相减干涉的发生，提高信号的透过率，应采用多个频率来检测有弯管段的管道。

[1] Gazis D C. 3-Dimensional investigation of the propagation of waves in hollow circular cylinder. 1. analytical foundation[J]. J. Acoust. Soc. Am., 1959, 31(5): 568-573.

[2] Gazis D C. 3-Dimensional investigation of the propagation of waves in hollow circular cylinders. 2. numerical results[J]. J. Acoust. Soc. Am., 1959, 31(5): 573-578.

[3] Hayashi T, Kawashima K, Sun Z Q, et al. Guided wave propagation mechanics across a pipe elbow[J]. J. Pressure Vessel Technol., 2005, 127(3): 322-327.

[4] Demma A, Cawley P, Lowe M, et al. The effect of bends on the propagation of guided waves in pipes[J]. J. Pressure Vessel Technol., 2005, 127(3): 328-335.

[5] Sanderson R M, Hutchins D A, Billson D R, et al. The investigation of guided wave propagation around a pipe bend using an analytical modeling approach[J]. J. Acoust. Soc. Am., 2013, 133(3): 1404-1414.

[6] Nishino H, Yoshida K, Cho H, et al. Propagation phenomena of wideband guided waves in a bended pipe[J]. Ultrasonics, 2006, 44: 1139-1143.

[7] 周绍萍, 张蒲根, 吕文超, 等. 基于导波的弯管裂纹缺陷的检测[J]. 机械工程学报, 2015, 51(6): 58-65. ZHOU Shaoping, ZHANG Pugen, LÜ Wenchao, et al. Detection of cracks in elbow pipes using guided waves[J]. Journal Of Mechanical Engineering, 2015, 51(6): 58-65.

[8] 邓菲, 陈洪磊, 张僖. 基于宽频激励的管型结构导波检测[J]. 机械工程学报, 2014, 50(18): 23-28. DENG Fei, CHEN Honglei, ZHANG Xi. Pipe structure detection based on broadband guided wave excitation[J]. Journal of Mechanical Engineering, 2014, 50(18): 23-28.

[9] 王悦民, 宗侣, 朱龙翔, 等. 多弯头管道磁致伸缩导波无损检测技术[J]. 海军工程大学学报, 2015, 27(2): 42-45. WANG Yuemin, ZONG Lü, ZHU Longxiang, et al. Guided wave non-destructive testing technology of multi-elbow pipe based on magnetostrictive effect[J]. Journal of Naval University of Engineering, 2015, 27(2): 42-45.

[10] Alleyne D N, Pavlakovic B, Lowe M J S, et al. Rapid long-range inspection of chemical plant pipework using guided waves[J]. Insight, 2001, 43(2): 93-98.

[11] 赵继辰, 吴斌, 何存富. 螺旋波纹管导波检测技术的数值仿真和试验研究[J]. 机械工程学报, 2012, 48(24): 8-13. ZHAO Jichen, WU Bin, HE Cunfu. Numerical simulation and experimental research on helical bellows by using guided wave technology[J]. Journal of Mechanical Engineering, 2012, 48(24): 8-13.

[12] 程载斌, 王志华, 张立军, 等. 管道超声纵向导波裂纹检测数值模拟[J]. 应用力学学报, 2004, 21(4): 76-80. CHENG Zaibin, WANG Zhihua, ZHANG Lijun, et al. Ma hongwei. numerical simulation of crack detection in pipes using ultrasonic longitudinal guided wave[J]. Chinese Journal of Applied Mechanics, 2004, 21(4): 76-80.

[13] Brath A J, Simonetti F, Nagy P B, et al. Guided wave radiation from a point source in the proximity of a pipe bend[J]. 40th Annual Review of Progress in Quantitative Nondestructive Evaluation: Incorporating the 10th International Conference on Barkhausen Noise and Micromagnetic Testing, 2014, 33a& 33b(1581): 316- 323.

[14] QI Minxin, ZHOU Shaoping, NI Jing, et al. Investigation on ultrasonic guided waves propagation in elbow pipe[J]. International Journal of Pressure Vessels and Piping, 2016, 139-140:250-255.

Numerical and experimental research on T(0,1) guided waves propagating in bended pipes

LI Yang1, ZOU Yun1, ZHANG Shuang-nan2, CAI Gui-xi2

(1. School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001,He’nan, China;2. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016,Liaoning, China)

Propagation of guided waves in bended pipes is more complicated than that in straight pipes because of the complex geometry of bends. The transmission coefficient is an important factor used to evaluate the accuracy of the test. In this study, the finite-element method (FEM) is used to investigate the influences of the angle of bends, the radius of bends and the excitation frequencies on the transmission coefficients of T(0,1) guided waves. Our results show that the transmission coefficients varied with the excitation frequencies of guided waves when propagating through a bend. Given that the frequency of guided wave is high enough, new wave fronts are more easily produced after the guided wave propagating through a bend. It is also found that when guided waves propagating through a bend with the minimal transmission coefficient, their frequencies are correlated with the angle and the radius of the bend. The transmission coefficients oscillate periodically with increasing angle of the bend. The correlation between transmission coefficients and frequencies of the guided waves is verified by experimental data. In conclusion, it is suggested that guided waves propagating at various frequencies should be used to test bended pipes.

transmission coefficients; bended pipes; T(0,1) mode; propagation characteristic

TB559

A

1000-3630(2017)-05-0442-08

10.16300/j.cnki.1000-3630.2017.05.008

2016-09-13;

2016-12-30

河南省教育厅高等学校重点科研项目(18A460032)

李阳(1988－), 男, 河南焦作人, 博士, 讲师, 研究方向为超声导波的工程化应用。

李阳, E-mail: yangli@zzu.edu.cn