一种基于波数积分方法的线源声场计算方法
于晓林,骆文于,杨雪峰,张仁和
一种基于波数积分方法的线源声场计算方法
于晓林1,2,骆文于1,杨雪峰2,3,张仁和1
(1. 中国科学院声学研究所声场声信息国家重点实验室,北京 100190;2. 中国科学院大学,北京 100049; 3. 中国科学院声学研究所东海研究站,上海 201815)
提出了在Pekeris波导条件下,一种基于波数积分方法的线源声场中的稳定数值计算方法。通过对深度格林函数中上行波与下行波的归一化,得到稳定的系数矩阵,从而求得格林函数的解析解。对深度格林函数进行模式展开,验证了该方法得到的深度格林函数解析解的准确性。结合仿真实例,将该方法得到的波数积分模型与传统简正波模型KRAKENC的结果进行比较,结果显示,当某号简正波的波数与海底波数接近时,KRAKENC计算不出该号简正波,会导致KARKENC的计算结果不准确,而波数积分方法可以很好地解决该问题。因此,提出的方法可以作为Pekeris波导中线源激发声场的标准模型。
线源问题;波数积分;稳定性解法
0 引言
Pekeris波导作为一个经典声传播问题环境模型,是由Pekeris在1948年发表的文章中首次较完整地提出并给出了海上试验结果[1]。布列霍夫斯基赫在其专著中对该问题进行了详细推演,得到完备的近似解析式[1]。国内的声学专著将该模型作为一般分层波导模型的特例给予相应的研究[3-4]。
现有的主要声场建模理论方法包括简正波方法[5-6]、波数积分方法[7]、抛物方程法[8]、有限元方法[9]等。其中,简正波方法是研究比较多而且应用比较广的一种方法。早期被广泛引用的一篇文献出自于Pekeris[1],他提出了简单的两层海洋模型的理论,Graves R[10]等人在一篇概述文章中提到了简正波方法研究方面取得的进展。简正波方法的基本原理是把积分拓展到复平面,应用柯西原理通过计算围道内的留数来计算原积分,一般在处理时忽略了分支线积分,所以简正波理论在较近距离上存在较大误差,一定距离之外精度较高。随着工程实践的发展,对近距离声场理论的需求日益紧迫,而在某些特殊情况下,如低频浅海声学环境中,由于传播模式比较少,传统简正波理论对近距离的声场的计算结果不再准确。
波数积分方法是对水平分层介质的积分变换法的数值实现方法,声场解的形式是深度分离波动方程解的谱积分。水平分层介质的波数积分原理是Pekeris首先引入到水声学中的[1],他使用了简单的两层和三层环境模型来处理分层平面波导中的声传播。波数积分方法与简正波方法的主要区别在于积分处理方法上的不同。简正波方法是使用复围线积分将积分表达式简化成留数之和,而波数积分方法采用的是直接数值求积分的方法,因而其对声场的计算更为准确。
国内对波数积分方法的研究相对比较少。姚万军在文献[11]中讨论了波数积分的实现方法,并强调了数值实现过程中的重点。国外也有一些文献把波数积分方法扩展到与距离无关的海洋环境的研究[12-13],但都有一定的局限性。
文献[14]以及文献[15]中给出了在Pekeris波导条件下,点源问题的波数积分的计算方法。理论推导可以发现,由于这两篇文献都没有对积分核函数做合理的归一化,因而会造成线性方程组的数值溢出,为了避免该问题,需要在求解过程中对积分核函数进行合理的归一化,从而保持方程解数值的稳定性。
注意的是,在现有的文献中,所有基于波数积分方法的数值模型的理论以及仿真都是关于点源的,还没有基于波数积分方法的关于线源的详细推导以及仿真,故本文只给出相应的线源解。
1 理论
在海洋声学中,亥姆霍兹方程是许多重要数值方法的理论基础,这些数值方法包括波数积分方法、简正波方法、抛物方程方法等。
1.1 亥姆霍兹方程的处理
在处理亥姆霍兹方程之前,需要选择合适的坐标系。一般来讲,边界条件是个复杂因素,坐标系的选择主要由边界条件决定。在对与距离无关的问题使用分离变量法的时候,必须选用其中有一个坐标轴与水平界面垂直的坐标系。已有文献中的理论推导以及分析主要集中在点源问题的处理上,本文将点源与线源问题进行了比较,并将重点放在对线源问题的分析以及仿真中。
对于与距离无关的问题,亥姆霍兹方程取以下形式[14]:
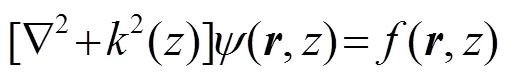
1.1.1 点源问题
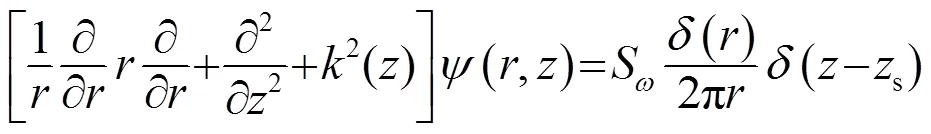

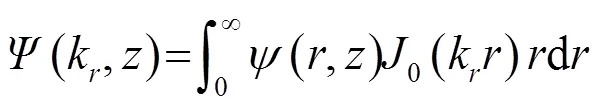
得到点源的深度分离波动方程:
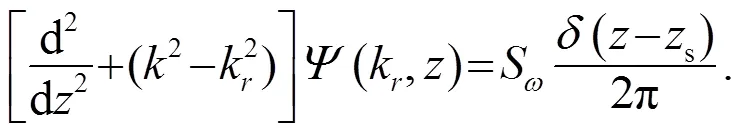
1.1.2 线源问题

利用傅里叶变换对,


得到线源的深度分离波动方程:


1.2 格林函数的求解
从前面的分析可知,点源问题与线源问题格林函数的求解方法是一样的,因而点源问题的格林函数的结果也可以应用到线源之中。
在文献[14]与文献[15]这两篇文献中,分别给出了两种不同的计算深度格林函数的线性方程组。可发现:两篇文献给出的线性方程组,由于没有做归一化,容易导致数值溢出问题,因此如果用这两种方法处理线源问题,同样会存在数值溢出问题。
下面分析两篇文献中深度格林函数数值溢出的原因,然后通过合理的归一化,从而求得数值稳定的格林函数。
在文献[14]中,海水中的上行波与下行波都以海面为参考点,方程为

由于海底为半无限空间,只有下行波,并且以海底界面为参考点,方程为
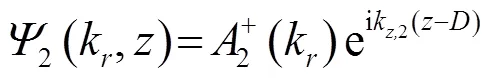

图1 Pekeris波导问题的示意图
由于海面处声压为0,

且海水—海底界面处压力连续和法向质点振速连续,


可求得系统方程为
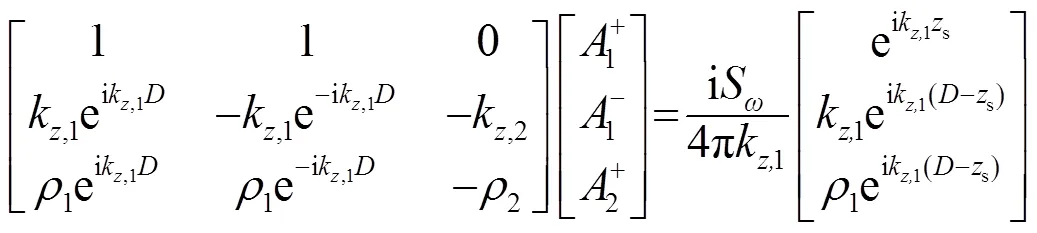
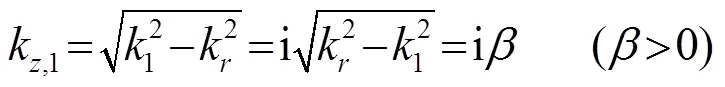
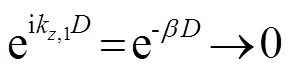

因此,方程(15)在实际仿真中容易造成数值的溢出。
在文献[15]中给出了另外一种计算深度格林函数的系统方程组。水中下行波以海底为参考点,上行波以海面为参考点,方程为
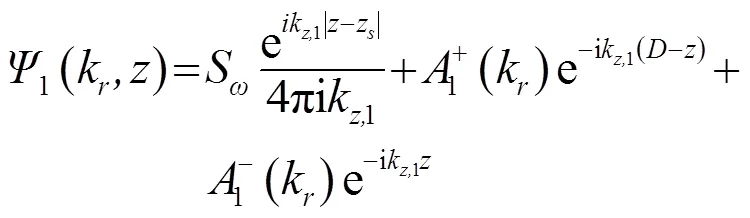
海底中格林函数与文献[12]一样,同样以海底界面为参考点。可求得系统方程:

为了解决该问题,本文提出一种避免数值溢出的计算方法,在每层中采用相对坐标,海水中的下行波以海面作为参考点,上行波以海底为参考点。此时:


可求得系统方程:
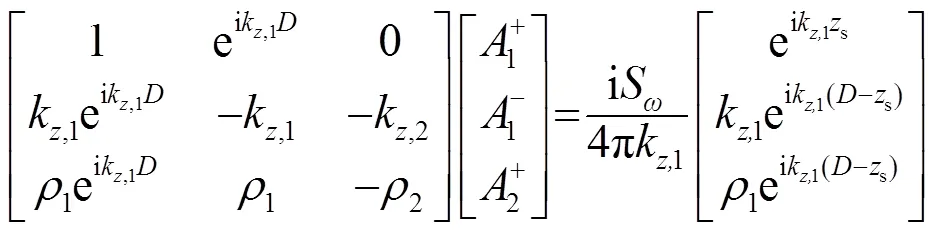
前文已经讨论过,点源问题与线源问题对格林函数的求解方法是一样的,所以以上讨论同样适用于线源。接下来对线源问题的声场计算以及仿真都是基于该数值稳定的解法。
1.3 格林函数解析解的验证


海底中深度格林函数的解析解为
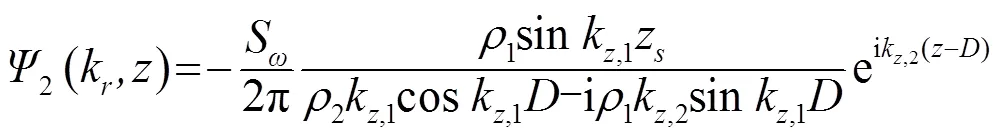
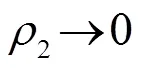
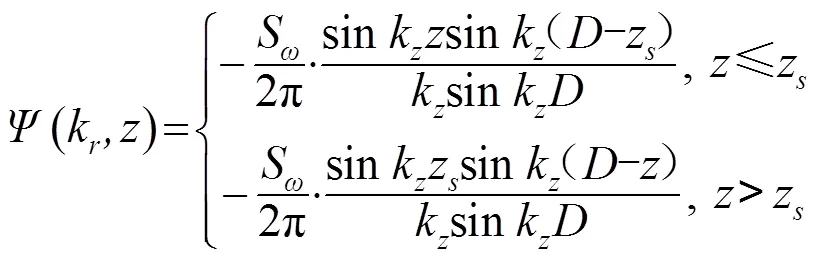
根据已有文献,将格林函数进行模式展开[14-15]:


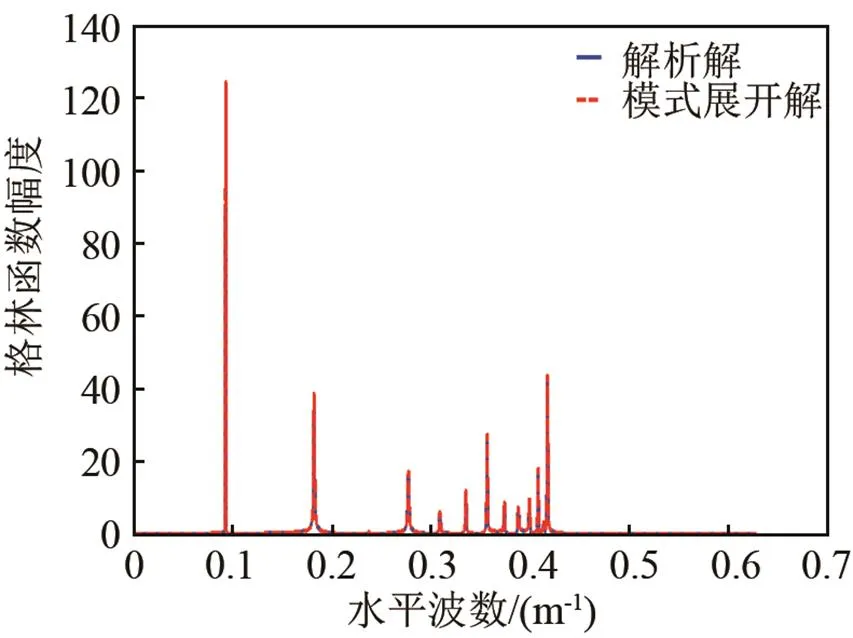
对该解析解进行验证,取海深为100 m,声源深度为36 m,接收器深度为46 m,频率为100 Hz。模式展开数分别取10以及50,将解析解的结果与格林函数模式展开结果做比对,结果如图2、图3所示。
通过比较图2、图3可以看出,当模式展开数较小的时候,格林函数的模式展开不能很好地反映求得的格林函数解析解;而当模式展开数足够大的时候,格林函数的模式展开可以很好地反映求得的格林函数解析解。因此,本方法求得的解析解的结果是无条件收敛的,该结果可以在后续的积分计算中直接代入使用。

(a) 格林函数
(b) 水深与格林函数幅度的关系
图2 模式展开数为10时,解析解结果与模式展开结果比较
Fig.2 Comparisonbetween model expansion result of Green’s function and analytical solution when model expansion number = 10
(a) 格林函数
(b) 水深与格林函数幅度的关系
图3 模式展开数为50时,解析解结果与模式展开结果比较
Fig.3 Comparison between model expansion result of Green’s function and analytical solution when model expansion number = 50
1.4 声场计算
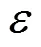
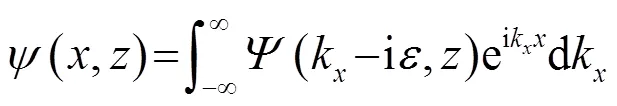

传播损失的计算遵循:


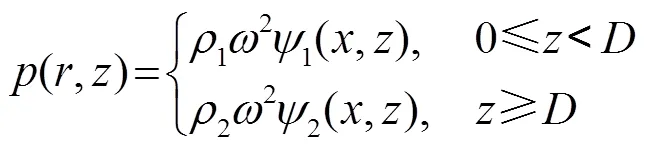
而

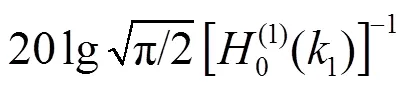
2 数值仿真
在第1节中给出了本方法中格林函数的解析解,可以通过该解析解代入傅里叶变换式中直接求解类似的Pekeris波导问题,将本文提出方法的结果与简正波标准程序KRAKENC[16]求得的结果作比较。选用两个仿真例子,验证本方法的精确度。
2.1 算例1
如图4所示,海面和海底是平行界面,海水声速为1 500 m/s,海底声速为1 800 m/s,海水密度为1 000 kg/m3,海底密度为1800 kg/m3,海底声吸收分两类情况,分别是无吸收海底,以及吸收系数为0.5 dB/的海底,水深为100 m。线源深度为36 m,平行于海面,接收器深度为46 m,声源频率为20 Hz。

图4 算例1中的Pekeris波导,声源为线源
图5给出该算例求得的深度格林函数,其中蓝色实线是无吸收海底情况下的深度格林函数,红色虚线是海底吸收系数为0.5 dB/情况下的深度格林函数。该算例下存在两号简正波,在图5中分别用1、2标记出来。该算例下,海底波数接近于第2号简正波水平波数,KRAKENC计算不出该号简正波,因而此时KRAKENC不能求解出正确的结果。需要指出的是,在KRAKEN模型的三个求解简正波的模型中(KRAKEN、KRAKENC和KRAKEL),我们使用的是KRAKENC。
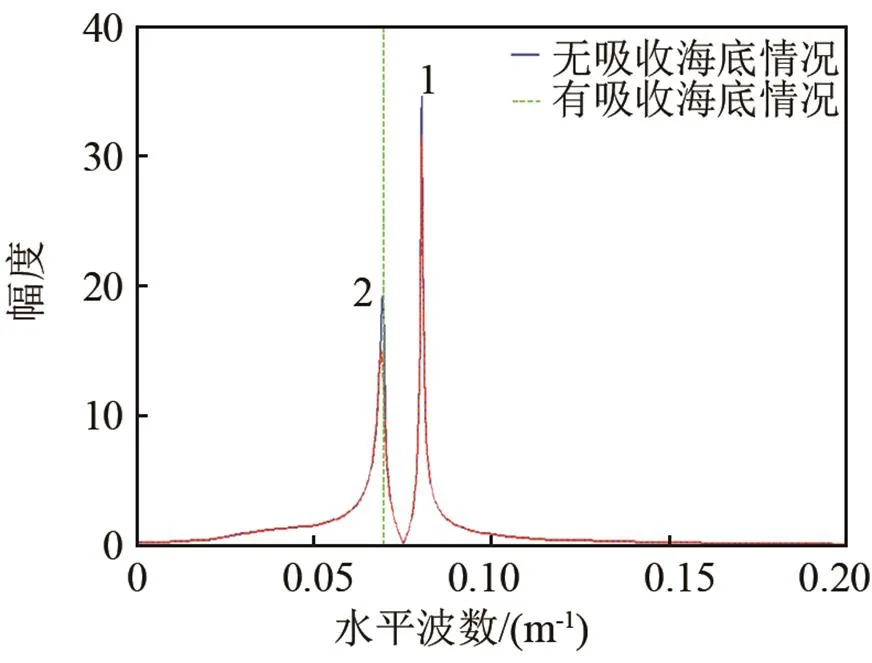
图5 算例1的深度格林函数
图6分别给出海底无吸收以及海底吸收系数为0.5 dB/情况下本文所用的方法与KRAKENC在0~15 km的结果比对。蓝色实线为本文所用方法的结果,红色虚线为KRAKENC的结果。由于第二号简正波水平波数与海底波数非常接近,KRAKENC计算不出该号简正波,因此KRAKENC计算的结果是不准确的。
图7分别是海底无吸收以及海底吸收系数为0.5 dB/λ情况下本方法得到的声场结果。

(a) 海底没有吸收
(b) 海底吸收系数为0.5 dB/
图6 两种不同方法计算的0~15 km传播损失
Fig.6 Transmission losses from 0 to 15 km computed by two different methods
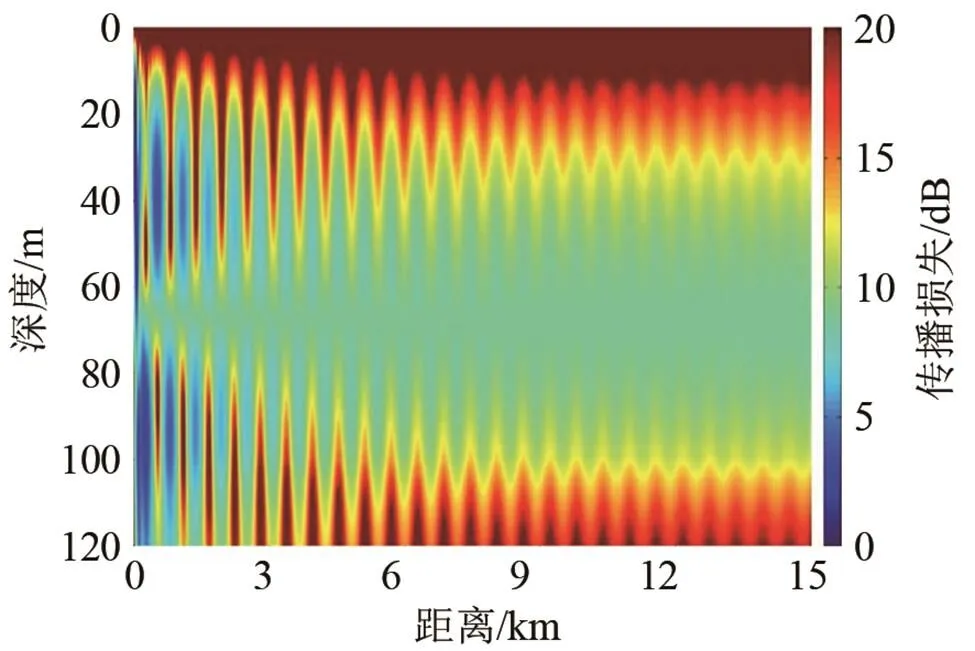
(a) 海底无吸收
(b) 海底吸收系数为0.5 dB/
图7 本方法得到的声场结果
Fig.7 Acoustic field computed by the present method
2.2 算例2

图8 算例2中的Pekeris波导问题,声源为线源
频率112 Hz与118 Hz的声场结果如图9所示。然后做出声源频率在105~125 Hz范围内的声场结果,如图10所示。在该算例下,当声源频率在112 Hz附近时候,KRAKENC计算的结果是不准确的。
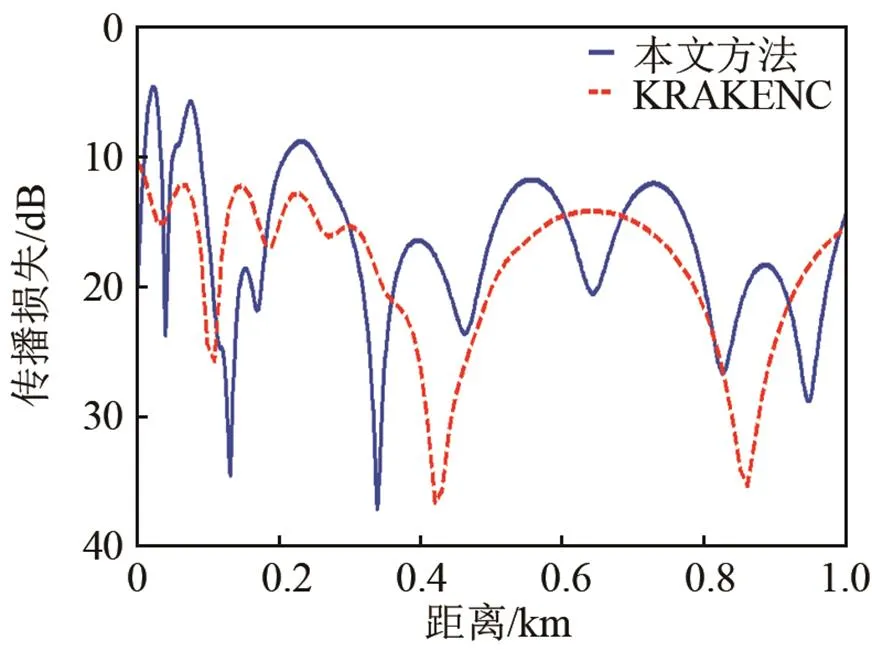
(a) 声源频率为112 Hz
(b) 声源频率为118 Hz
图9 两个不同频率的0~1 km传播损失曲线
Fig.9 Transmission loss curves from 0 to 1 km at two different frequencies

(a) 本方法的结果
(b) KRAKENC的结果
图10 两种方法计算的传播损失图
Fig.10 Transmission loss diagrams computed by two different methods
如图11所示,分别做出两个频率下的格林函数,同时,表1给出了KRAKENC计算的各号简正波的水平波数。可以看出,在该算例下,当频率为112 Hz时,海底波数近似相等于第三号简正波水平波数,从表1可以看出,在该频率下,KRAKENC没有计算出该号简正波,因此该频率下KRAKENC 计算的声场结果不准确。而当频率为118 Hz时,海底波数与各号简正波的水平波数能够明显区分出来,从表1可以看出,在该频率下,KRAKENC可以很好地求解出各号简正波,因此该频率下KRAKENC计算的声场结果是准确的。
(a) 声源频率为112 Hz
(b) 声源频率为118 Hz
图11 两个不同频率的深度格林函数
Fig.11 Depth-dependent Green’s functions at two different frequencies

表1 KRAKENC计算的不同频率下激发的简正波的水平波数
当距离增大时,做出声场结果,结果如图12所示。可以发现,本方法计算的结果与KRAKENC的结果的差异随着距离的增大而减小。由于KRAKENC某些情况下在近场计算上存在误差,因此本方法可以作为其在低频近场声场计算的有效补充。

(a) 频率112 Hz
(b) 频率118 Hz
图12 两个不同频率的0~15 km传播损失曲线
Fig.12 Transmission loss curves from 0 to 15 km at two different frequencies
3 结论
本文在给出线源声场中波数积分理论公式的基础上,从理论上分析了已有文献中不合理的归一化可能会导致的数值溢出问题,进而通过合理的参考深度值的选择,保持了系数矩阵方程解的数值稳定性,从而求得格林函数的解析解。同时本文将该解析解与格林函数的模式展开的结果做比较,验证了该解析解的正确性,因而以后类似问题的处理都可以直接用解析解代入计算,提高了计算效率。
本文通过两个算例将本方法与KRAKENC做了比较,结果表明,当某号简正波的水平波数接近于海底波数时,KRAKENC有可能计算不出这号简正波,这会导致KRAKENC计算不出正确的声场结果,而波数积分方法采用的是直接数值求积分的方法,因而不存在这种问题。因此,本文所提出的方法可以作为Pekeris波导中线源问题的标准模型来应用。
[1] Pekeris C L. Theory of propagation of explosive sound in shallow water[J]. Geological Society of America Memoirs, 1948, 27: 1-116.
[2] 布列霍夫斯基赫. 分层介质中的波[M]. 2版. 北京: 科学出版社, 1985.BREKHOVSKIKH L M. Waves in layered media[M]. 2ndEdition. Beijing: Science Press, 1985.
[3] 杨士莪. 水声传播原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 1994.YANG Shi’e. Theories of underwater sound propagation[M]. Harbin: Harbin Engineering University Press, 1994.
[4] 汪德昭, 尚尔昌. 水声学[M]. 北京: 科学出版社, 1981.WANG Dezhao, SHANG Erchang. Underwater acoustic[M]. Beijing: Science Press, 1981.
[5] LUO W, Schmidt H. Three-dimensional propagation and scattering around a conical seamount[J]. J. Acoust. Soc. Am., 2009, 125(1): 52-65.
[6] LUO W, Yang C, Qin J, et al. A numerically stable coupled-mode solution for sound propagation in range-dependent waveguides[C]// Meetings on Acoustics. American Institute of Physics, 2012: 313-320.
[7] Collins M D, Schmidt H, Siegmann W L. An energy-conserving spectral solution[J]. J. Acoust. Soc. Am., 2000, 107(4): 1964-1966.
[8] Collis J M, Siegmann W L, Jensen F B, et al. Parabolic equation solution of seismo-acoustics problems involving variations in bathymetry and sediment thickness[J]. J. Acoust. Soc. Am., 2008, 123(1): 51-55.
[9] Thompson L L. A review of finite-element methods for time- harmonic acoustics[J]. J. Acoust. Soc. Am., 2006, 20(3): 1315- 1330.
[10] Graves R, Nagl A, Uberall H, et al. Normal mode theory of underwater sound propagation in a range dependent environment [C]// Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP. IEEE, 1976: 668-670.
[11] 姚万军. 基于波数积分的水声传播建模实现方法研究[J]. 应用声学, 2008, 27(4): 288-293. YAO Wanjun. An approach to underwater acoustic propagation modeling based on wave-number integration technique[J]. Applied Acoustics, 2008, 27(4): 288-293.
[12] Schmidt H, Seong W, Goh J T. Spectral super-element approach to range-dependent ocean acoustic modeling[J]. J. Acoust. Soc. Am., 1995, 98(1): 465-472.
[13] Goh J T, Schmidt H. A hybrid coupled wave-number integration approach to range-dependent seismoacoustic modeling[J]. J. Acoust. Soc. Am., 1996, 100(3): 1409- 1420.
[14] Jensen F B, Kuperman W A, Porter M B, et al. Computational ocean acoustics[M]. Springer Science & Business Media, 2000.
[15] Jensen F B, Kuperman W A, Porter M B, et al. Computational ocean acoustics[M]. Springer Science & Business Media, 2011.
[16] Porter M B. The KRAKEN normal mode program[R]. NAVAL RESEARCH LAB WASHINGTON DC, 1992.
A wavenumber-integration method based solution to the acoustic field excited by a line source
YU Xiao-lin1,2, LUO Wen-yu1, YANG Xue-feng2,3, ZHANG Ren-he1
(1. State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. Shanghai Acoustics Laboratory, Chinese Academy of Sciences, Shanghai 201815, China)
An unconditionally stable computation method based on the wave-number integration method is presented for the acoustics field excited by a line source in a Pekeris waveguide. Both up and downgoing waves in the depth-dependent wave equation are appropriately normalized in order to obtain a stable coefficient matrix. Analytical solution to the depth-dependent Green’s function is also presented. Modal expansion of the Green’s function is performed to validate the analytical solution. It indicates that the analytical solution is accurate. The transmission loss calculated by this method is compared with those given by KRAKENC with an example. It shows that when a certain mode is close to the bottom wavenumber, KRAKENC fails to find this mode. As a result, the field result by KRAKENC is inaccurate. However, the wavenumber-integration method suits well for such problems. Numerical results indicate that the present model can serve as a benchmark model for the problem of sound propagation excited by a line source in a Pekeris waveguide.
line-source problem; wavenumber integration; numerically stable solution
TB556
A
1000-3630(2017)-05-0415-08
10.16300/j.cnki.1000-3630.2017.05.004
2016-11-04;
2017-02-15
国家自然科学基金资助项目(11434012、41561144006)
于晓林(1990-), 男, 山东威海人, 博士研究生, 研究方向为水声物理。
于晓林, E-mail: asd982209895@126.com

