水下蜂窝空腔覆盖层的隔声性能分析

唐世灏，叶韩峰，陶猛，李政杰



水下蜂窝空腔覆盖层的隔声性能分析

唐世灏1，叶韩峰2，陶猛2，李政杰1

(1. 贵州大学现代制造技术教育部重点实验室，贵州贵阳 550025；2. 贵州大学机械工程学院，贵州贵阳 550025)

针对驻波管隔声量测试过程中，透射管末端反射波难以消除并对测试结果有一定影响的问题，利用LMS Virtual.lab有限元软件建立了驻波管隔声量测试的仿真模型。在模型中设置无反射边界条件，基于该模型分析了蜂窝空腔覆盖层的隔声性能，指出蜂窝空腔覆盖层的隔声特性是阻抗失配、波型转换、阻尼损耗等多种机理共同作用的结果，蜂窝结构的胞元壁厚、胞元夹角、黏弹性材料的杨氏模量等参数变化对隔声量的影响较为明显。消除了入射管端面和透射管端面的反射波，并通过与解析方法的计算结果对比验证了模型的正确性。

蜂窝空腔；黏弹性覆盖层；隔声量；三传声器法

0 引言

敷设在水下目标表面的多种声学覆盖层，通常具有吸声、隔声、抑振或抗冲击等功能，是目前唯一能够同时有效对抗主、被动探测的关键技术。声学覆盖层通常是含有各种空腔结构如球形、柱形空腔[1-2]，或填充了局域共振单元[3-4]的黏弹性复合结构。这些结构在具有良好吸声性能的同时，也兼具了其他功能，例如圆柱空腔覆盖层具有一定的隔声特性[5]和抗冲击特性[6]。

蜂窝结构由于具有较高的强度和较好的耐冲击等特点，在许多领域得到了极广泛的应用。在噪声控制方面，Ruzzene[7]采用有限元方法研究了蜂窝结构梁在空气中的振动声辐射特性。赵颖坤[8]等人运用传递矩阵方法和声能面积百分比的观点，分析了水下蜂窝夹层结构的透射系数和隔声量，得出蜂窝夹层结构的隔声性能整体要比相同厚度条件下的圆孔橡胶层、均匀橡胶层好。这种结构的蜂窝空腔是垂直于上、下面板布置的，与传统的圆柱空腔覆盖层[2]从结构形式上来说是类似的，但是这类结构在静压作用下的变形较大，并且对声学性能有较大影响。改变空腔的布置方式，即将覆盖层中的空腔由垂直于面板布置改为平行于面板水平布置，静水压力变化对覆盖层声学性能的影响较小[9]。

本文对水平排列的蜂窝空腔结构黏弹性覆盖层的水中隔声特性开展研究，基于驻波管中三传声器法测量隔声量的原理，利用LMS Virtual.Lab软件建立蜂窝空腔覆盖层的隔声量计算模型，并在此基础上分析了蜂窝空腔覆盖层的结构参数、黏弹性材料属性对隔声特性的影响，比较了低频隔声和中高频隔声机理的不同。

1 驻波管隔声量测试原理

实际的驻波管隔声量测试通常采用四传声器方法[10]，这是因为驻波管透射段的吸声末端很难实现完全吸声，因此不可避免地在透射段中存在末端反射波，这对测试结果的准确性有一定影响。采用有限元方法仿真驻波管隔声量测试，可以有效消除末端反射波的影响，这是因为在有限元软件或者有限元方法中可以设置透射段末端为完全吸声边界，即不存在末端反射。因此，只需在透射管中设置一个传感器即可直接测得透射波声压，本文接下来的仿真分析都是基于三传声器法分析隔声量。

图1 阻抗管中三传声器法的测量系统示意图

Fig.1 Schematic diagram of three-microphone measuring system in a standing-wave tube

根据入射波和透射波可以计算隔声量：

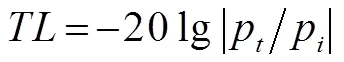
2 有限元计算模型及验证

第1节的分析指出，仿真的关键是获取三个传声器位置的声压值。利用LMS Virtual.lab软件计算材料的透射系数或隔声量，需要建立结构有限元模型和声学有限元模型，定义材料参数和网格属性，设置约束边界条件和声源激励方式。特别是该软件中可以直接定义杨氏模量损耗因子，这对分析黏弹性材料的损耗特性尤为方便。此外，由于水介质与蜂窝结构基体材料的特性阻抗相差不大，在界面上存在结构振动和声传播的耦合作用，因此采用Acoustics模块下的直接声振(Direct Vibro-Acoustic，DVA)耦合计算方法。

利用LMS Virtual.lab软件，建立了图2所示的有限元分析模型，其中驻波管为矩形波导形式，平面波从入射管一侧垂直入射到样品前表面。由于本文研究对象是平面波垂直入射无限大结构层的隔声性能，因此在样品四个侧面处施加对称约束形式。为了消除入射管端面1和透射管端面2的反射波，保证驻波管中仅存在一次入射波、一次反射波和一次透射波，在两个端面处设置无反射边界条件，这在软件中可以直接定义。

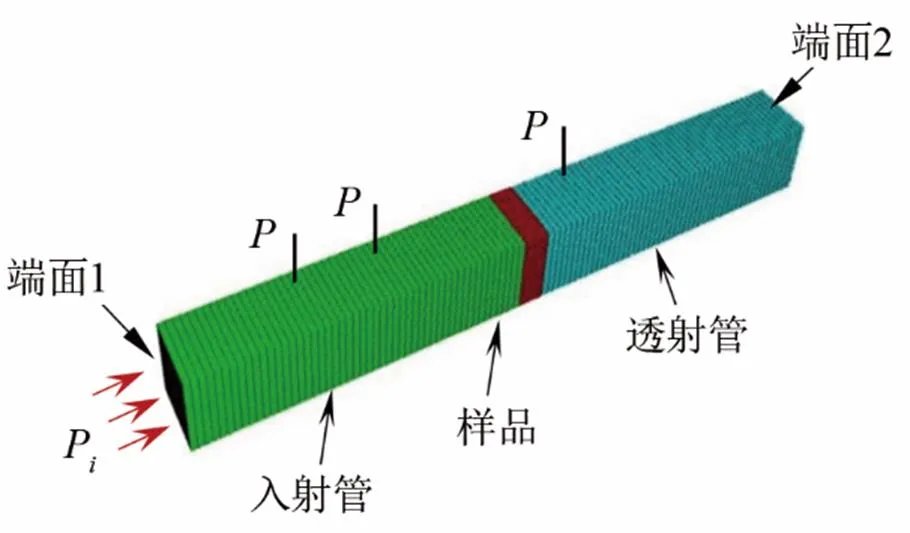
图2 隔声量计算的LMS Virtual.lab有限元模型

图3是二维理论解和有限元结果的比较，从图3中可以看出，二者在中高频率误差稍有增加。这是因为二维理论对变截面圆柱空腔的处理，采用了多段均匀截面圆柱空腔组合来代替。当频率增加以后，这种近似代替与实际模型的差异也逐渐体现出来。此外，二维理论认为圆柱空腔封口层的反射系数为1，而有限元模型是根据实际形状建模，这也是引起两者计算结果不同的原因之一。尽管如此，两种方法的计算结果整体来说符合良好，说明了本文建立的有限元模型的正确性。

图3 圆柱空腔覆盖层吸声系数的理论解和数值解比较

3 蜂窝空腔覆盖层隔声性能分析

图4 蜂窝空腔覆盖层结构示意图

3.1 胞元壁厚的影响

在蜂窝空腔覆盖层的胞元大小不变的情况下，胞元壁厚改变对隔声性能的影响是值得关注的问题。图6给出了胞元壁厚不同时，蜂窝空腔覆盖层的隔声量曲线，其中壁厚分别为1.0、0.8、0.6 mm。从图6中可以看出，胞元壁厚越小，蜂窝空腔覆盖层的隔声量越大。这可以从阻抗失配的角度来解释，胞元壁厚越小表示空腔所占比例越大，也就意味着蜂窝空腔覆盖层与外部水介质的阻抗失配程度越大，导致声波入射到蜂窝空腔覆盖层表面时被反射的能量增加，而能够进入蜂窝空腔覆盖层并透射至另一侧水介质的能量减小，因此增加了隔声量。

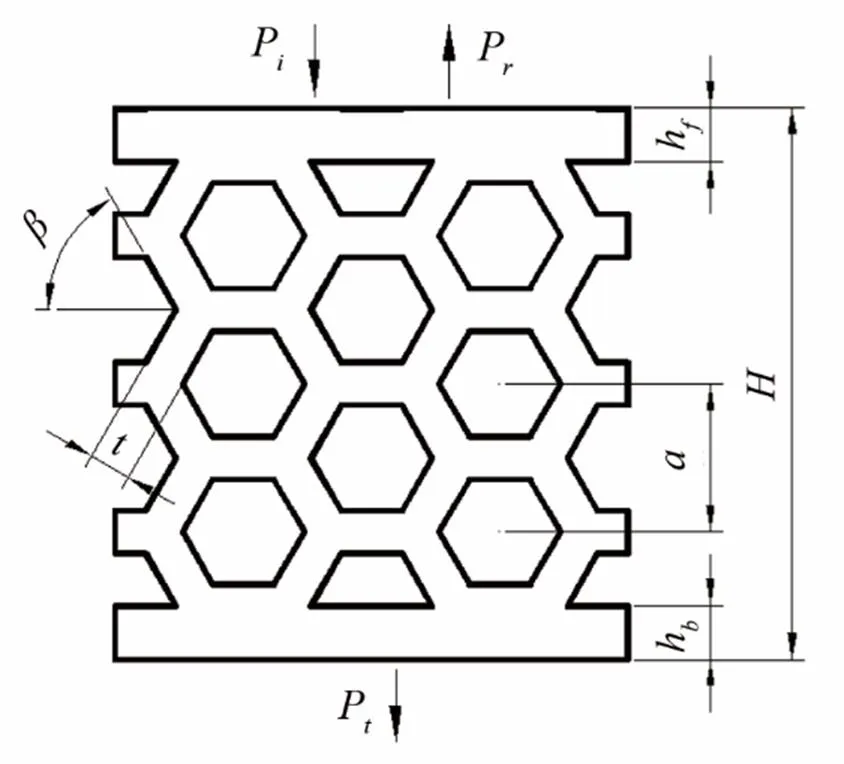
图5 蜂窝空腔覆盖层截面示意图

图6 胞元壁厚不同，蜂窝空腔覆盖层的隔声量

3.2 胞元夹角的影响

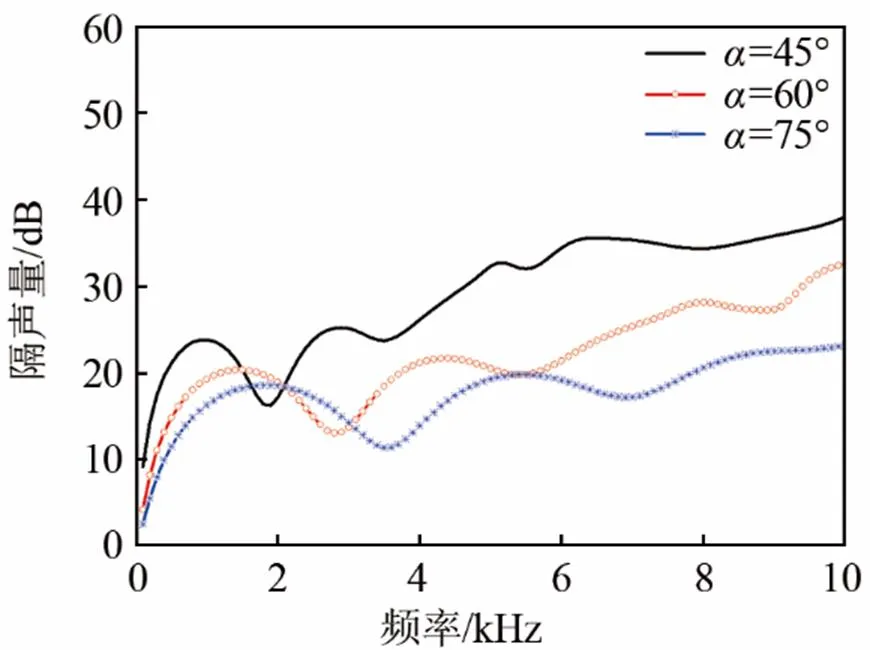
图7 胞元夹角不同，蜂窝空腔覆盖层的隔声量

图8是950 Hz平面波垂直激励时，45°胞元夹角的蜂窝空腔覆盖层的位移云图，该频率对应隔声量曲线的第一个极大值。从图8可以看出，蜂窝空腔结构中部的纵向振动占主导地位，导致能量损耗较大，当弹性波传播到蜂窝结构层后表面时，激起的后表面振动幅度有限，因此隔声量达到最大。

图9是6 500 Hz的位移云图，该频率对应隔声量曲线的第四个极大值，中高频段的极大值与低频范围的极大值的特点有所不同，此时蜂窝空腔覆盖层不是以整体的纵向振动为主，而是既有纵向振动、又有明显的横向振动，呈现出波型转换的特点，由于横向振动的损耗因子远大于纵向振动，因此中高频范围的隔声量数值达到30 dB以上。

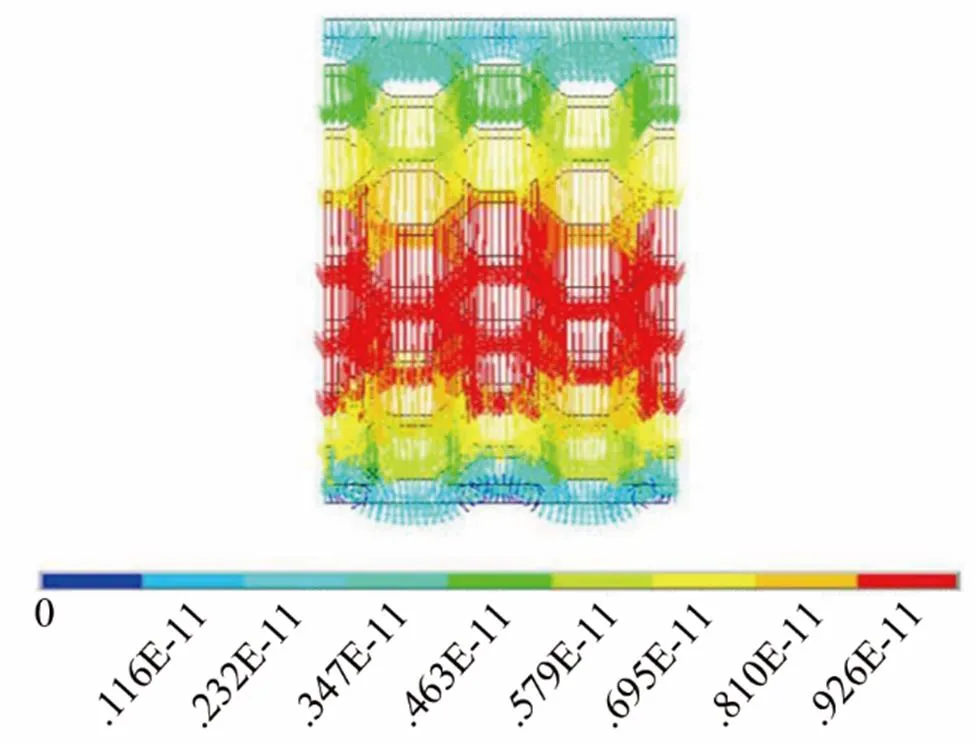
图8 蜂窝空腔覆盖层的位移云图(950 Hz)

图9 蜂窝空腔覆盖层的位移云图(6 500 Hz)

3.3 杨氏模量的影响

图10给出了不同的基体材料杨氏模量条件下蜂窝空腔覆盖层的隔声量曲线，其中杨氏模量分别为100、160和250 MPa。从图10中可以看到，基体材料的杨氏模量对蜂窝空腔覆盖层的隔声性能有较大影响：第一，较小的杨氏模量对应传播声速较低，因此隔声量曲线的振荡起伏周期减小；第二，传播声速较低引起基体材料与水介质的阻抗失配程度增加，因此隔声量曲线随杨氏模量的减小而增加；第三，由于考虑了基体材料的黏弹性损耗，隔声量曲线振荡幅度随频率的增加而逐渐减小。

图10 杨氏模量不同，蜂窝空腔覆盖层的隔声量

3.4 损耗因子的影响

图11给出了不同损耗因子条件下，蜂窝空腔覆盖层的隔声量曲线，其中损耗因子分别为0.2、0.3和0.4。基体材料的损耗因子对蜂窝空腔覆盖层的隔声量周期影响不是很大，这是因为损耗因子的改变对基体材料中的传播声速基本没有影响，但是损耗因子越大，引起的传播衰减相应越大，因此增加损耗因子更多地降低了隔声量曲线振荡起伏的程度，也就是说起到了削峰填谷的作用。从图11中不难看出，损耗因子为0.4时对应的蜂窝空腔覆盖层隔声量达到最大，反应出增加损耗因子对于提高蜂窝空腔覆盖层隔声性能的重要性。

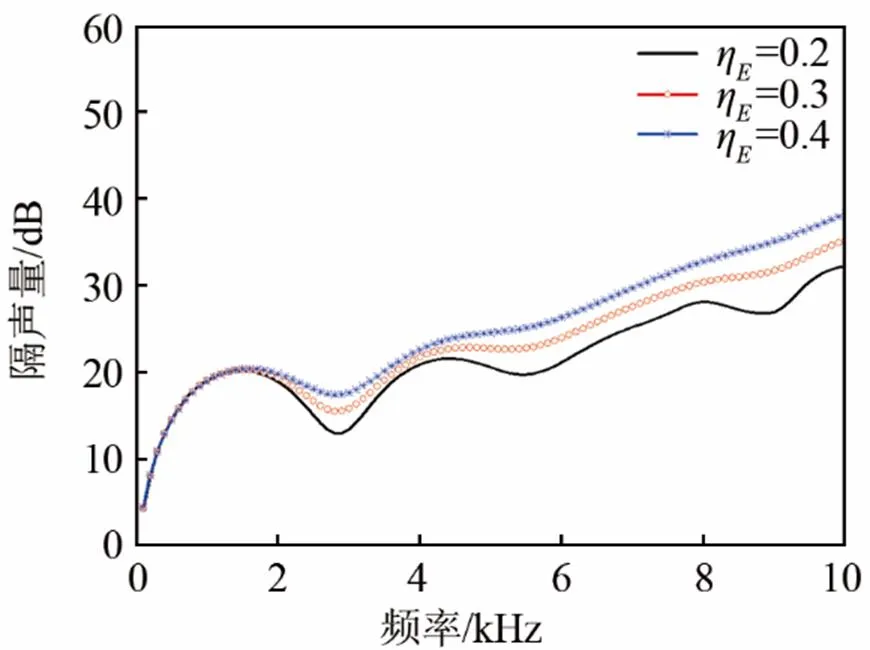
图11 不同损耗因子时，蜂窝空腔覆盖层的隔声量

4 结论

基于驻波管中隔声量测试方法，本文利用LMS Virtual.Lab软件建立了蜂窝空腔覆盖层隔声量计算的有限元模型，并通过与解析方法的计算结果对比验证了计算模型的正确性。在此基础上，分析了结构参数和材料属性对蜂窝空腔覆盖层隔声量的影响，得出：(1) 蜂窝空腔覆盖层的隔声特性是阻抗失配、波型转换、阻尼损耗等多种机理共同作用的结果；(2) 蜂窝结构的胞元壁厚、胞元夹角，黏弹性材料的杨氏模量等参数变化对蜂窝空腔覆盖层隔声量的影响较为明显。

[1] Ivansson S M. Anechoic coatings obtained from two- and three-dimensional monopole resonance diffraction gratings[J]. J. Acoust. Soc. Am., 2012, 131(4): 2622-2637.

[2] 何世平, 汤渭霖, 何琳, 等. 变截面圆柱形空腔覆盖层吸声系数的二维近似解[J]. 船舶力学, 2006, 10(1): 120-127. HE Shiping, TANG Weilin, HE Lin, et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity[J]. Journal of Ship Mechanics, 2006, 10(1): 120-127.

[3] Jiang H, Wang Y R, Zhang M L, et al. Wide-band underwater acoustic absorption based on locally resonant unit and interpenetrating network structure[J]. Chinese Physics B, 2010, 19(2): 026202.

[4] ZhaoH G, Wen J H, and Yang H B. Backing effects on the underwater acoustic absorption of a viscoelastic slab with locally resonant scatterers[J]. Applied Acoustics, 2014, 76: 48-51.

[5] Panigrahi S N, Jog C S, Munjal M L. Multi-focus design of underwater noise control linings based on finite element analysis[J]. Applied Acoustics, 2008, 69(12): 1141-1153.

[6] 汪玉, 钱德进, 曾令玉, 等. 隔声去耦瓦抗冲击性能数值研究[J]. 中国舰船研究, 2009, 4(3): 1-7. WANG Yu, QIAN Dejin, ZENG Lingyu, et al. Numerical study on the anti-shock capability of acoustic insulated and decoupled tiles[J]. Chinese Journal of Ship Research, 2009, 4(3): 1-7.

[7] Ruzzene M. Vibration and sound radiation of sandwich beams with honeycomb truss core[J]. Journal of Sound and Vibration, 2004, 277(4): 741-763.

[8] 赵颖坤, 盛美萍, 王朝杰, 等. 水中蜂窝夹层结构的隔声性能[J]. 机械科学与技术, 2006, 25(6): 745-747. ZHAO Yingkun, SHENG Meiping, WANG Chaojie, et al. Sound insulation properties of underwater honeycomb truss structures[J]. Mechanical Science and Technology, 2006, 25(6): 745-747.

[9] Tao M, Jiang K, Wang K P, et al. Sound insulation performance of viscoelastic coating which contains horizontally-distributed cylindrical holes[C]//International Conference on Materials Engineering and Industrial Applications. Hong Kong, 2015: 9-14.

[10] 曲波, 朱蓓丽. 驻波管中隔声量的四传感器测量法[J]. 噪声与振动控制, 2002, 22(6): 44-46. QU Bo, ZHU Beili. Four-microphone method of sound transmission in the standing wave tube[J]. Noise and Vibration Control, 2002, 22(6): 44-46.

[11] 朱蓓丽, 罗晓辉. 驻波管中的隔声量测试方法[J]. 噪声与振动控制, 2000, 20(6): 41-43. ZHU Beili, LUO Xiaohui. Measurement of the sound transmission loss in the standing wave tube[J]. Noise and Vibration Control, 2000, 20(6): 41-43.

[12] 朱蓓丽, 肖今新. 双水听器传递函数法低频测试及误差分析[J]. 声学学报, 1994, 19(5): 351-360. ZHU Beili, XIAO Jinxin. A two-hydrophone transfer function method for measuring low-frequency acoustic properties and its error analysis[J]. Acta Acustica, 1994, 19(5): 351-360.

Sound insulation performance of underwater honeycomb cavity covering

TANG Shi-hao1, YE Han-feng2, TAO Meng2, LI Zheng-jie1

(1. Key Laboratory of Advanced Manufacturing Technology, Ministry of Education, Guizhou University, Guiyang 550025, Guizhou, China;2. School of Mechanical Engineering, Guizhou University, Guiyang 550025, Guizhou, China)

Because the reflected wave from the downstream tube can not be totally eliminated in the standing-wave tube, which would affect the accurate measurement of sound transmission loss, the simulation model of measuring sound transmission loss in the standing-wave tube is presented by usingLMS Virtual.lab software. The non-reflected boundary conditions are defined in the present model. Then, the sound insulation performance of honeycomb cavity covering is analyzed and discussed based on the present model. It is summarized that the mechanism of sound insulation performance includes impedance mismatch, waveform transformation and damping loss. Moreover, the effects of the cell thickness, cell angleand viscoelastic Young’s modulus of the honeycomb structure on the sound insulation performance of honeycomb cavity covering are more obvious. The present model has been validated by comparing the numerical results of the analytical method, which can eliminate the reflected waves from the end surfaces of the upstream tube and the downstream tube.

honeycomb cavity; viscoelastic covering; sound transmission loss; three-microphone method

TB 564

A

1000-3630(2017)-05-0437-05

10.16300/j.cnki.1000-3630.2017.05.007

2016-10-14;

2016-12-10

国家自然科学基金项目(51365007、51765008); 贵州省高层次创新型人才培养项目(黔科合人才[2016]4033)

唐世灏(1989－), 男, 贵州六盘水人, 硕士研究生, 实验师, 研究方向为机械制造及其自动化。

陶猛, E-mail: 29720834@qq.com