驻波教学中的初相问题

魏巧 汤朝红

(武汉工程大学理学院 湖北 武汉 430073)

1 引言

驻波是大学物理教学中的重、难点内容，在教学中我们发现，学生一般不易正确理解驻波.其中，用以形成驻波的入射波和反射波的初相就是一个容易产生困扰的问题.

在一般的大学物理教材[1,2]中，通常先给出弦线驻波的实验，如图1所示.通过观察实验得到波的状态和特征，从而引入驻波的概念，让学生有一个感性认识.然后分析实验过程.我们知道,因为入射波在反射端反射后得到反射波，入射波和反射波在同一根弦上相向传播，在适当的弦长下就会叠加得到驻波.接着，引入简谐波的波动方程，对驻波进行定量描述，进而得到驻波方程以及波节和波腹的位置.

图1 弦线驻波实验

2 驻波方程和初相

为了讨论的方便，常常选取一个特殊的空间位置(某一波腹)作为x轴原点，选取一个特殊时刻(原点处质点达到正向最大位移)作为计时起点，于是就有两列波的初相φ1=φ2=0.所以,驻波方程为

(1)

其中

(2)

(3)

这样处理会使得到的驻波方程简单明了，但如果学生不做深入思考则会认为式(1)是驻波的一般形式，误以为φ1=φ2=0是必须满足的条件，而遇到初相不为零的情况就不知所措了.

现在考察一下驻波的定义,驻波是由振幅、振动方向、频率和传播速度都相同的两列相干波，在同一方向上沿相反方向传播时叠加而成的一种特殊形式的干涉现象.显然，上述定义对两列波的初相并没有要求.对于任选坐标原点和计时起点的一般情况，设

(4)

(5)

利用和差化积公式，驻波方程为

(6)

在波节处

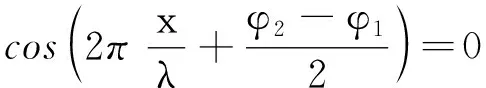
(7)

所以,波节位置为

(8)

(k=0,±1,±2,…)

同理，在波腹处

(9)

得波腹位置

(10)

(k=0,±1,±2,…)

例如，假设图1的驻波实验中入射波方程为

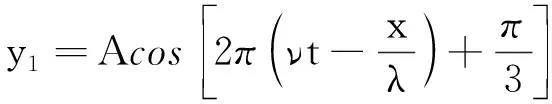
(11)

(12)

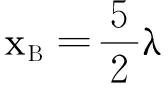
(13)

得

φ2=φ1+(2k-9)π

(14)

取k=5，则

(15)

显然，在B点存在着半波损失.此时，驻波方程为

(16)

总之，通过对一般驻波方程的讨论和推导，可以使学生深入了解入射波和反射波的相位在驻波问题中所扮演的角色，有助于正确地理解驻波的物理本质.

参考文献

1 程守洙, 江之永．普通物理学3(第五版)．北京：高等教育出版社，1998. 132～138

2 马文蔚．物理学(下册 第四版)．北京：高等教育出版社，1999. 67～72