由“动量 动量守恒定律”教学引发的思考

曾令锋

（梅县丙村中学 广东 梅州 514762）

动量定理与动量守恒定律在高中阶段的物理教学中具有重要地位.经过高一一年的学习，学生已能够较好地运用牛顿运动定律和功能关系解决恒力作用下的力学问题，但碰到变力作用的情况，就会束手无策.即使一些思维能力较强的学生，也许能大概判断出物体在变力作用下的运动状态变化情况，也无法进行定量的分析与计算.动量定理和动量守恒定律将成为他们解决这类问题的“利器”.因此，如何上好“动量 动量守恒定律”一课，就显得尤为重要了.

在本节课的学习中，学生经常会被以下问题困扰，一是到底“动量”是什么？二是动量定理和牛顿第二定律有什么不同？三是动量守恒定律和动量定理之间有怎样的关联？学生的问题引起笔者深深的思考.

1 “动量”到底是什么

“动量”的概念，最早是由伽利略、笛卡儿等人在研究打击、碰撞的问题中提出来的，后来牛顿的工作使其更为完善.起初，它被称为“运动量”、“运动的量”，或者干脆简称为“运动”.如牛顿在《论物体的运动》一文手稿中写道，“……动力与加速的力之比等于运动与速度之比……”，文中“加速的力”指的是加速度，“运动”指的是动量.在《教师教学用书物理·选修3-5》［1］中也有这样一句话，“动量是描写物体运动量大小的，是描述物体机械运动状态的物理量.”如果就这样向学生介绍动量的物理意义，学生会产生新的疑问：“运动量”又是什么？是不是像人跑步一样，消耗的能量多，运动量就大？描述物体机械运动状态的物理量有很多，如“速度”描述运动快慢，“加速度”描述速度变化快慢，“动能”描述物体因运动而具有的能量，那“动量”描述什么呢？

其实，牛顿等人所提到的“运动”是一个复合的概念，它既涉及物体的质量，又与运动的快慢和方向有关.为了帮助学生更好地理解，我们向学生提两个问题：

（1）A，B两辆车，质量相同，A的速度远大于B，在相同情况下，哪辆车更容易停下来？哪辆车更容易转急弯？

（2）一辆小汽车和一辆装满货物的重型大货车，以相同的速度行驶，在受力相同的情况下，哪辆车更易停、更易转弯？

答案是很明显的.由此可以认为，运动物体的质量越大、速度越大，则在运动方向上的运动趋势越难被改变.

这个判断可由动量定理佐证.假设运动物体质量为m，速度为v，动量为p＝mv.要改变物体在运动方向上的运动趋势，有两种做法，一是使物体停止；二是在保持物体速率不变的前提下，使其速度方向转过一个极小的角度.如果采用第一种做法，由动量定理可知所需冲量大小为

如果用第二种做法，假设速度方向转过的角度为dθ，如图1，则所需冲量大小为

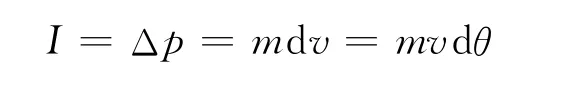
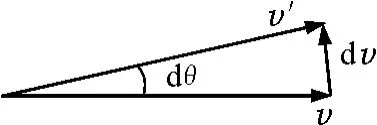
图1

结果表明，不论采取哪种做法，对于动量较大的运动物体，要改变其在运动方向上的运动趋势，均需要更大的冲量.

因此，动量的物理意义可以这样阐述，动量是一个描述运动物体在其运动方向上保持运动趋势的能力的物理量.

2 牛顿第二定律与动量定理的关系

在高中物理教材中，动量定理是由牛顿第二定律推导出来的，在物理学的发展史上也确实如此.

牛顿的三大运动定律是他在前人工作的基础上概括、总结出来的.1687年出版的《自然哲学的数学原理》［2］一书中，有关第二定律的正式表述为，“运动的变化正比于外力，变化的方向沿外力作用的直线方向.”（见书中定律Ⅱ）.根据这个表述可知其表达式应为

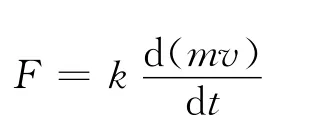
当F，m，v，t取合适的单位时，可使比例系数k＝1，上式可表示为

可见，牛顿第二定律的正式表述（文中称之为表述1）是基于动量变化的.这与高中物理教材中基于加速度的表述（本文中称之为表述2）有很大不同.而在高校的普通物理教材中采用的正是这种表述.那表述2的依据又是什么呢？这也可以在《自然哲学的数学原理》一书中找到答案.该书表述为，“……运动力由加速力与物质的量的乘积决定.”其中“运动力”指的是合外力，“加速力”指的是加速度，“物质的量”指的是质量.根据这个表述，可写出表达式

在F，m，a选取合适的单位使k＝1后可表示为

现在我们知道，式（1）适用于相对论，而式（2）只在经典力学中成立.牛顿选择表述1作为第二定律的正式表述，在那个力学研究对象只限于宏观、低速运动物体的年代，充分体现了一个伟大科学家的远见卓识.

有了牛顿第二定律，动量定理的提出就水到渠成了.在高中物理教材中，动量定理是基于传感器实验，由牛顿第二定律（表述2）导出的，过程如下.

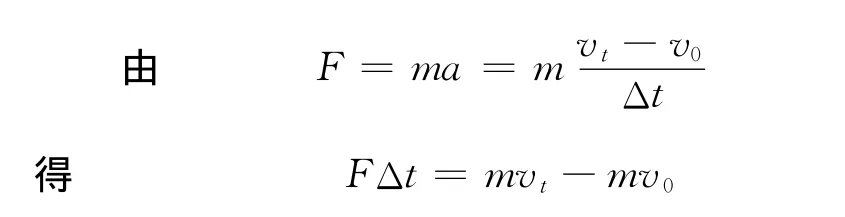
这种推导过程易被高中生接受，但无疑是不严谨的.因为该推导仍囿于恒力作用的思路，也难免会让善于思考的学生感到疑惑.而由表述1导出的过程则很好地解决了变力作用的问题，过程如下.

由式（1）得

两边积分，得

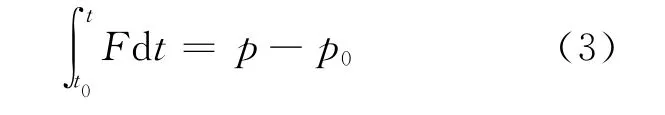
定义

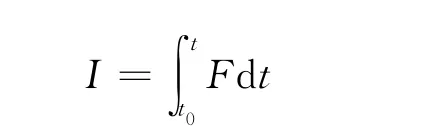
式（3）表示为

若质量m不变，式（4）又可写为

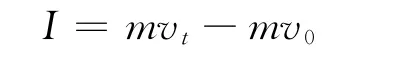
由此可见，牛顿第二定律是动量定理的基础，动量定理是根据牛顿第二定律推导出来的.但能否据此认为，动量定理与牛顿第二定律本质上是相同的，动量定理只是牛顿第二定律的另一种表达呢？

答案当然是否定的.从以上动量定理的推导过程中可以很清楚地知道，动量定理研究的是，物体在一段时间的受力与运动变化的关系，关注的是始末状态的变化.而在牛顿第二定律的表达式（1）中，出现了“dt”，代表时间t→0，说明牛顿第二定律研究的是物体受力瞬间的运动状态变化，具有瞬时性.这是两者最大的区别所在.

在高中物理阶段，两者的不同还体现在适用条件方面.高中阶段的牛顿第二定律为表述2，表达式为式（2），这种表述只适用于低速运动、宏观的物体.而动量定理除适用于宏观、低速的物体外，还适用于微观、高速的物体.另外，用牛顿第二定律的这种表述分析变力作用的情况，会碰到极大的困难，而动量定理则不存在这个问题.

可见，牛顿第二定律与动量定理，既有密切联系，又有明显区别，不可相互替代.

3 动量守恒定律与动量定理之间的关联

其实在科学史上，动量守恒思想的提出是远远早于牛顿第二定律的.早在古希腊时代，以德谟克利特为代表的原子论者就提出，运动只能由一个物体向另一个物体转移，但绝不会完全消灭.而笛卡儿则在《哲学原理》第二章中，第一次明确提出了动量守恒即物质和运动的总量永远保持不变.先贤们的思想是在观察、研究物体运动的过程中产生的，起初只是模糊的经验，后来被实验所证实.所以，动量守恒定律是实验性规律.因此，在高中物理教材中，动量守恒定律在学生实验的基础上被总结出来，是符合认知规律的.

另一方面，动量守恒定律也是动量定理必然导致的结果.讲清楚动量定理和动量守恒定律之间的逻辑推理关系，对于学生构建系统的知识体系，还是非常必要的.

教材中并未明确表明动量定理适用于两个或多个物体构成的系统，因此，有必要先对教材内容作适当的补充.举下面的例子.

【例题】如图2，光滑水平面上有两个带正电的小球A和B，小球A，B在水平向右的推力F作用下均向右运动.不考虑其他影响.求经时间t后，A，B的动量变化量之和.

图2

图3

解析：分析A，B球受力如图3，图中FAB，FBA为A，B球之间的平均作用力.据动量定理，对A有

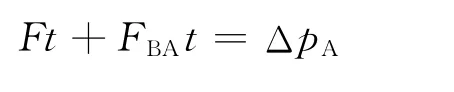
对B有

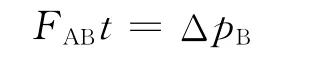
据牛顿第三定律

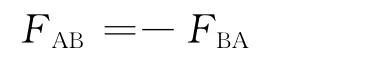
由以上各式得

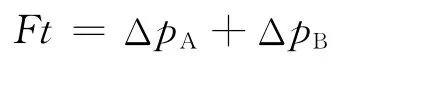
由此可知，系统所受合外力的冲量等于系统内各物体动量变化量之和，也就是等于系统总动量的变化量.当系统所受合外力为零时，系统总动量的变化量亦为零，即系统的总动量守恒.这就是动量守恒定律.

总之，牛顿第二定律、动量定理、动量守恒定律之间存在着密切的关系.对于它们之间的联系与区别，作为中学物理教师，只有清楚地知道其来龙去脉，才能更好地为学生答疑解惑.

1 广东基础教育课程资源研究开发中心物理教材编写组.教师教学用书物理·选修3-5.广州：广东教育出版社，2005.14～20

2 （英）伊萨克·牛顿著.自然哲学之数学原理.王克迪译.西安：陕西人民出版社，2001.9～19

3 赵凯华，罗蔚茵.新概念物理教程·力学.北京：高等教育出版社，1995.42～57