GBM 倾向评分加权法用于因果推断的研究＊

杨 伟，唐进法，易丹辉，李学林＊＊，李伟霞，周晓华

（1.中国中医科学院中医临床基础医学研究所 北京 100700；2.中央民族大学理学院 北京 100081；3.河南中医药大学第一附属医院 郑州 450000；4.中国人民大学应用统计科学研究中心北京 100872；5.北京大学北京国际数学研究中心 北京 100871）

GBM 倾向评分加权法用于因果推断的研究＊

杨 伟1,2，唐进法3，易丹辉4＊＊，李学林3＊＊，李伟霞3，周晓华5

（1.中国中医科学院中医临床基础医学研究所 北京 100700；2.中央民族大学理学院 北京 100081；3.河南中医药大学第一附属医院 郑州 450000；4.中国人民大学应用统计科学研究中心北京 100872；5.北京大学北京国际数学研究中心 北京 100871）

目的：在观察性研究或非随机化试验中，由于混杂因素＊＊＊的存在，研究人员从数据中进行因果推断的能力受到阻碍，本研究利用GBM倾向评分加权法对一组观察性医学数据进行了分析，以期指导相关医学人员进行他们自己的因果推断研究。方法：目前，四类主要的倾向评分法：匹配、分层、逆概率加权和混杂变量调整，已经被普遍用于因果推断的研究。倾向评分法理论上是可以消除可观测到的混杂因素的偏倚，使处理变量接近随机分配设计的效果，从而达到估计处理因素对结局因果效应的目的。结果：考虑到逆概率加权法相对于其它方法的优势，本文概括了它用于因果效应估计的适用条件，特别说明了运用一个现代多元非参数统计技术——广义Boosted模型(GBM)倾向评分加权法的关键环节及优劣。结论：当存在大量不同类型的混杂因素且它们与处理因素之间的线性、非线性或交互效应等函数形式无法确定以及其它问题的时候，GBM倾向评分加权法能克服在精确地估计倾向评分过程中所受到的阻碍，并给出相对更加接近于随机化的因果效应。

GBM 倾向评分加权 因果推断 观察性研究 非随机化试验

在观察性研究或非随机化试验中面临的一个非常大的挑战就是从数据中进行因果推断（Causal Inferences）并估计因果效应（Causal Effects）。在医学研究中，虽然随机对照试验（RCTs）被认为是因果推断的黄金标准，但RCTs用于因果推断并不总是可能的或可行的[1,2]，比如，患者遵循医嘱使用某种药物的行为符合真实世界情况，即医生根据患者的个人信息、既往史、疾病情况以及患者意愿等信息而非随机的分配药物治疗，故不同治疗组患者的基线特征分布显示差异，即存在混杂因素，而关注的结局会受到这些混杂的影响。若此时直接分析治疗对结局的因果效应，则显然是不合理的[3]。即使是在一个RCT可行且被实施的情况下，由于出现的治疗不依从问题破坏了随机化，这也会影响我们关于治疗或处理因素对疗效结局的因果推断[4,5,6]。在所有这些情况下，使用一些统计方法或技术对混杂因素进行统计调整也许可能得出更有效的因果推断，比如，协方差分析法（Analysis of Covariance（ANCOVA）models）[7]，工 具 变 量 法（Instrumental Variable Approaches）[8]以及倾向评分法（Propensity Score Models）[9,10]。

本文介绍的倾向评分（Propensity Score，PS）在概念上是一个简单的统计工具，它允许研究人员通过平衡非随机设计的非等价组来做出更精确的因果推断。简单的说，PS就是给定很多潜在的混杂变量取值，研究个体被分配到处理组而非对照组的概率。以PS为条件，所有观测到的混杂变量与处理分配相互独立，且在大样本的情况下，混杂变量在不同处理组之间的分布几乎相同，且估计的处理变量对结局的因果效应不会受到混杂的影响[11]。Rosenbaum和Rubin以及Stuart提出了利用PS进行分层（stratification）和配比（matching）来分析因果效应[10,12]。Hirano等提出了利用PS进行加权（weighting）来分析因果效应[13]。虽然这些方法已经开始被广泛的使用[10,14,15,16,17]，但是文献中几乎所有的例子都是使用带参数的Logistic回归模型来估计PS，并且假设模型中的混杂变量关于处理变量的对数优势比（Log-odds）是线性的。虽然，通过变量选择技术，比如向前法等，模型也可能挑选出的交互项或非线性项，但更灵活的PS估计方法却很少得到关注。

本文阐述广义Boosted模型(Generalized Boosted Models，GBM))是一种现代多元非参数回归技术，可用于对PS的估计。根据数据变量的类型，GBM利用自适应算法自动的去估计大量混杂变量与处理变量之间的非线性关系，特别是它们之间线性、非线性或交互关系等函数形式无法确定时，此方法很有优势[18]。目前，估计PS的很多统计方法缺乏灵活性，且需要进行混杂变量选择。而变量选择风险会使得因果效应估计有偏，比如，变量选择过程中遗漏对处理分配很重要的混杂变量，或者错误指定了线性、非线性或交互关系。本研究利用GBM倾向评分加权法对来自6省市37家医院集中监测数据进行分析。以使用丹红注射液是否联合其它药物为处理因素，实验室检查指标谷丙转氨酶（ALT）用药前后是否异常变化作为结局，用实例阐述GBM倾向评分加权法的优势及应用过程，以期指导相关医学人员进行他们自己的因果推断研究。

1 资料来源

1.1 数据说明

本研究数据来自6省市37家医院参与研究的医院集中监测平台，监测对象是从2009年4月至2013年8月所有使用丹红注射液的住院患者，共计纳入有效病例数30888例。数据包括患者基本信息、病症情况、给药情况、综合情况、实验室检查指标这五大类信息，共收集1834个变量。其中，患者基本信息包含年龄、性别、体重指数、怀疑过敏物、医院、住院科室等78个变量，病症情况包含适应病症、是否中医辨证等671个变量，给药情况包含是否首次使用丹红注射液、用药次数、合并用药名称等970个变量，综合情况包含病情变化情况、症状改善情况等115个变量，实验室检查指标包含血常规、尿常规、谷丙转氨酶（ALT）、谷草转氨酶（AST）等96个变量。我们提取有ALT检查的患者共5619例，用药前后都有ALT检查的患者共625例。

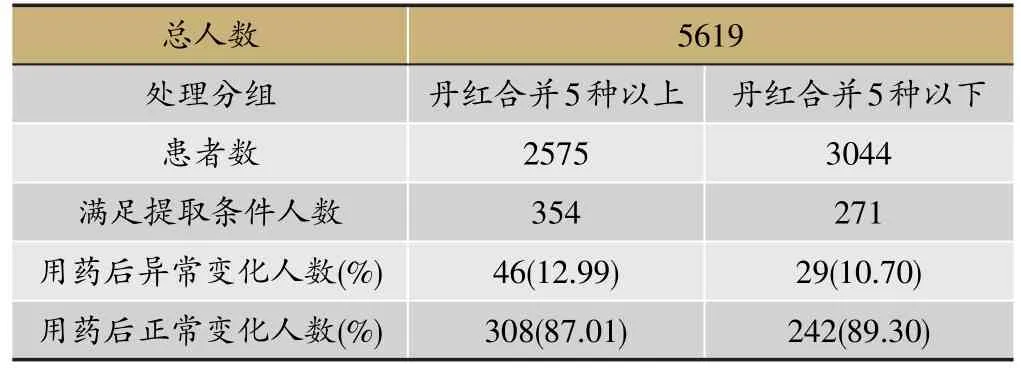
表1 ALT异常值情况

1.2 处理及结局变量说明

本研究需要说明两类人群：（1）在所有使用丹红注射液且合并用5种及以下药物（简称“丹红合并5种以下”）的患者中，记录其用药前后的ALT值变化情况；（2）在所有使用丹红注射液且合并用5种以上药物（简称“丹红合并5种以上”）的患者中，记录其用药前后的ALT值变化情况。我们定义处理变量为“丹红合并5种”，丹红合并5种以上取值1，丹红合并5种以下取值0；安全结局为用药前后ALT值是否有异常变化，异常变化取值1，正常变化取值0。理化指标依各家医院不同范围分别考虑异常值情况。具体分布如下表1。

1.3 混杂因素

通过对混杂因素在两个处理组之间的组间比较、特征选择及临床经验判断，考虑与处理选择和结局都可能相关的混杂因素包括：年龄、性别、体重指数、个人药物食物等过敏史、家族药物过敏史、过敏性疾病史、医院、住院科室、是否辨证、是否首次用丹红、用药次数、最后一次给药间隔、最后一次静滴速度、单次给药量、溶媒种类、病情情况、症状情况、证候判定、体征情况等共87种，它们是与处理变量和ALT异常变化可能有关的所有混杂因素。这些混杂中的多分类变量都经过哑变量编码。

2 数据分析方法

本文利用GBM倾向评分加权法对医院集中监测数据进行分析及因果推断的主要过程分为：定义因果效应、GBM估计倾向评分、倾向评分样本加权、评估混杂因素平衡准则、PS加权估计平均因果效应、敏感性分析。

2.1 定义因果效应

本文在观察性研究或非随机化试验中，定义了一个在接受处理和未接受处理（即对照）之间的因果效应，它主要利用了虚拟事实（counterfactuals）的概念[11,13]。假定研究总体中每个个体都有两个可能的结局值：y1是个体被分配或接受处理条件时的结局值，y0是个体被分配或接受对照条件时的结局值。这两个值对每个个体仅有一个值被观察到，而另一个值是不可能被观察到的。我们称未观察到的那个值为虚拟结局值。令z为处理变量，如果个体接受处理，则z=1,否则z=0，从而被观察的结局值y=zy1+(1-z)y0。总体人群的平均因果效应（Average Treatment Effect，ATE）定义为 E(y1)-E(y0)，记为 ATE[19]，即

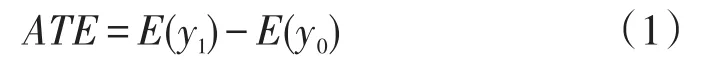
比如，在所有使用丹红注射液的患者中，合并用其它药物的处理相对于未合并用其它药物的对照对结局变量影响的平均因果效应，即理想上所有使用丹红注射液的患者，如果他们都合并用其它药物与他们如果都未合并用其它药物相比较，我们期望观察到两组患者在ALT指标异常变化的差异。

然而，通常我们只对对象接受某种处理的事实与他们未接受此处理的虚拟进行比较的因果效应感兴趣，即处理组平均因果效应（Average Treatment effect among the Treated，ATT），记为 ATT[19]。定义 E(y1|z=1)为处理组个体接受处理条件后的平均结局值，E(y0|z=1)为处理组个体接受对照条件后的平均结局值。那么，处理组平均因果效应

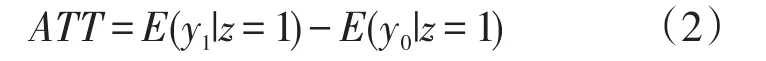
比如，在所有使用丹红注射液且合并用其它药物的患者中，处理的事实与虚拟之间的平均因果效应，即理想上所有使用丹红注射液且合并用其它药物的患者与他们如果都未合并用其它药物相比较，我们期望观察到两组患者在ALT指标异常变化的差异。

根据不同因果效应的定义，大多数医学研究中要求研究人员都需要确定一个确切的因果问题，通常他们会对ATT的估计更感兴趣，因为它包含了更多的暴露于某种风险的个体信息。本研究的数据分析主要是估计ATT。

2.2 GBM估计倾向评分

对每个接受处理的个体而言，E(y0|z=1)中的结局值y0是无法观测到的，可利用对照组数据进行估计。然而，当多个混杂变量在处理组和对照组之间存在差异时，此估计值是有偏的，从而ATT的估计也会有偏。利用PS平衡组间差异、调节估计偏倚成为必要的分析手段[11]。在给定一组观察到的混杂变量条件下，PS是指总体中个体接受处理而不是对照条件的概率，记为e(X)=P(z=1|X)。假定X表示一组可观测到的基线混杂变量的向量，则倾向评分e(X)是关于向量X的函数。给定e(X)的条件下所有观察到的混杂变量分布在处理组与对照组之间几乎匹配或相同，即处理分配变量接近随机分配设计（random assignment designs）的效果[11]。换句话说，给定e(X)的条件下，对照组中可观测到的y0分布等于处理组中无法观测到的y0分布，从而，可以利用对照组观测到的y0的数据来估计E(y0|z=1,e(x))，且估计得到的ATT为处理组平均因果效应的无偏估计[11]。在此之前，关键是要正确或精准的估计倾向评分e(X)，那么在具体实现GBM估计e(X)的过程中，必须明确两个重要问题：

（1）估计e(X)的模型选择及函数形式的确定

目前，估计PS的方法大多数是利用参数线性Logistic或Probit回归建立基线混杂因素对处理变量的函数关系而得出的，但此函数关系必须正确。那么，模型建立过程中就会涉及变量主效应、变量间交互项或变量多项式项的选择[14,15,16,17]，即都是从变量选择开始。比如，可利用变量主效应拟合一个回归模型，然后估计倾向评分对数据进行分层，在每层中对处理组和对照组的混杂变量的均值和标准差进行组间显著性检验（这里可以考虑不同的显著性水平p＜0.05或p＜0.1或 p＜0.2）。若某些混杂变量组间差异统计显著，则模型再考虑它们的交互项或更高阶的多项式项。此过程一直继续到没有显著差异出现为止。但随着大量混杂变量的增加，这些传统的回归方法和变量选择策略可能就不实用了，比如很可能会遗漏重要的混杂变量或者错误指定函数关系。而GBM算法是基于广义增强回归的一个现代的非参数Boosting方法，它能提供一个灵活的、强大的且自动的数据自适应算法，可用于估计处理变量和大量混杂变量之间的非线性关系以及大量混杂变量多阶交互项的关系，即使是这些混杂变量中大多数是彼此相关的或它们与处理变量不相关的情况。另外，从预测误差方面来看，Boosting方法优于其它的方法[20,21]。许多Boosting算法的变种已经出现在机器学习和统计计算文献中，比如AdaBoost算法[22]，Gradient Boosting machine 算法[20]，GBMs算法[23]以及LogitBoost算法[24]等。特别是当模型中存在大量混杂变量，且它们与处理选择之间线性、非线性或交互效应等函数形式无法确定以及在没有太大降低估计精度的情况下，此方法用于构建大量混杂变量的倾向评分模型的优势更明显[25]。

（2）估计PS模型中的混杂变量选择。

一般来说，GBM估计e(X)的模型中应尽可能地选择所有即与处理变量相关又与结局相关的基线混杂变量，也可以考虑其它策略，比如只包括和处理变量有关的基线混杂变量等[9,26]）。通常，需要纳入分析的混杂变量个数以及估计倾向评分的模型都是未知的，所以倾向评分的估计需要进行混杂变量选择和函数形式的确定。一般的变量选择都是根据统计显著性或降低预测误差的准则在模型中进行变量选择或变量函数形式的确定。但倾向评分模型中混杂变量选择的一个关键准则是基于倾向评分的条件下，如何使处理组与对照组的混杂变量分布几乎匹配或相似。

2.3 倾向评分样本加权

本文研究主要利用GBM估计倾向评分，然后再给对照组的个体进行逆概率加权，使得对照组个体特征变量的分布与处理组个体特征变量的分布平衡[14,18,19,,27]。令 f(X|z=1)表示处理组个体的混杂变量分布，f(X|z=0)表示对照组个体的混杂变量分布。如果处理是被随机分配的，则希望这两个分布是一样的。而实际上，它们是不同的，所以需要构造一个权重w(X)，使得

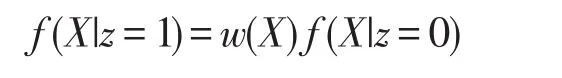
其中w(X)=e(X)/[1-e(X)]。很显然，如果对照组个体i具有与处理组个体相似的混杂变量，则被分配到处理组的概率更大，即个体i将有更大的e(X)，从而就有更大的权重w(X)，反之亦然。例如，如果处理组和对照组中65岁女性的比例分布分别为10%和5%，那么自然希望附权重2（=0.1/0.05）到对照组中每个65岁女性个体上，使得他们和处理组具有相同特征个体一样的比例分布。GBM倾向评分加权法就是基于广义增强回归（Generalized boosted regression）模型来估计倾向评分并进行逆概率加权的方法。

2.4 评估混杂因素平衡准则

使用倾向评分进行调整以后的数据在混杂因素上的组间平衡需要得到评估，GBM算法是以处理组和对照组之间混杂变量特征达到平衡为准则，它不对两组混杂变量的均值和标准差（means and standard deviations）进行组间显著性检验，而是利用常用的测量平衡或匹配的最佳工具：平均标准绝对均值差（Average Standardized Absolute Mean difference，ASAM）和 K-S统 计 量（Kolmogorov-Smirnov test statistic）[10]。比如，当ASAM小于0.2时或K-S统计量达到最小时，就认为混杂因素在组间达到平衡。由于计算ASAM的过程要用到每个混杂变量在处理组的标准差，而当数据存在缺失或标准差为0的情况时，ASAM无法计算，所以本研究采用K-S统计量作为测量两组混杂变量平衡的工具。K-S统计量在GBM算法过程是逐渐减小的，当达到某个最小值开始，随后K-S统计量会逐渐增大。这里不能确保算法对K-S统计量会有全局的最小值，若K-S统计量无法达到最小，则调整参数或考虑其他的估计方法是必要的。

2.5 PS加权估计平均因果效应

当我们估计平均因果效应的时候，倾向评分可以被用来对观察值进行加权处理[13]。为了估计ATT，关键就是估计E(y0|z=1)，在此先给对照组样本中的每个个体i(i=1,2,…,N)加权wi=e(Xi)/[1-e(Xi)]，它表示具有特征向量X的个体i可能被随机选择分配到处理组的优势比。如果个体i是在处理组，则它被观测到的结局值为yi=y1i；如果个体i处在对照组，则它被观测到的结局值为yi=y0i。如果我们假设给定X的条件下处理变量z与结局值yi是独立的，即

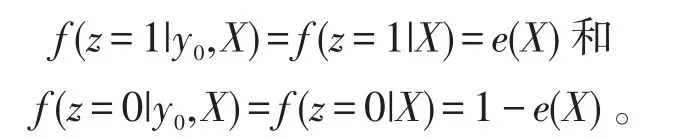
那么，我们可以给出E(y0|z=1)的估计为：

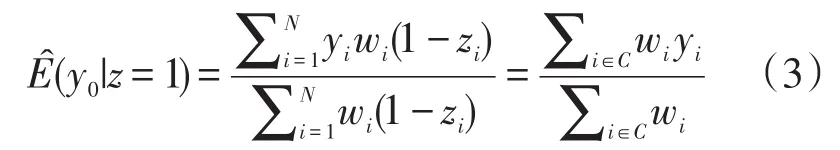
这里i∈C表示对照组中第i个观测个体。等式（3）可以用来估计处理组个体接受对照条件后的平均结局值[7]。令NT和i∈T分别表示处理组中样本量及第i个观测个体，则

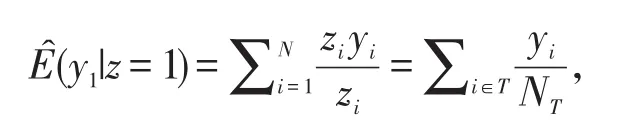
可以用来估计处理组个体接受处理条件后的平均结局值[7]。从而，处理组平均因果效应 ATT的估计为在大样本且给定几个假设条件的情况下，加权的因果效应估计几乎是无偏的。其中，最重要的假设就是观测到的混杂变量可以解释处理组与对照组之间所有事先存在的差异，而这些差异会影响分析的结局。此外，还要求个体的结局不受其他个体的处理变量以及其它与处理无关的因素的影响。本研究建立结局变量的对数似然比相对于处理变量的Logistic回归模型，则处理变量的回归系数值可作为处理组平均因果效应的估计值。

2.6 对潜在混杂识别的敏感性分析

通常，我们只对观察到的变量构建估计倾向评分的模型，模型中不包含未观察到的混杂因素即潜在偏倚，我们需要对是否可能存在潜在的混杂进行识别，即所谓的敏感性分析。潜在偏倚的存在会导致混杂变量观察值相同的个体其接受处理的概率不同，即处理分配依赖于未观察到的混杂变量。例如，混杂变量观察值相同的研究个体，当存在一些未观察到的潜在混杂变量，即这些潜在变量分布存在差异，则研究个体被分配到处理组的概率也不同。从而，对权重和平均因果效应的估计会产生误差。由于无法从数据中估计出潜在偏倚，故只能通过检验或评估研究结果对潜在偏倚的敏感程度来识别是否还存在其它的潜在变量，即对潜在混杂识别的敏感性分析[9,18]。

若研究中确实存在潜在偏倚，研究个体被分配到处理组的真实优势比(即真实权重)就不是wi=w(Xi)，而是wi=w(Xi,Hi)，这里H表示无法观测到的潜在混杂。为了检验ATT对潜在混杂的敏感性，我们需要识别随着倾向评分权重wi的变化，变化的敏感性。通常的做法是从倾向评分模型中移除一个观测混杂变量，把它当成H，对倾向评分重新估计，得到的新的权重为w(Xi)，而原始的权重为w(Xi,H)。通过从倾向评分模型中依次移除一个混杂变量，我们可以检验ATT对潜在偏倚是否敏感[18]。

3 分析结果

本文利用GBM估计倾向评分，通过使K-S统计量达到最小，不断加权调整模型，很好的平衡了丹红合并5种以下和加权的丹红合并5种以上的混杂因素。理论上，很大的迭代次数能使K-S统计量达到最小，但迭代次数越多，模型估计的时间越长。实际应用中选择较大的迭代次数，若K-S统计量无法达到最小，再加大迭代次数，或考虑其他的估计方法。本研究设定迭代次数为20000。另外，取一个折中的4阶交互项可确保模型形式的正确识别和模型的精确估计，即在估计倾向评分的模型中自动考虑混杂变量之间的四阶交互项。一般来说，若要考虑5阶或更高阶的交互项，则要求研究样本足够的大。此外，模型中设定一个足够小的收缩系数用于排除模型中大多数不相关的混杂变量，产生一个仅体现最重要作用的混杂变量和交互项的稀疏模型[24,28]。本研究取一个非常小的数值0.0005。再有，利用leave-one-out刀切法(jackknife)来估计因果效应的标准差。本研究的全部算法都可基于R统计软件中的gbm、survey和Twang等包[29]编程实现。

3.1 GBM估计的倾向评分和权重

根据上面讨论的过程，K-S统计量达到最小值的迭代次数为5217次。根据观察到的87个混杂变量对模型对数似然度整体改善的贡献，算法自动测量并排序每个混杂变量对处理变量的重要程度。模型似然度的大约67%的增加是由于4个混杂变量导致的：医院代码(22.48%)、用药次数分组(21.81%)、住院科室(16.14%)和单次给药量(7.37%)。这四个混杂变量似乎都与处理变量丹红合并用药种类数有关。对每个变量的边际分布，可利用偏依赖图(Partial dependence plots)[20]来查看。边际分布图显示：当对其它86个混杂变量分布边际积分以后，患者被分配到丹红合并5种以上的对数优势比与每个混杂变量之间的关系为非线性的（参见图1）。从图1看出，比如，住在内分泌科或肾脏病科或心血管内科患者更有可能被分配到丹红合并5种以上组，这种非线性体现了GBM方法的优势。如果能够根据专业知识认为其中一些混杂变量和处理变量没有太大相关性，则可以考虑排除少量的混杂变量，最终接受包含更小混杂变量集的倾向评分模型。根据本数据分析的经验，我们从模型中删除少量不重要的混杂变量之后，倾向评分模型估计的结果几乎没有变化。

图2中左图显示了“丹红合并5种以上”和“丹红合并5种以下”的倾向评分的分布，大多数个体的权重集中在0～0.5之间，少数个体的权重超过1.5达到2。两组的倾向评分重叠范围很小。理想上，我们希望看到两组的倾向评分之间有更大的重叠，因为小的重叠范围会使因果效应的估计有更大的方差，从而出现倾向评分加权后对照组与处理组的混杂变量分布不能很好匹配的危险。然而，GBM模型中非线性关系暗示着在倾向评分之间的差异并不等于两组混杂变量均值之间的差异。McCaffrey等和Ridgeway用实例说明即使两组倾向评分的分布几乎相同，也并不能给两组混杂变量均值带来更好的平衡，反之，用不同的迭代次数，即使GBM估计的倾向评分和权重迥然不同，但也能在两组混杂变量分布上产生很好的平衡[18,30]。

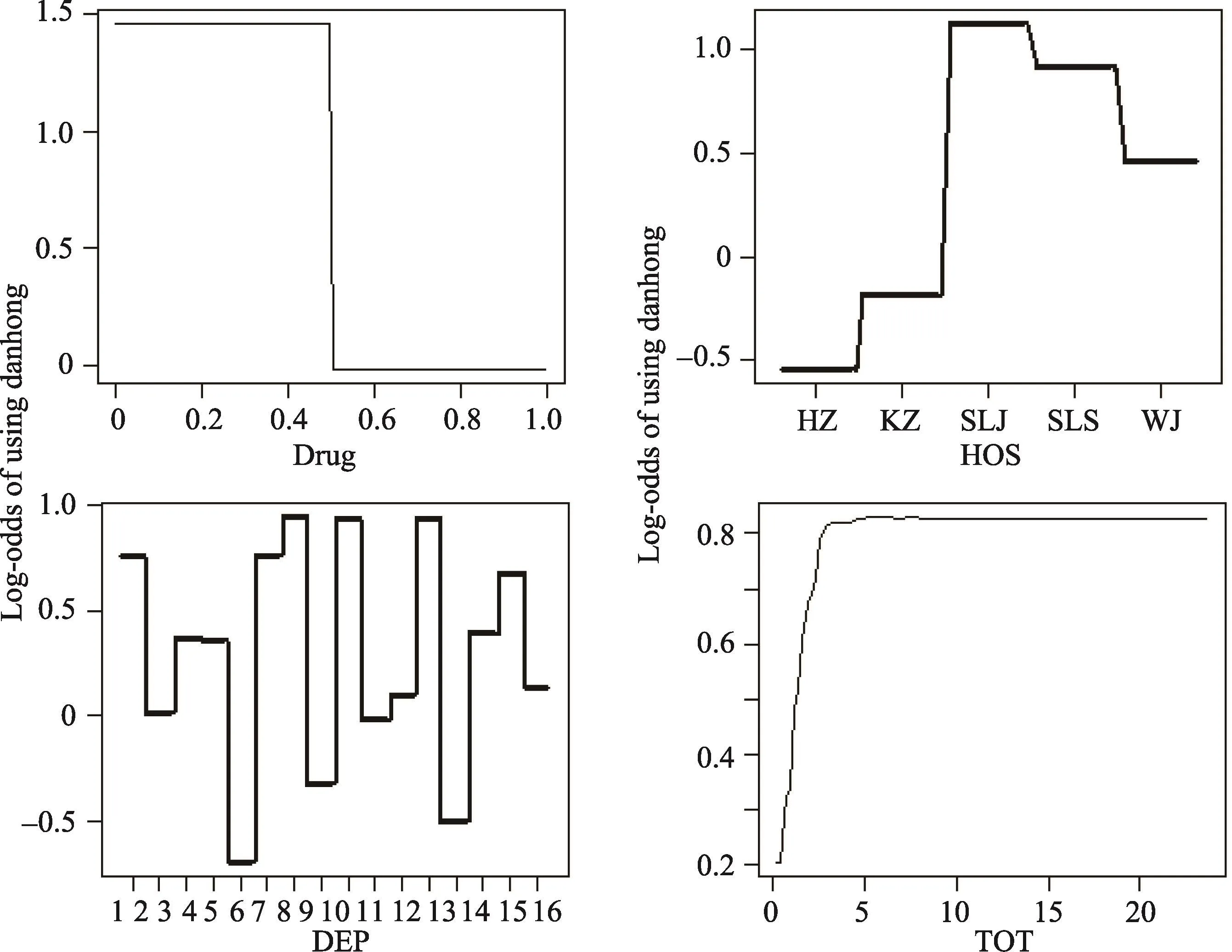
图1 四个混杂变量偏依赖图（Partial dependence plots）。Drug表示用药次数分组，HOS表示医院代码，DEP表示住院科室

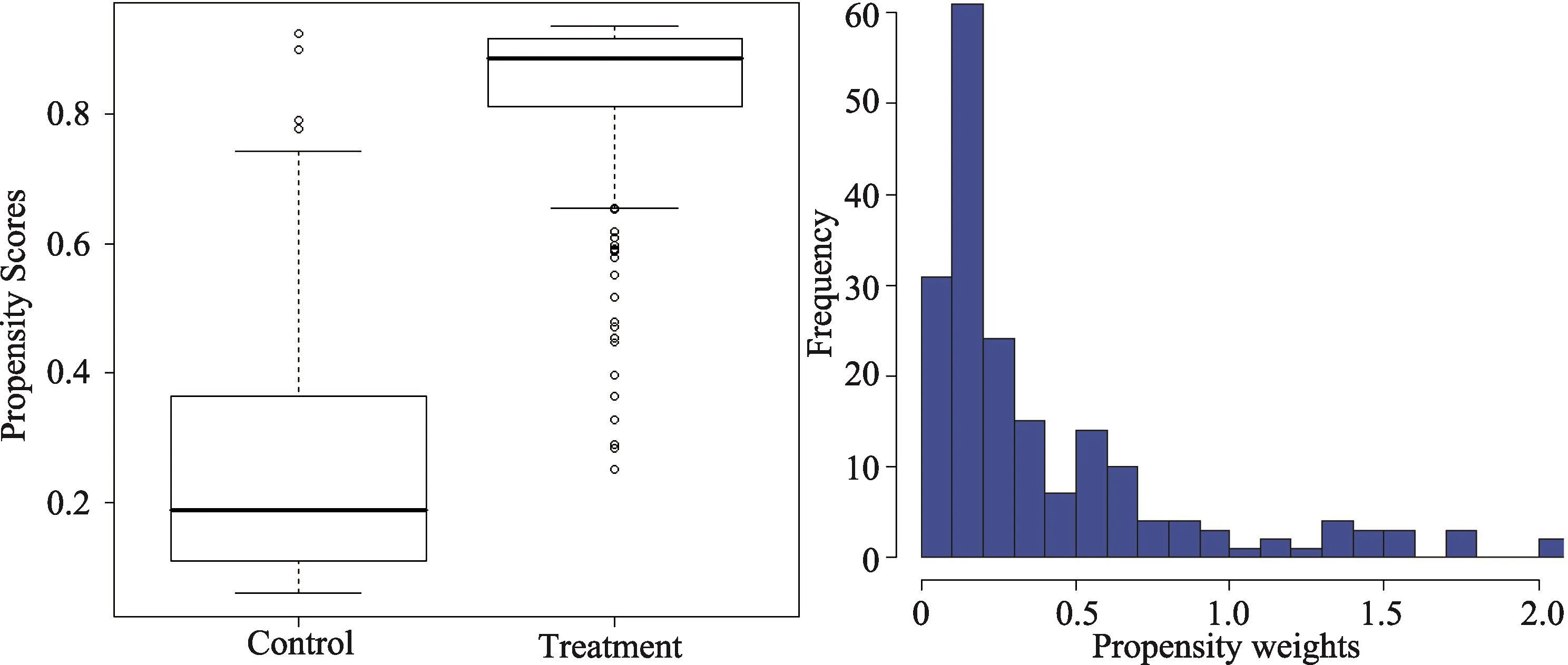
图2 左图为“丹红合并5种以上（Treatment）”和“丹红合并5种以下（Control）”患者的倾向评分分布箱线图。右图为权重在“丹红合并5种以下”患者中的分布直方图

3.2 混杂变量的平衡准则

混杂变量之间的均值差在利用PS给对照组个体进行加权之前是可以直接被观察到的。表2给出了“丹红合并5种以上”和“丹红合并5种以下”两组部分基线混杂变量在倾向评分加权前后的分布特征及K-S统计量、检验p值。

我们可以发现：在“丹红合并5种以上”患者人群中，医院代码为SLJ，住院科室为心血管内科等变量的比例要明显更高；年龄、住院天数的平均值稍微更低。纵观模型中所有87个混杂变量，未加权的K-S统计量有十几个混杂变量的K-S统计量大于0.2。两组混杂变量之间的差异在利用PS给对照组个体进行加权之后被大大的减小了。K-S统计量平均值由0.12减小到0.06，减小了50%。实际上，模型中共有87个变量，我们只在表2中列出影响模型似然度变化比较大且两组间差异明显的前25种混杂变量的情况。

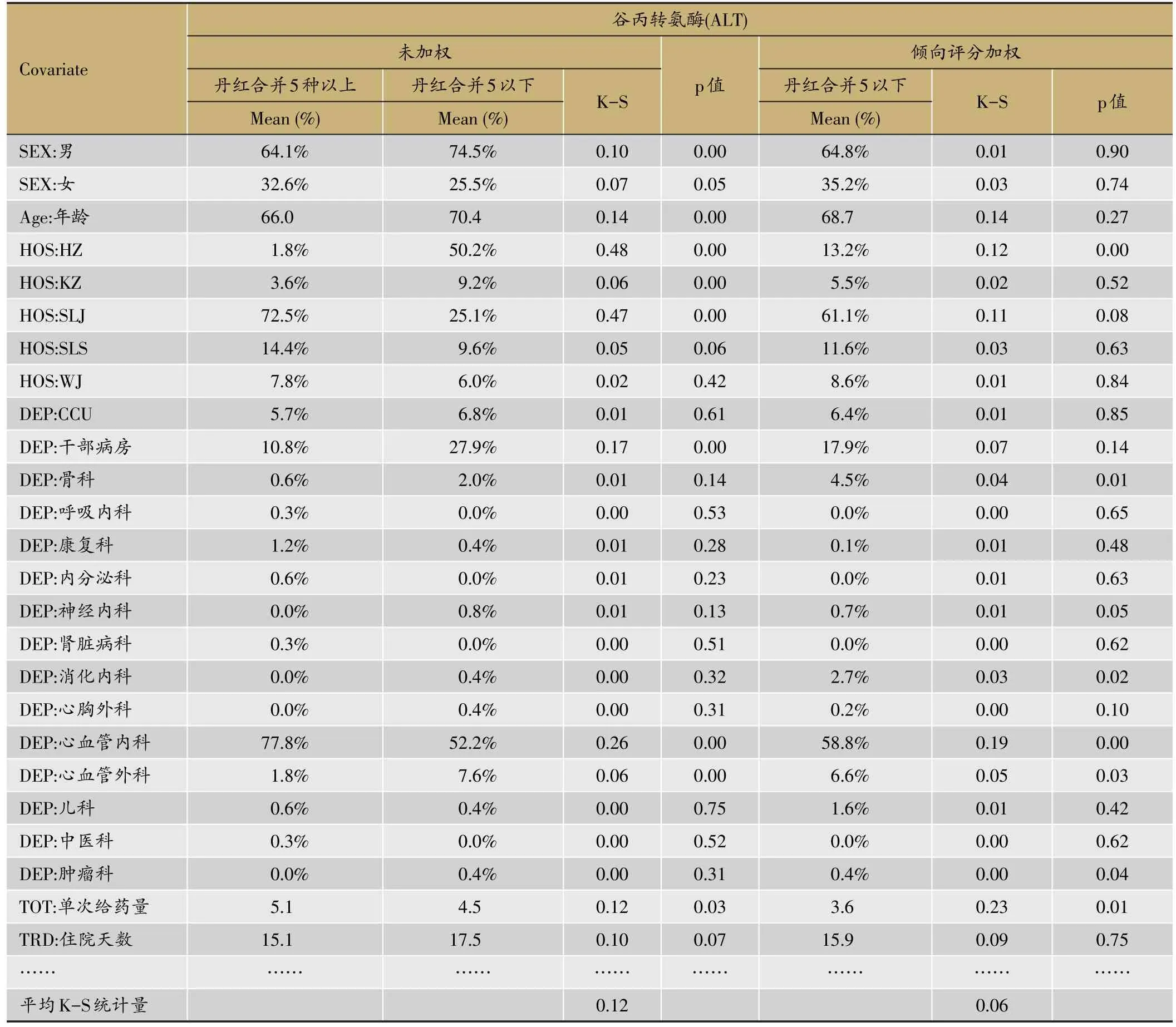
表2 两组部分基线混杂变量在倾向评分加权前后的分布特征及K-S统计量、检验p值

图3是加权前后的p值与均匀分布值的比较图，经过倾向评分加权后，87个基线混杂变量在两组之间的差异接近于随机分配的结果，即患者被随机分配到“丹红合并5种以上”和“丹红合并5种以下”组。两组之间混杂变量的K-S分布无差异独立性检验值服从[0,1]均匀分布，值是对混杂变量的组间检验值，连续变量则为t检验值，分类变量则为卡方检验值。许多混杂变量（红色实圆）加权前在两组间有显著的差异，故拒绝原假设，即许多值接近于0。大多数混杂变量（空心圆）加权后在两组间的差异不显著，故值都沿着[0,1]均匀变量的累积分布45度的直线分散开，即p值服从[0,1]均匀分布一样。

3.3 结局分析结果

构建ALT指标异常变化的对数似然比与处理变量“丹红合并5种”之间的Logistic回归模型，则模型中变量“丹红合并5种”前的回归系数值可作为处理组平均因果效应的估计值。下面表3的头两行表示不同方法估计得到的及检验 p值。未加权logistic回归分析表明“丹红合并5种以上”导致ALT发生异常变化的对数优势比大于0(0.016），估计的因果效应不具有统计显著性(p值=0.498＞0.05）；但经过GBM倾向评分加权后，logistic回归分析表明“丹红合并5种以上”导致ALT发生异常变化的对数优势比大于0(0.047），估计的因果效应具有统计显著性(p值=0.048＜0.05）。

利用PS加权和少数未平衡的混杂变量加入模型中进行调节相结合的方法来估计因果效应，可获得双稳健（doubly robust）的因果效应估计[9,31,32]。如果倾向评分估计正确或回归模型指定正确，则它们的估计是一致的。例如，在对ALT指标分析时，注意到加权后，虽然使得住院科室混杂变量分布在两组间更接近，但还是存在很明显的分布差异，如住在心血管内科患者中“丹红合并5种以上”组占77.8%的患者，而“丹红合并5种以下”组只占58.8%。所以，这时候把“住院科室”等混杂变量加入到倾向评分加权后的logistic回归模型，可以适当调节还存在的混杂偏倚，估计更稳健的因果效应。从表3的最后一列可以看到，混杂变量调节后的因果效应又减小到0.036，且依然不具有统计显著性(p值=0.091＞0.05）。说明这里对ALT的分析结论需要谨慎对待。

一般来说，倾向评分模型以及回归模型形式对估计因果效应很敏感，但对很强的因果效应，其估计的结果应该是一致的。本研究中Logistics回归模型对ALT指标的分析出现不一致的情况，表明“丹红合并5种以上”对ALT异常变化的因果效应并不是很强。

McCaffrey还用实例说明GBM模型对e(X)估计的预测误差更小，即GBM提供更精确的倾向评分e(X)的估计；同时也能很好的平衡两组混杂变量均值；因果效应的估计值更小且具有更小的标准误差[18]。

3.4 敏感性分析结果

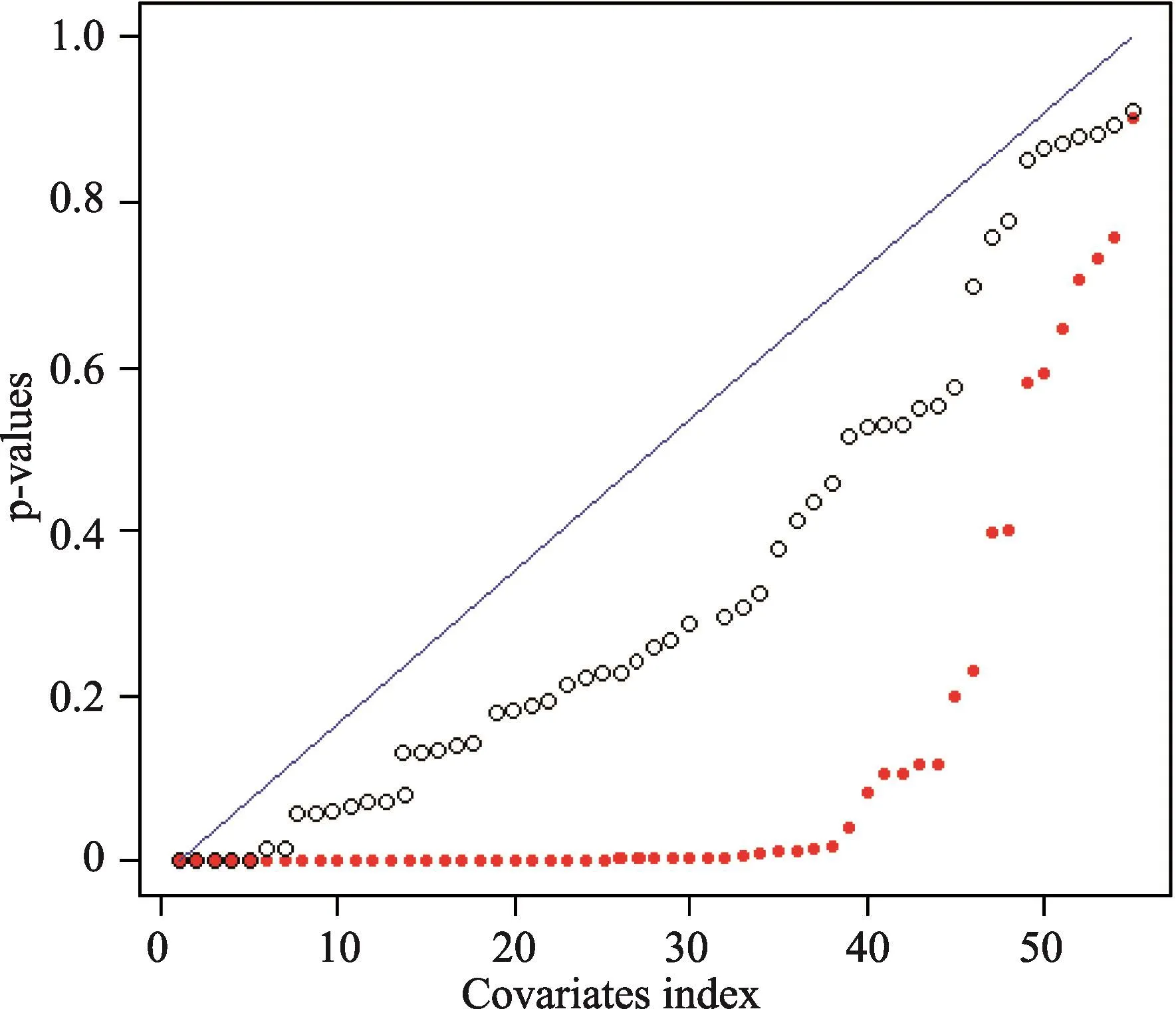
图3 加权前后两组87个混杂变量差异检验的p值与均匀分布值的比较图

由于PS估计的模型中涉及观察到的变量太多，在不影响分析结果示范解释的情况下，表4只列出前几行敏感性分析结果。第一列字母Var表示从估计倾向评分模型中移除的观察到的混杂变量；第二列E0表示排除Var后由倾向评分模型估计的E(y0|z=1)，即等式（15）的值；第三列range(ai)表示排除Var中对应变量后得到的一组ai值的范围（最小值和最大值）；第四列obseved(ρ)表示第三列的ai值与结局yi计算的相关系数cor(ai,yi)=ρ；第五列range(ρ)表示从第三列ai值的经验分布中找到的尽可能最大的和最小的ρ；第六列range(E0)表示使得ρ尽可能最大和最小的多组ai值，代入等式（15），估计得到E(y0|z=1)的最大值和最小值。第7列为 break even(ρ)。

表4的结果表明，有些混杂变量的range(E0)与E0比较，变化都不大，且它们对应的break even(ρ)都很小，则说明ATE1对潜在偏倚不敏感，即表4暗示着本研究可能不存在未观察到的潜在混杂。

表3 用未加权Logistic回归、GBM倾向评分加权和双稳健法对因果效应的估计

表4 丹红合并5种的估计因果效应的敏感性分析

4 结论与讨论

对观察性研究或非随机化设计的资料或存在混杂因素的研究资料进行因果推断，目前比较成熟的统计方法就是倾向评分法。考虑到大量混杂因素的存在，GBM估计倾向评分的方法非常具有吸引力，它提供一种自适应估计倾向评分算法，可分析包含多个混杂变量和多种类型变量(连续的、名义的或有序的)的数据。由于GBM是一种非参数的估计方法，则可以避免模型被错误指定而导致因果效应估计有偏，且当处理变量和大量混杂变量之间的非线性关系，特别是当模型中混杂变量与处理变量之间的函数形式无法确定时，此方法的优势凸显。

本文医学实例数据中包含大量的临床信息且它们和丹红合并5种的关系存在非线性的情况(如图1)。虽然丹红合并5种以下和丹红合并5种以上的多数基线混杂变量在加权前存在较大差异，但经过加权平衡以后，PS估计模型中所有混杂变量组间均值差异几乎达到平衡（如表2），若不消除这些混杂变量的组间差异，则会影响对因果效应的估计。GBM提供更精确的倾向评分的估计对两组混杂变量均值平衡的更好，且加权估计并没有太大的提高因果效应估计的标准误。GBM提供更精确的倾向评分e(X)的估计对两组混杂变量均值平衡的更好，且加权估计并没有太大的提高因果效应估计的标准误。考虑到模型的复杂度，如果存在一些混杂变量对模型似然度的改善很小且它们在两组的差异也几乎很小，特别是如果能够根据专业知识认为其中一些混杂变量和处理变量没有太大相关性，则可以考虑排除这些混杂变量，最终只接受包括更小混杂变量集的倾向评分模型。

虽然，GBM相比于其他模型有很多的优势，但研究人员在利用GBM倾向评分加权法的过程中必须适当的调整估计PS的模型和估计因果效应的模型。（1）在估计PS的模型过程中，通过变量选择的统计原则和临床经验，纳入分析的混杂变量；灵活确定估计倾向评分的模型函数形式确定，设置模型为4阶的最高阶交互项；再有，足够大的迭代次数(本研究为20000)和足够小的收缩系数(本研究为0.0005)能够提供更好的模型，但是却大大增加了迭代计算的复杂度，且同时减小混杂变量对模型的边际改善，可能导致算法不收敛。因此，给定一个合适的交互项阶数以及一个足够小的收缩系数，GBM很自然的成为一个估计倾向评分的有效工具。（2）GBM倾向评分对数据加权后，并不能完全平衡数据中每个混杂变量在两组间的差异。虽然存在的差异并不大，且混杂变量在两组的分布基本接近，但最好利用倾向评分加权结合线性回归调节的方法对估计因果效应再进行估计，在加权后数据上构建的Logistics回归模型中加入适当的混杂变量，可获得双稳健的因果效应估计。当研究的处理对结局存在很强的因果效应时，则模型中对因果推断的结果保持一致。本研究中对ALT的分析结果出现不一致的情况，说明本研究中“丹红合并5种以上”对ALT异常变化的因果效应并不是很强。

本研究利用GBM倾向评分加权法，对一组观察性医学数据按照以下过程：定义因果效应、估计倾向评分、倾向评分样本加权、评估混杂因素平衡准则、PS加权的Logistics回归估计平均因果效应、对潜在混杂识别的敏感性分析，进行了分析，以期指导相关医学人员根据各自的研究项目进行相关的因果推断研究。

1 Mccall,R B,Green B.Social Policy Report,XVIII.2004.Beyond the methodological gold standards of behavioral research:Considerationsfor practiceand policy.

2 West SG..Alternatives to randomized experiments.Current Directions in Psychological Science,2009,18(5):299-304.

3 杨伟,易丹辉,谢雁鸣,等.基于GBM倾向评分法对疏血通注射液导致谷丙转氨酶异常变化的影响分析.中国中药杂志,2013,(18):3039-3047.

4 Mercer S L,Devinney B J,Fine L J,et al.Study designs for effectiveness and translation research:Identifying trade-offs.American Journal of Preventative Medicine,2007,33(2):139-154.

5 Sanson-Fisher R W,Bonevski B,Green L W,et al.Limitations of the randomized controlled trial in evaluating population-based health interventions.American Journal of Preventative Medicine,2007,33(2):155-161.

6 Stuart E A,Perry D F,Le H N,Ialongo NS.Estimating intervention effects of prevention programs:Accounting for noncompliance.Prevention Science,2008,9:288-298.

7 Shadish W R.,Cook T D.,Campbell D T.(2002).Experimental and quasi-experimental designs for generalized causal inference.Boston:Houghton-Mifflin.

8 Harder V S.,Stuart E A,Anthony J.Propensity Score Techniques and the Assessment of Measured Covariate Balance to Test Causal Associations in Psychological Research.Psychological Methods,2010,15(3):234-249.

9 Rosenbaum,P.(2002).Observational studies(2nd).New York:Springer-Verlag.

10 Stuart EA.Matching Methods for Causal Inference:A review and a look forward.Statistical Science,2010,25(1):1-21.

11 Rosenbaum PR.,Rubin D B.The central role of the propensity score in observational studiesfor causal effects.Biometrika,1983,70(1):41-55.

12 Rosenbaum P R.,Rubin D B.Reducing bias in observational studies using sub-classification on the propensity score.J Am Stat Assoc,1984,79:516-524.

13 Hirano K.,Imbens G.,Ridder G..Efficient estimation of average treatment effects using the estimated propensity score.Econometrica,2003,71:1161-1189.

14 Hirano K.,Imbens G.Estimation of causal effects using propensity score weighting:An application to data on right heart catheterization.Health Servicesand Outcomes Research Methodology,2001,2:259-278.

15 Mojtabai R.,Graff Zivin J.Effectiveness and cost-effectiveness of four treatment modalities for substance disorders:A propensity score analysis.Health Serv Res,2003,38:233-259.

16 Harder V.S.,Stuart E.A.,Anthony J.Adolescent can nabisproblemsand young adult depression:Male-female stratified propensity score analyses.Am JEpidemiol,2008,168:592-601.

17 Slade E P,Stuart E A,Salkever D S,et al.Impacts of age of onset of substance used is orders on risk of adult incarceration among disadvantage Durban youth:A propensity score matching approach.Drug Alcohol Depen,2008,95:1-13.

18 McCaffrey D F,Ridgeway G,Morral A R.Propensity Score Estimation With Boosted Regression for Evaluating Causal Effects in Observational Studies.Psychological Methods,2004,9(4):403-425.

19 Wooldridge J.(2001).Econometric analysis of cross section and panel data.Cambridge:MITPress.

20 Friedman J H.Greedy function approximation:A gradient Boosting machine.Ann Stat,2001,29:1189-1232.

21 Madigan D,Ridgeway G.Discussion of Least angle regression by Efron.Ann Stat,2004,32:465-469.

22 Freund Y,Schapire R.A decision-theoretic generalization of on-line learning and an application to boosting.J Comput Sys Sc Int,1997,55:119-139.

23 Ridgeway G.The state of boosting.Computing Science and Statistics,1999,31:172-181.

24 Friedman J H,Hastie T,Tibshirani R.Additive logistic regression:A statistical view of Boosting.Ann of Stat,2000,28:337-374.

25 Buhlmann P,Yu B.Boosting with the L2 loss:Regression and classification.JAm Stat Assoc,2003,98:324-339.

26 West SG.,Biesanz JC,Pitts SC.Causal inference and generalization in field settings experimental and quasi-experimental designs.In H.T.Reis&C.M.Judd(Eds.),Handbook of research methods in social and personality psychology,2000:40-88.New York:Cambridge University Press.

27 Rosenbaum P R,Rubin D B.Constructing a control group using multivariate matched sampling methods that incorporate the propensity score.Am Stat,1985,39:33-38.

28 Tibshirani R.Regression shrinkage and selection via the lasso.J Roy Stat Soc,Series B,1996,58(1):267-288.

29 Ridgeway G.,Mccaffrey D,Morral A.(2010).Toolkit for Weighting and Analysis of Nonequivalent Groups:A tutorial for the twang package.Packagemanual.

30 Ridgeway G.Assessing the effect of race bias in post-traffic stop outcomes using propensity scores.Journal of Quantitative Criminology,2006,22(1):1-29.

31 Huppler-Hullsiek K.,Louis T.A.Propensity score modeling strategies for thecausal analysisof observational data.Biostatistics,2002,2:1-15.32 Bang H.,Robins J.Doubly robust estimation in missing data and causal inferencemodels.Biometrics,2005,61:692-972.

GBM Propensity Score Weighting for Causal Inference Research

Yang Wei1,2,Tang Jinfa3,Yi Danhui4,Li Xuelin3,Li Weixia3,Zhou Xiaohua5
(1.Instituteof Basic Research in Clinical Medicine China Academy of Chinese Medical Sciences,Beijing 100700,China;2.Collegeof Science,Minzu University of China,Beijing 100081,China;3.The First Affiliated Hospital of Henan University of TCM,Zhengzhou 450000,China;4.Center for Applied Statisticsof Renmin University of China,Beijing 100872,China;
5.Beijing International Center for Mathematical Research,Peking University,Beijing 100871,China)

ObjectiveIn observational studies or non-randomized design,the researchers'ability to make causal inferences from data was hampered by confounding factors.This study used this method to analyze a group of observational medical data in order to instruct relevant medical personnel to carry out their own causal inference studies.MethodsAt present,the four main types of propensity scoring methods:matching,stratification,inverse probability weighting and covariate adjustment have been widely used in the study of causal inference.Propensity score method can theoretically eliminate the bias of the observable confounding factors,so that the treatments variables are close to the result of random assignment design,thus,it is estimated that the treatment factor has a causal effect on the outcome.ResultsConsidering the advantages of the inverse probability weighting method over other methods,this paper summarizes the applicable conditions for the estimate of causal effect,particularly illustrates the use of a modern nonparametric statistical technology--Generalized Boosted Models(GBM)and its advantages and disadvantages.ConclusionWhen there is a lot of different types of confounding factors,and uncertain functional forms for their associations with treatment selection in linear,non-linear or interaction effect,and other issues,GBM propensity score weightingmethod can overcomethe obstaclesin theprocessof accurately estimatingpropensity score.

GBM,Propensity Score Weighting,Causal Inference,Observational Studies,Non-randomized Design

10.11842/wst.2017.09.009

R33

A

2017-08-11

修回日期：2017-09-12

＊ 国家自然科学基金委青年科学基金项目（81502898）：大型观察性医学数据的因果图模型研究，负责人：杨伟；重大新药创制专项子课题（2015ZX09501004-001-007）：临床需长期使用的中药口服制剂安全性监测研穷，负责人：李学林。

＊＊ 通讯作者：易丹辉，教授，博士生导师，主要研究方向：风险管理与保险、预测与决策；李学林，主任药师，博士生导师，主要研究方向：中药上市后再评价和中药的应用形式研究

＊＊＊ 混杂因素也称为混杂变量，这两种说法本文会交替使用。

（责任编辑：张娜娜，责任译审：王 晶）