运用Cox模型时打结数据的处理方法探讨＊

张文丽，张 彤，易丹辉＊＊，杨宇飞＊＊

（1.中国人民大学应用统计科学研究中心，北京 100872；2.中国人民大学统计学院 北京 100872；3.中国中医科学院西苑医院 北京 100091）

运用Cox模型时打结数据的处理方法探讨＊

张文丽1,2，张 彤3，易丹辉1,2＊＊，杨宇飞3＊＊

（1.中国人民大学应用统计科学研究中心，北京 100872；2.中国人民大学统计学院 北京 100872；3.中国中医科学院西苑医院 北京 100091）

Cox回归模型是目前生存分析中最为广泛使用的方法之一，模型的假设之一是失效时间不存在打结情况，即个体之间有着不同的失效时间。在实际应用当中，生存时间数据存在打结是很常见的。目前有四种常见的处理方法：Exact法，discrete model法，Efron法以及Breslow法。本文研究目的是比较这四种处理方法的优劣。本文采用模拟进行比较，设置了不同的样本量和打结程度，比较四种方法在拟合统计量，计算时间，参数估计精确性等方面的表现，发现Exact法和discrete model拟合统计量结果最好，但计算耗时最久；Efron法以及Breslow法运算较快但是在参数估计方面存在偏差。另外，样本量和打结程度也影响处理的结果，总的来说，当结点数较小时，四种方法之间差别不大。当数据量较大或打结比例较高时，除exact以外的三种近似方法的偏差增加，但运算时间无明显变化，而exact法的运算时间迅速增加。此时如果估计的精确性没有估计时间那么重要，Efron法以及Breslow法是不错的选择，其中，Efron法更为精确而Breslow方法倾向于低估正确的β值。如果时间上没有限制，可以选择Exact法和discretemodel，将得到更为精确的结果。

生存分析 Cox模型 打结数据 部分似然函数

Cox回归模型，或叫相对风险模型（Relative Risk Model）是目前生存分析中最为广泛使用的方法之一。该模型最早由Cox D.R在1972年提出。该模型无需对基准风险函数做任何的限制，是半参数模型，克服了生存分析传统的参数法和非参数法的局限性，目前广泛运用于不同治疗方法的比较以及各种疾病预后相关因素的研究[1]。

Cox模型在应用中还存在一些问题，其中之一就是数据存在结点时的处理方法。数据存在打结是指有多个个体有相同的失效时间。在实际应用中，由于失效时间往往是以一种离散的方式记录的，得到的数据存在打结是很普遍的。

失效时间不存在打结是Cox模型的一个重要假设，与模型的估计紧密相关，在该假设不满足时仍可以使用Cox模型，但需要对估计的方法进行改进。

目前有四种常见的方式用来处理打结数据，分别是 Exact model、discrete model、Efron 法以及 Breslow法。研究表明，Exact法和discrete model的结果较为精确，但是计算时间较长。Efron法以及Breslow法用时短，但参数估计偏差较大。Breslow方法计算比较简便，是目前大多数软件默认的处理Cox模型打结数据的方法，但是在R软件的survival包中，默认的方法是Efron法。

本文对四种不同的处理打结数据方法的原理进行讨论，并利用模拟讨论在不同样本量水平和打结程度下，在参数估计，估计量效率（efficiency of estimators），拟合统计量，计算时间方面的表现。最后结合具体数据进行展示。

1 方法介绍

Cox模型构建的思路是，所有研究对象的生存情况是多个影响因素共同作用的结果，可用风险函数表示，记为 λ(t;x)，其中 x=(x1,x2,…)′是基准协变量，在个体进入试验之前或进入试验之时已经测得，T是绝对连续的失效时间变量[2]。假设研究对象中影响生存的因素均不存在，其生存情况用λ0(t)表示，称为基础风险函数，那么，研究对象的实际生存情况，即λ(t;x)，是影响因素x在基础风险函数的基础上，进一步修改的结果，即风险函数可表达为：

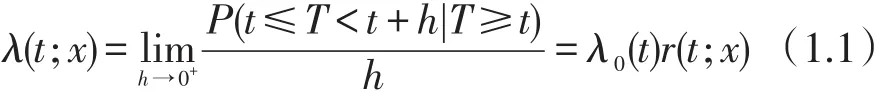
英国统计学家D.R.Cox于于1972年首次提出把r(t;x)构造为指数形式，即将风险函数写作（2.2）式：

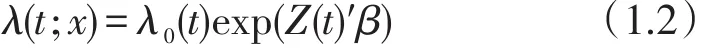
其中Z(t)=[Z1(t),…,Zp(t)]′是一个可能时间相依的协变量向量，是时间t和基准协变量的函数。Cox回归模型可以估计相对风险，例如所建立的回归模型包含组别变量，该变量是一个二分类变量，以1表示治疗组，0表示对照组，则治疗组与对照组风险函数的比值为

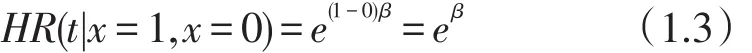
该比值的含义为，当其他变量相同时，在每个时间点，治疗组的死亡风险都是对照组的eβ倍。

对于定量数据的协变量，如年龄，HR的结果是：

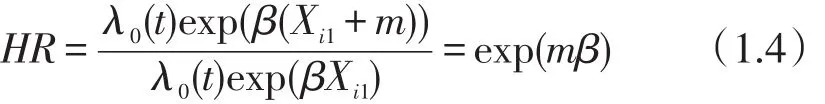
即该协变量每增长m单位，HR就要在原来的基础上乘以exp(mβ)。

Cox模型的假设之一是失效时间不存在打结，在该假设成立的前提下，参数估计可以通过部分似然（partial likelihood）方法得到[3][4]。

用zl表示第l个个体的解释变量，排序的失效时间为t1＜…＜tk。用Di={i1,…,idi}表示在ti时刻失效的个体组成的集合，Qi是{i1,…,idi}的di!个排列组成的集合，P=(p1,…pdi)是Qi中的一个元素，用di表示在ti时刻失效的个体数，用Ri表示在ti时刻的风险集。R(tj,P,r)=R(tj)-{p1,…,pr-1}。

根据Cox（1972）提出的方法，数据不存在打结时，估计β的部分似然的公式为（2.5）式：

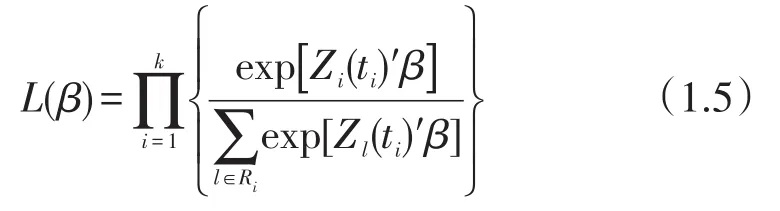
利用该方法估计参数时，似然函数的计算依赖于事件发生的顺序，个体的失效时间必须是有序的，如果有两个个体（例如A和B）有着相同的失效时间，在这种情况下，无法确定其中一个（如A）失效时，B是否在该时刻的危险集中。

当数据存在结点时，Kalbfleisch and Prentice（2002）[5]提出的exact法考虑在每个存在打结的时间点上事件发生的所有可能的排序。在tj处将结点分解成各种可能的情形后的平均部分似然为：

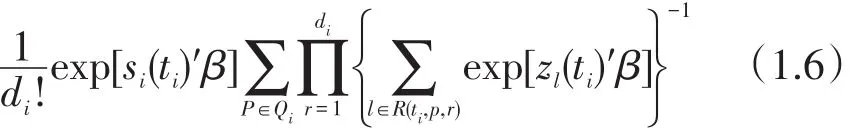
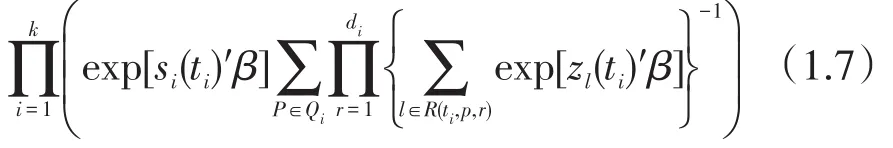
当每一个失效时间点的结点数目比较大时，上式的计算量会非常大。此时，可以对似然函数进行近似。Breslow(1974)[6]提出的近似似然函数为

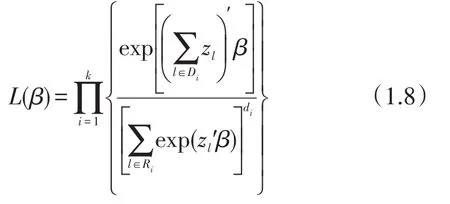
Efron方法(1977)[7]提出的似然函数为

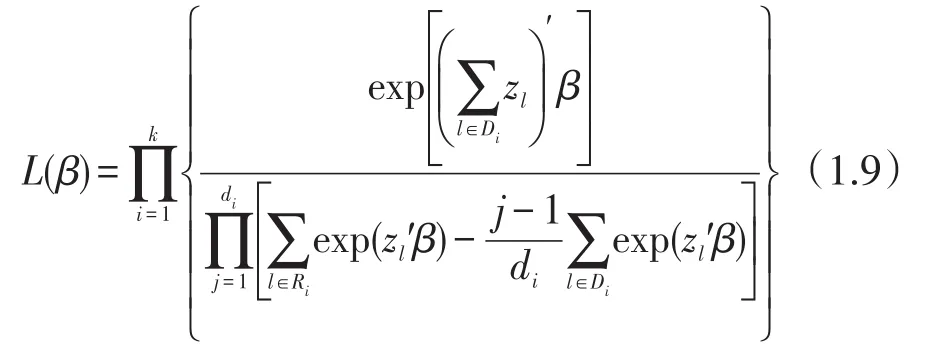
另外，当数据打结的比例较大时，可以考虑将失效时间看作离散变量。Cox（1975）建议利用离散Logistic模型（也叫条件logistic模型）：

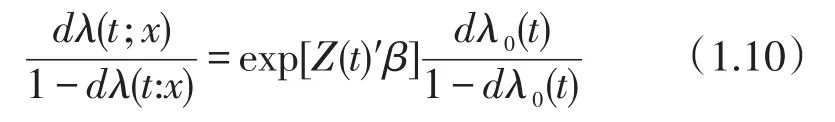
其中dλ0(t)是一个未指定的离散风险函数，在观测失效时间点t1＜…＜tk有值，将没有结点情形下的部分似然进行推广，得到以下部分似然函数。

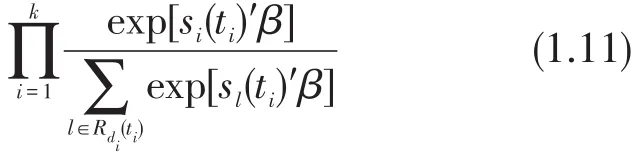
其中Rdi(ti)是从风险集R(ti)中挑出di个个体的所有子集组成的集合，l=(l1,…,ldi)是 Rdi(ti)的一个元素，

Kalbfleisch和 Prentice（2002）指出，Efron法和Breslow法对参数的估计存在偏差，且的方差估计值是不一致的。模拟显示，当diRi的值较大时，Breslow法对参数的估计会有较大的偏差。结点数很少时，三种方法得到相似的结果，不存在结点时，三种方法会得到完全一样的结果[5]。

2 数据模拟

本文采用模拟比较Exact方法和三种近似方法在参数估计，估计量效率（efficiency of estimators），拟合统计量和计算时间方面的差异。对于计算时间，使用每种方法重复10次估计，以得到平均计算时间。

生成两组数据，一组是失效时间服从指数分布的生存时间数据，即风险函数为：

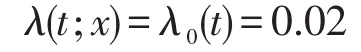
另一组是与该组基础风险函数相同，HR是e-1的生存时间数据，风险函数为

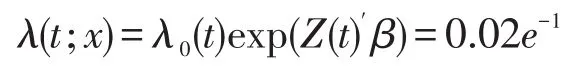
另外，是否删失的设置与生存时间独立，即生成的数据包括的变量为：生存时间，组别（0,1），是否删失（0,1）。

首先在每组1 000个个体的样本量水平上进行模拟。利用数据分组制造结点，分别将数据分到k=50,200,500个时间区间中去来制造高、中、低三种打结水平。具体方法是用生存时间数据落入的区间的右端点来代替原先的数据以制造结点。

利用SAS9.4中的PHREGPRocedule拟合模型。

当样本量为每组1 000个个体时，在结点数最多即k=50，平均每个时间点有20人的情形下，各种方法的计算时间均小于0.5秒，因此不再对计算时间进行记录和比较。

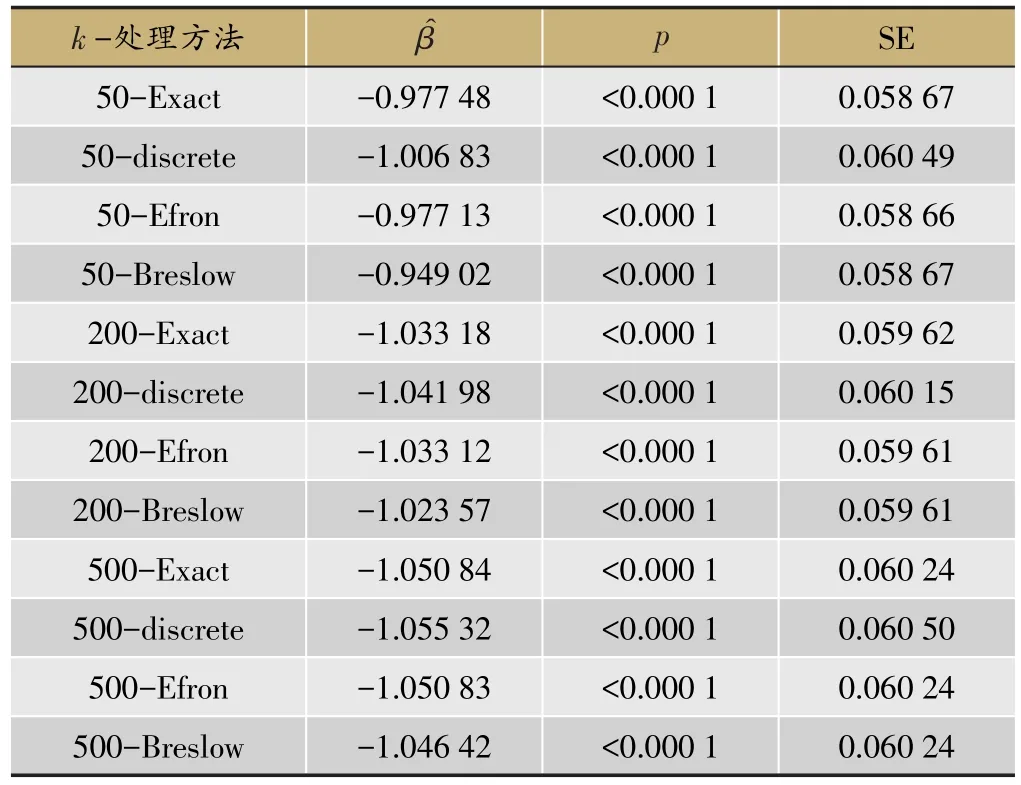
表1 n=1 000 β=-1 Cox模型模拟结果

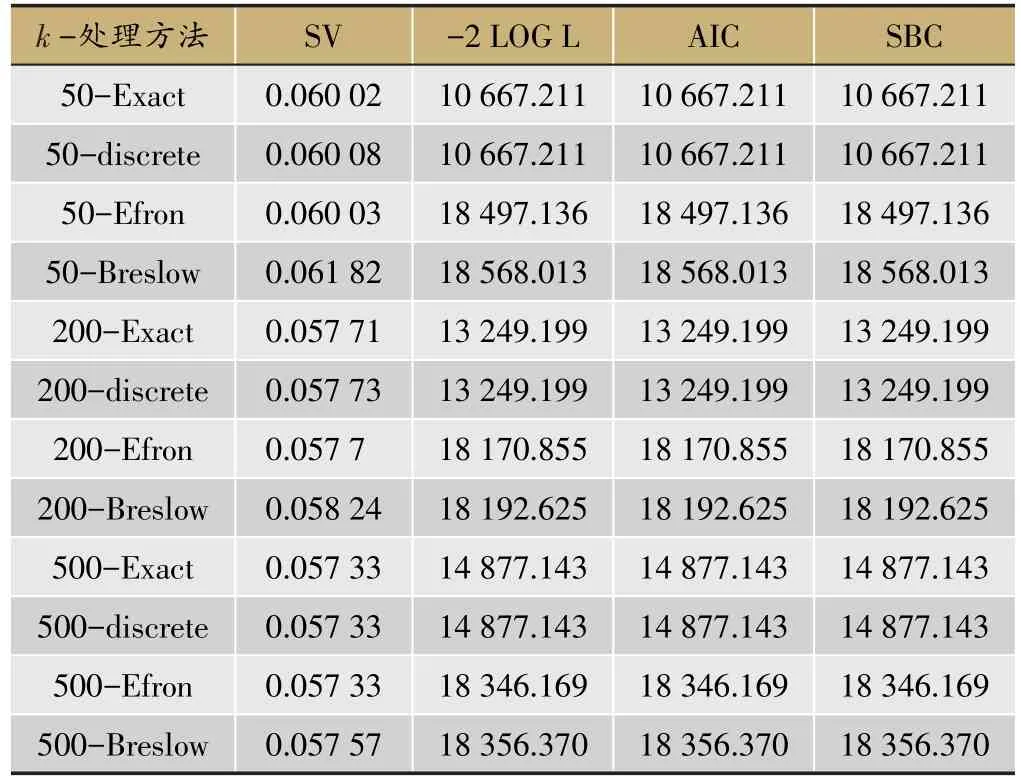
表2 n=1 000 β=-1 Cox模型模拟结果

表2展示了四种处理方法处理三种打结水平的SV和三种拟合统计量结果。其中SV（standardized measuresof variability）的定义为：

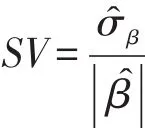
该统计量可以用来衡量参数估计值的有效性（efficiency of estimators）。

可以看到，Breslow方法在三种打结程度均有着最高的SV值，在参数估计值的有效性方面表现较差，其他三种方法之间不存在明显差异。

在拟合统计量方面，discrete model和Exact法的表现最好，其次是Efron法，Breslow法的结果最差。

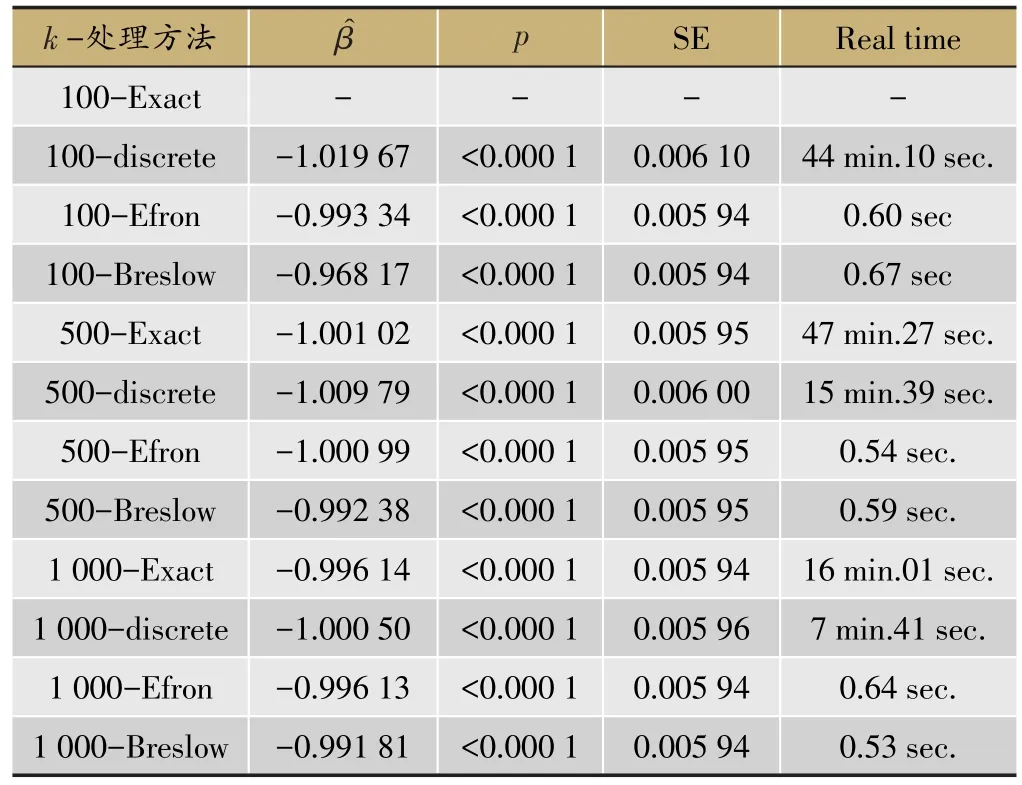
表3 n=100 000 β=-1 Cox模型模拟结果

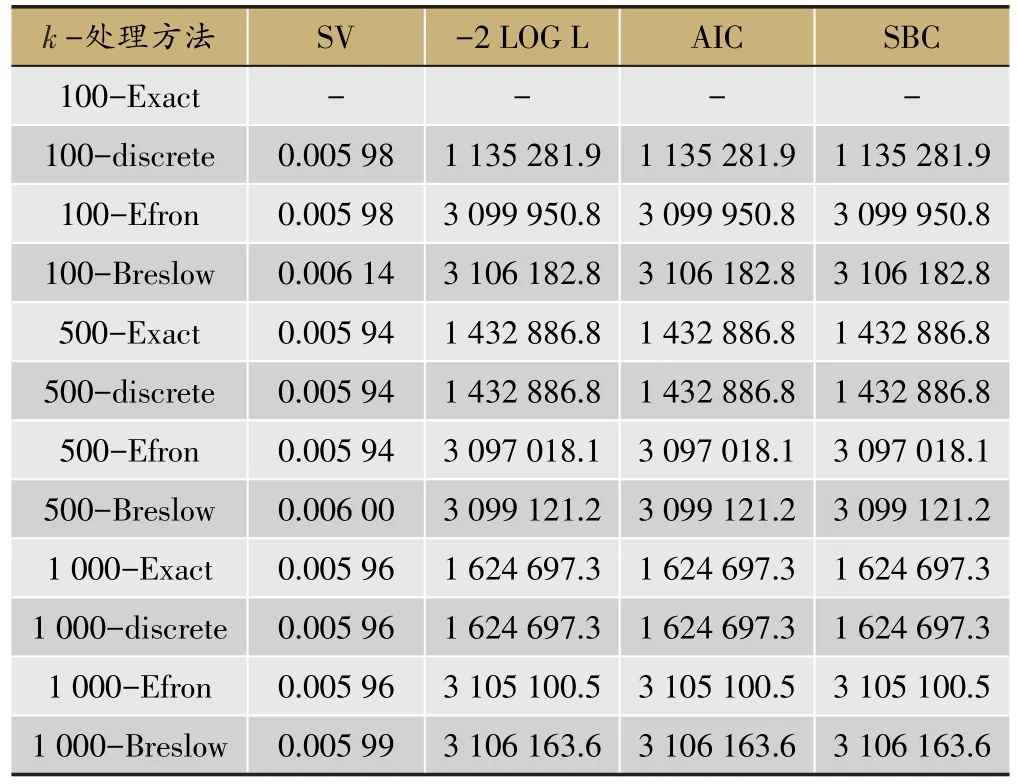
表4 n=100 000 β=-1 Cox模型模拟结果

表5 数据打结情况

在每组100,000个个体的样本量水平上进行模拟，样本量变大本身也会导致结点数增加，设置了k=100,500,1 000三个打结水平。

表4展示了四种处理方法处理三种打结水平的SV和三种拟合统计量结果。

Breslow方法在三种打结程度均有着最高的SV值，在参数估计值的有效性方面表现较差，其他三种方法之间不存在明显差异。在拟合统计量方面，the discrete model和Exact法的表现最好，Efron法和Breslow法的结果几乎是另外两种方法的3倍。

4 实际应用

某医院采用随机对照临床研究方法，纳入晚期结直肠癌患者60例，经过数据处理有效数据共53例。其中23人的治疗结局为死亡，30人的治疗结局为未死亡，即有56.6%的数据右删失。两组均采用常规治疗(营养支持、化疗、对症、中医)，治疗组在此基础上加用某中药,对照组加用安慰剂胶囊，治疗一段时间后进行随访，观察两组患者的生存期情况。

数据中主要考虑的指标包括：组别（治疗组=1，对照组=0），性别（女=1，男=0），年龄，患病阶段（阶段1、阶段2、阶段3、阶段4），是否死亡，OS生存期（单位：月）。其中OS生存期数据存在结点，具体情况如表5所示。这种情况下，运用Cox模型比较两组的治疗，必须考虑打结数据的处理。表6至表10是四种方法处理该数据的结果。

表7是p值结果。由表可以看出，Breslow得到的p值较大。

表8是参数估计的标准误。由表可以看出，Exact法，Breslow法和Efron法的结果无明显差异，Discrete法得到的标准误与其他三种方法相比略大一些。

表9是SV结果，由表可以看出，Breslow法在四个协变量上的结果均是最差的，另外三种方法不存在明显差异。

表9是拟合统计量结果，由表可以看出，Exact法结果最好，discrete法与Exact法差别不大，Breslow法和Efron法结果较差。

该数据有较多结点，但由于样本量小，四种方法的计算时间都很短，推荐使用Exact法以得到更精确的结果，如果软件（如R）中不包含该方法，则推荐Efron法，该方法估计的结果与Exact法最接近，而其余两种方法偏差较大。

5 结论

样本量较小的情形下（n≤1000），不同程度的打结，四种方法的估计时间都很短，此时Breslow法会低估参数绝对值且偏差较大，Efron法表现好于Breslow法，discrete法会高估参数绝对值。但还是建议使用Exact法来获得最为精确的估计，R软件的survival包没有包括该方法，可以使用SAS软件的PHREG PRocedule，选择“exact”即可。

样本量较大的情况下（n≥100,000），Exact法的计算时间迅速增加，打结程度高时个人的电脑可能出现内存不足无法利用SAS运算该方法的情形，此时可以考虑使用discrete法，计算时间不到Exact法的一半。考虑到样本量较大，各种方法的偏差都小，更推荐使用Breslow法和Efron法，在样本量为100,000且打结程度最高时（平均每个时间点有1 000个个体），运算时间仍不超过1秒钟，其中Efron法更加精确。如果时间上没有限制，可以使用Exact法或discrete法，可以得到更好的拟合统计量结果和更准确的参数估计结果。

表6 实际数据拟合Cox回归模型

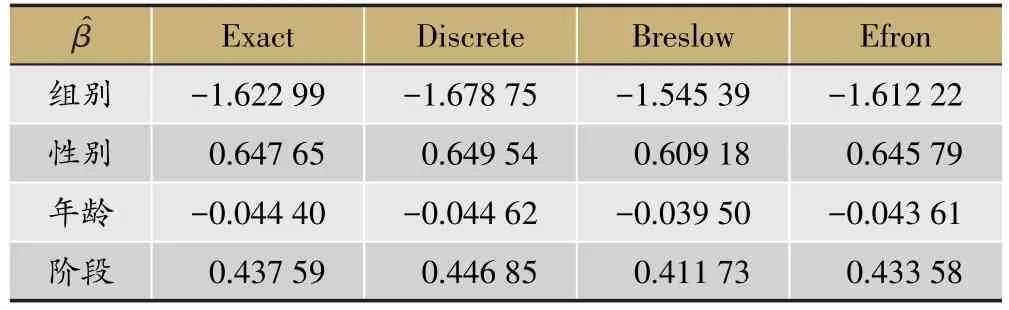
表6 实际数据拟合Cox回归模型

?

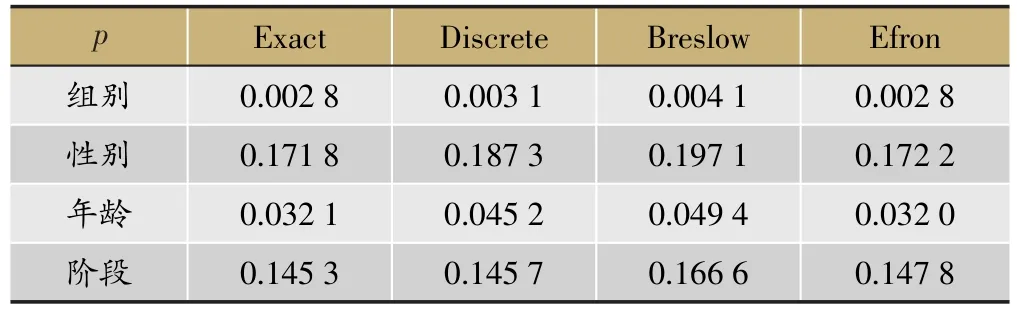
表7 实际数据拟合Cox回归模型p

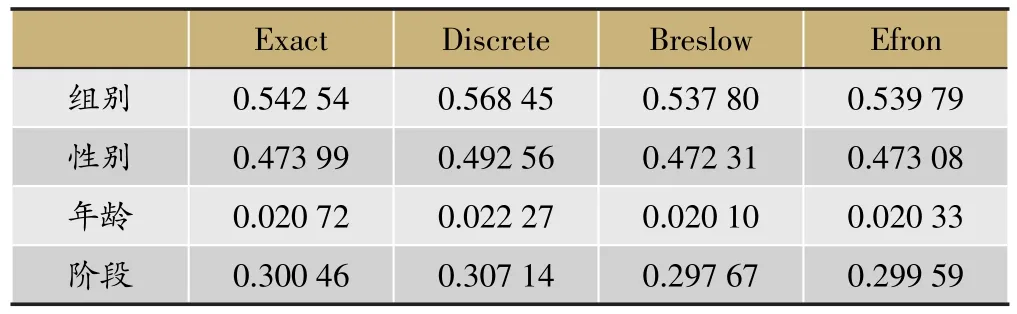
表8 实际数据拟合Cox回归模型SE

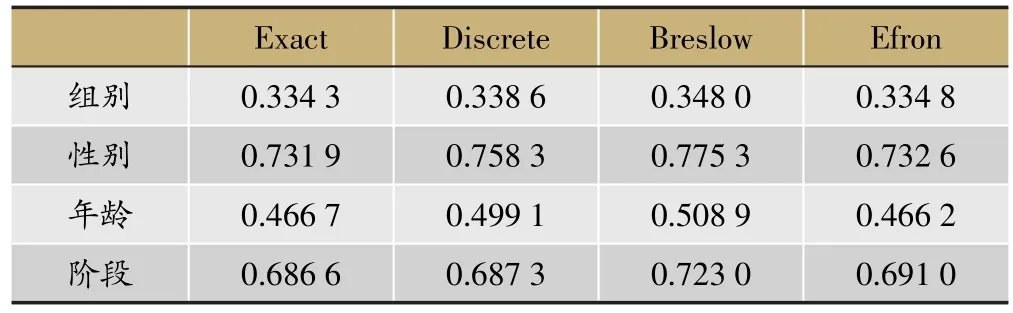
表9 实际数据拟合Cox回归模型SV

1 陈兵,骆福添.生存分析中的回归模型.中国卫生统计,2006,23(5):462-465.

2 金丕焕,陈峰.医用统计方法.复旦大学出版社,2009:378-385.

3 Cox DR.Regression Models and Life-Tables.JRoy Stat Soc,1972,34(2):187-220.

4 Cox D.R.Partial likelihood.Biometrika,1975,62(2):269-276.

5 Kalbfleisch J D,Prentice R L.Marginal likelihoods based on Cox's regression and lifemodel.Biometrika,1973,60:267-279.

6 Breslow N.Covariance analysis of censored survival data,Biometrics,1974,30:89-99.

7 Efron B.The efficiency of Cox's likelihood function for censored data.J Am Stat Assoc,1977,72,557-565.

8 Hertz P I,Rockhill B.Validity and Efficiency of Approximation Methodsfor Tied Survival Timesin Cox Regression.Biometrics,1997,53(3):1151-1156.

9 Borucka J.Methods of Handling Tied Events in the Cox Proportional Hazard Model.Ieee,2014,2(2):92-106.

Discussion on Methodsfor Tied Survival Timesin Cox Model

Zhang Wenli1,2,Zhang Tong3,Yi Danhui1,2,Yang Yufei3
(1.Center for Applied Statisticsof Renmin University of China,Beijing 100872,China;2.School of Statistics,Renmin University of China,Beijing 100872,China;3.Xiyuan Hospital of China Academy of Chinese Medical Sciences,Beijing 100091,China)

Cox regression model is one of the most widely used methods in the survival analysis.One assumption of this model is that there is no tie in the failure times,that is,individual has different failure times.In practical applications,the existence of ties in time data is very common.In this paper,four common methods of dealing with ties in Cox model,including Exact method,discrete model method,Efron method and Breslow method,were compared with simulation.The results showed that Exact method and discrete model were the best,but they took the longest time.Efron method and Breslow method were faster but there was a greater deviation in parameter estimation.Moreover,the sample amount and ties degree also affect the results.In general,when there are a few ties,the difference between four methods was small;and in the case of large datasets or a large number of ties,the biasof three approximation methodsincreased except Exact method.However,there was no significant change on computational time.While the computational time of the Exact method increased rapidly.Therefore,if the estimation precision is not as important as the estimation time,Efron method and Breslow method will be good choices.Efron method is more preferably as it is more precise.And Breslow method tends to underestimate the trueβ.If there is no limit in time,Exact method and discrete model can be chosen to achieve more accurate results.

Survival analysis,Cox model,tied data,partial likelihood function

10.11842/wst.2017.09.007

R33

A

2017-05-18

修回日期：2017-08-23

＊ 中国人民大学2017年度‘中央高校建设世界一流大学（学科）和特色发展引导专项资金’，负责人：易丹辉；和教育部人文社会科学重点研究基地重大项目(16JJD910002)：基于大数据的精准医学生物统计分析方法及其应用研究，负责人：？？。

＊＊ 通讯作者：易丹辉，中国人民大学教授，博士生导师，主要研究方向：风险管理与保险、预测与决策。杨宇飞，博士生导师，中国中医科学院西苑医院肿瘤诊治部主任、主任医师，主要研究方向：中西医结合癌症治疗。

（责任编辑：张娜娜，责任译审：王 晶）