多个响应变量的纵向数据联合建模方法及应用＊

林存洁，吴 朦，易丹辉，胡镜清＊＊

（1.中国人民大学应用统计科学研究中心，北京100872；2.中国人民大学统计学院，北京 100872；3.中国中医科学院中医基础理论研究所，北京 100700）

多个响应变量的纵向数据联合建模方法及应用＊

林存洁1,2，吴 朦3，易丹辉1,2，胡镜清3＊＊

（1.中国人民大学应用统计科学研究中心，北京100872；2.中国人民大学统计学院，北京 100872；3.中国中医科学院中医基础理论研究所，北京 100700）

纵向观测过程中经常会遇到对同一个个体测量多个响应变量的情况，由于同一个个体的不同响应变量之间存在一定的相关性，因此独立分析每一个响应变量将会损失相关信息。本文利用联合建模的方式对多个响应变量建立混合效应模型，通过不同响应变量的随机效应之间的相关性刻画不同响应变量之间的关系，并利用极大似然方法给出模型中参数的估计，最后通过中风病的实际数据分析来说明该方法的应用。

多元纵向数据 线性混合效应模型 联合模型 随机效应

在临床试验、生物医学和社会科学等研究领域中，经常会对不同的个体在一段时间内进行重复测量，从而得到纵向观测数据。虽然不同个体之间的观测彼此独立，但是同一个个体的不同观测之间存在一定的相关性，因此纵向数据分析的一个重要研究内容就是如何考虑个体内的相关性。其中，最常用的统计模型之一是线性混合效应模型[1]，该模型通过引入随机效应来刻画个体在不同观测点之间的关系；后来该模型的思想被拓展到非线性混合效应模型[2]以及广义线性混合效应模型[3]等。近年来这些模型被广泛应用于单个响应变量的纵向数据分析中[4,5,6]。

目前关于纵向数据的研究，大部分集中于单个响应变量的分析方法。但是在很多情况下，单个响应变量不能够全面描述个体的情况，因此对同一个个体会测量两个或多个响应变量，即得到多个响应变量的纵向观测数据。例如，在对中风病气虚血瘀证的中医复杂干预研究中，需要评价中医介入治疗和单纯西医治疗的疗效差异，由于中风病的治疗方式多样，常常有“多作用、多靶点”的效果，因此对于中风病的疗效评价指标有很多种。从中医角度出发，有1986年制定的《中风病中医诊断、疗效评定标准》、1994年制定的《中风病辨证诊断标准（试行）》、1996年制定的《中风病诊断与疗效评定标准（试行）》以及2011年制定的《缺血性中风证候要素诊断量表》。另一方面，现代医学对脑卒中的评价指标又有神经功能缺失评定指标（NIHSS）、功能预后指标（Brunnstrom）等。对于同一个患者而言，不同的指标反映不同方面的信息，因此不同的指标之间必然存在一定的相关信息。如何准确刻画和利用不同响应变量之间的相关信息来提高估计的准确性，是多个响应变量的纵向数据分析研究的重点。

近年来，关于多个响应变量的纵向数据分析方法也成为研究的热点。一种方式是将多个纵向观测响应变量降维成一个响应指标变量，然后利用单个响应变量的纵向数据分析方法进行分析。该方法容易理解和实现，但是需要选择合适的降维方法，而最常用的主成分分析的方法不能完全提取原始数据的信息，另外降维之后的指标不一定有很好的解释意义。另外一种方式是通过引入潜在变量的方式将多个响应变量联系起来[7,8,9,10]，并利用EM算法实现模型的估计，该方法需要基于一些关于潜在变量的假设，但是这些假设是难以验证的。第三种方式则是基于混合效应模型的联合建模方法[11,12,13,14,15]，该方法通过对每个响应变量的纵向观测过程假设一个随机效应，进而利用不同随机效应之间的联合分布刻画不同响应过程之间的关系。本文将采用一般混合效应联合建模方法对多个响应变量的纵向观测数据进行分析，并给出估计方法。

本文的第二部分介绍了混合效应的联合模型和估计方法；在第三部分将方法应用于中风病的疗效评价；第四部分是本文的总结和讨论。

1 多个响应变量的联合模型及其估计

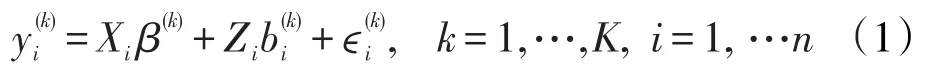
我们可以通过向量拉直的方式将模型（1）转化成一般的纵向数据混合效应模型。令为个体i的K个响应指标的观测向量，为niK×1维的向量，为pK×1维固定效应向量，bi=为qK×1维随机效应向量，定义=diag(Xi,…,Xi)为 niK×pK 的矩阵，=diag(Zi,…,Zi)为niK×qK的矩阵，则模型（1）等价于下列线性混合效应模型：

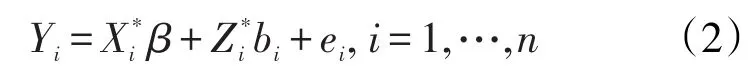
对于一般的线性混合效应模型的估计，文献中已经有很多方法，如Laird&Ware（1982）介绍了极大似然估计方法，并给出EM算法，同时给出了带有限制的极大似然估计（RMLE）和相应的计算方法。对于模型（2），我们应用类似的估计方法。具体来说，因为Yi∼，因此我们很容易写出对数似然函数：

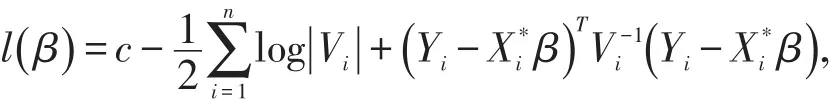
其中c为常数项。如果协方差阵Vi是已知的，则可以利用极大似然估计得到β和bi的估计：

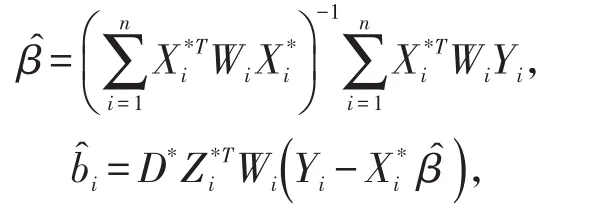
其中Wi=。但是协方差阵往往是未知的，即和Ri中含有一些未知参数（我们用θ表示），那么我们可以关于 β和θ同时极大化似然函数，即得到极大似然估计。进而可以利用经验贝叶斯的方法得到的估计

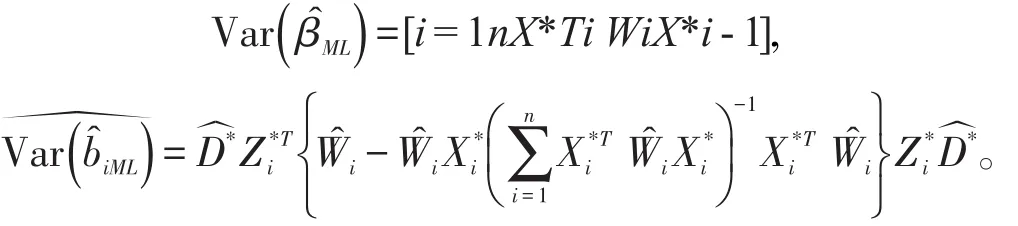
可以证明该估计是相合的，而且是渐近正态的，其估计的方差可以用如下方式进行估计：而且当随机效应的联合分布可以准确刻画不同的响应变量之间的相关性时，联合建模的方式可以有效提高估计的准确性。另外，当K的值比较大的时候，计算量会比较大，可以利用成对似然估计的方[16]对参数进行估计。

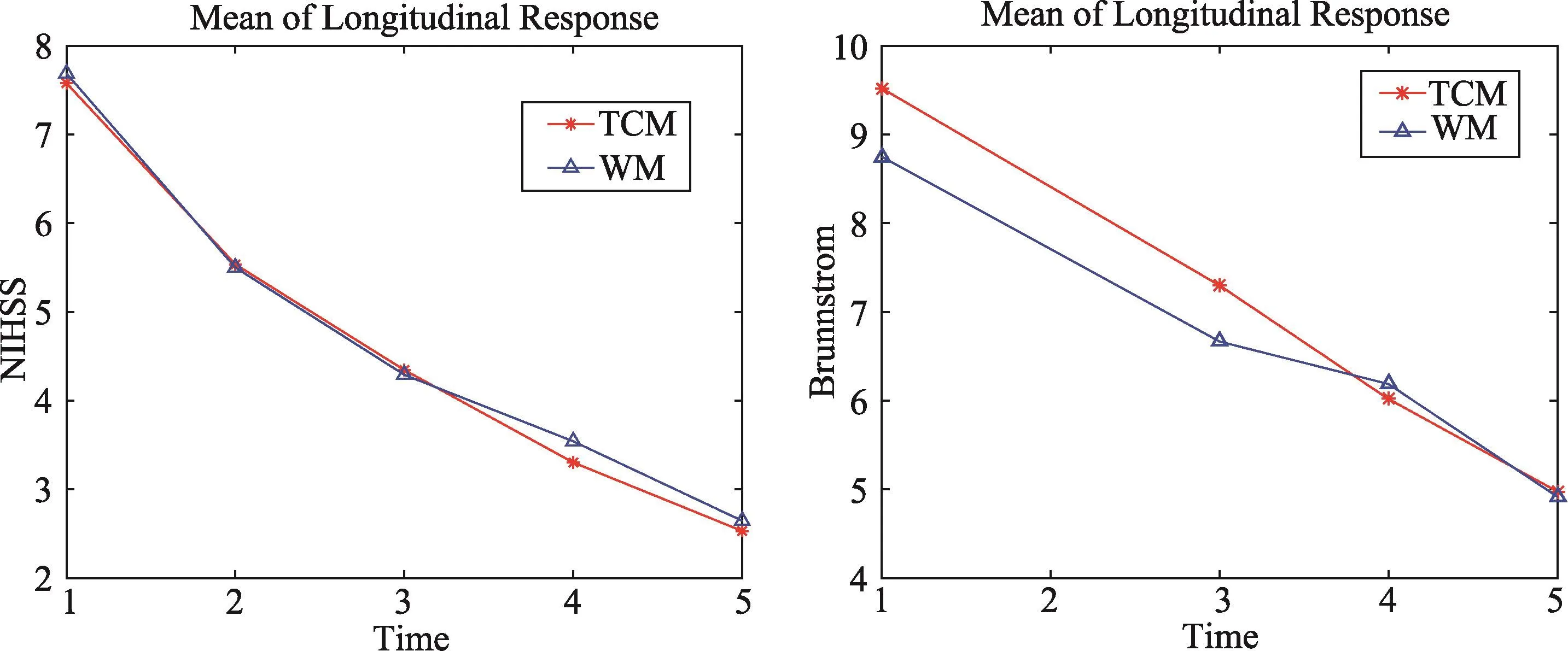
图1 313例患者的NIHSS评分和Brunnstrom评分均值走向图

2 实例分析

在本节中我们将上述方法应用到中风病气虚血瘀证中医复杂干预的研究中。该研究选取313例中风病（急性缺血性脑卒中）患者作为研究示范病例，旨在分析中西医联合治疗的效果。数据中记录了患者的基本信息和中西医日常诊疗信息。患者被随机分配到试验组和对照组，对照组的患者采用西医标准治疗，试验组的患者在原来西医标准治疗的基础上，加用丹红或参麦注射液。所采用的疗效评价指标有美国国立卫生研究院卒中量表（National Institute of Health Stroke Scale，NIHSS）、Barthel指数（Barthel Index，BI）、改良Rankin量表（Modified Rankin Scale，MRS），Brunnstrom Scale评分以及中医证候评分（参照1994年的《中风病辨证诊断标准（试行）》）等。我们以NIHSS和Brunnstrom评分为例，分析不同治疗方法的效果。首先对NIHSS评分和Brunnstrom评分作均值图，如图1。图中Treatment=1表示试验组，Treatment=0表示对照组。从该图可以看出，观测初始点时试验组的两种评分都略高于对照组的评分，随着治疗时间的推移两种评分都在下降，但是最后一次观测时间点的对照组的评分却略高于试验组的评分，尤其是Brunnstrom评分，最后的差异更大。这说明中西医结合治疗方案的治疗效果可能会更好。

为了更加准确地分析治疗方法的效果，利用联合建模方法对NIHSS评分和Brunnstrom评分进行综合分析，建立如下联合模型：

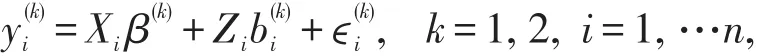
这里考虑的协变量Xi有时间、治疗方案分组（0=对照组，1=实验组）、时间和治疗方案分组的交互项、性别（0=男性，1=女性）、年龄、BMI指数、合并疾病（这里指合并三高和冠心病的情况，0=未合并其他疾病，1=入组时已合并其他疾病）、中风的初发与复发情况（0=初发，1=复发）、气虚血瘀证评分是否≥7分（0=否，1=是），考虑的随机效应的协变量Zi为时间变量。具体估计结果见表1。从表1可以看出，对于NIHSS和Brunnstrom评分而言，时间的系数估计值分别为-1.517和-0.996，且估计的p值都很小（＜0.05），这说明随着治疗时间的推移，对照组患者的NIHSS评分和Brunnstrom评分都会显著地降低，即西医治疗方案能够缓解中风病情。治疗方案分组的估计系数分别为0.03和1.124，p值为0.926和0.061，这表示在观测初始点时试验组患者的NIHSS评分均值和Brunnstrom评分的均值比对照组患者的NIHSS评分均值和Brunnstrom评分的均值要高，但差异并不显著。分组*时间的系数估计值分别为-0.018和-0.416，这说明随着时间的变化，试验组患者的NIHSS评分和Brunnstrom评分分别比对照组的NIHSS评分和Brunnstrom评分降低地更快，但是NIHSS评分的差异不显著（p值为0.873），而Brunnstrom评分的差异显著（p值为0.010）。这说明中西医结合治疗方案能够更快的缓解病情，这些结论和图1的结论也相吻合。除此之外，其它变量的系数估计结果可以看出，对于NIHSS评分而言，在其他影响因素相同的情况下，女性患者比男性患者的NIHSS评分要高，年龄越大的患者NIHSS评分也会越高，肥胖的患者评分也会越高，但是这些差异不显著；合并疾病是一个显著的影响因素，即有其他合并疾病的患者比未合并其他疾病的患者NIHSS评分的均值要低；另外复发患者以及气虚血瘀证严重的患者其NIHSS评分也会越高，不过差异并不显著。对于Brunnstrom评分，显著的影响因素是年龄，即老年患者的评分要显著的高于其它患者的评分，而其他因素都不显著。

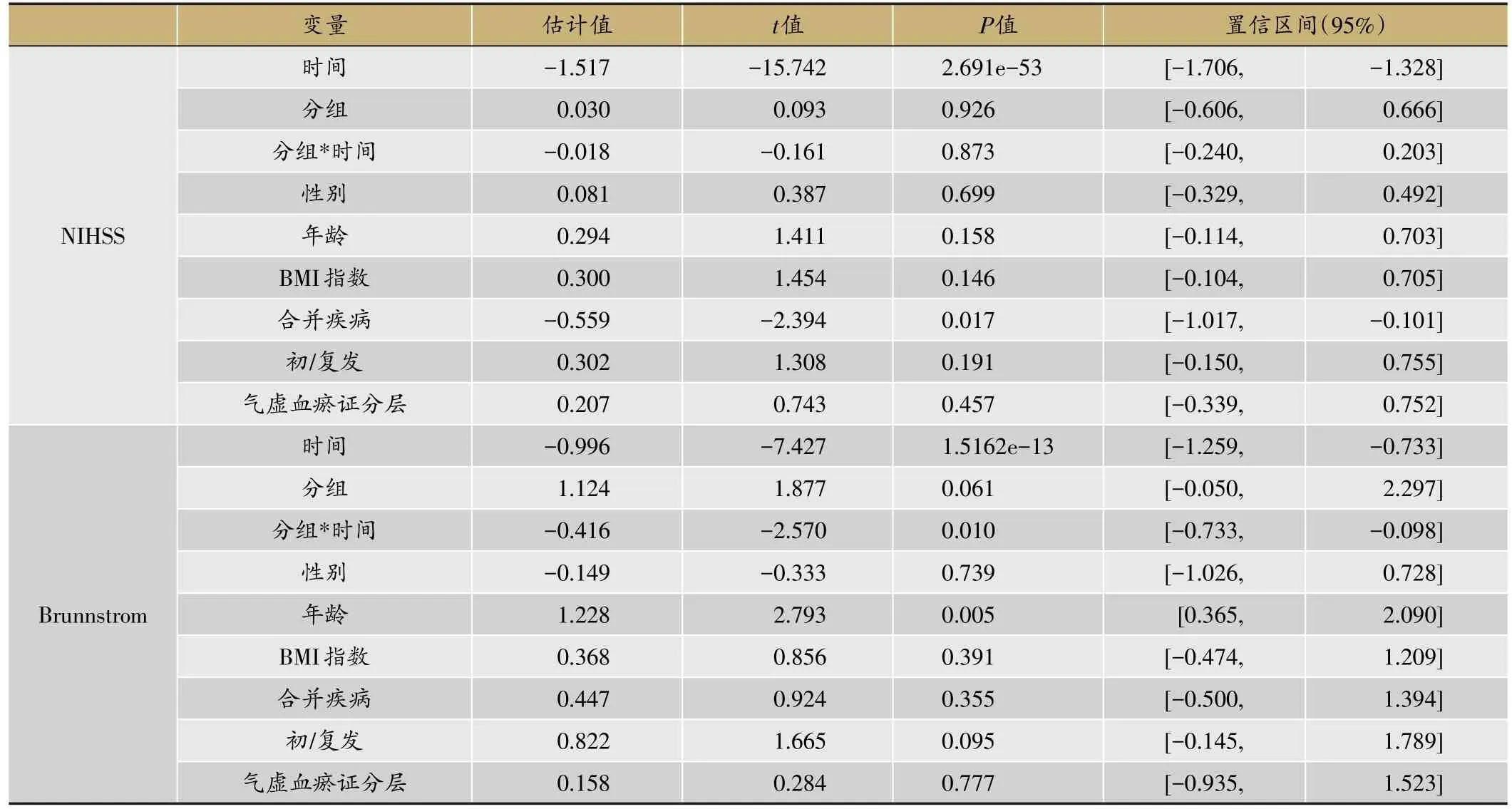
表1 NIHSS与Brunnstrom联合建模估计结果（313例）

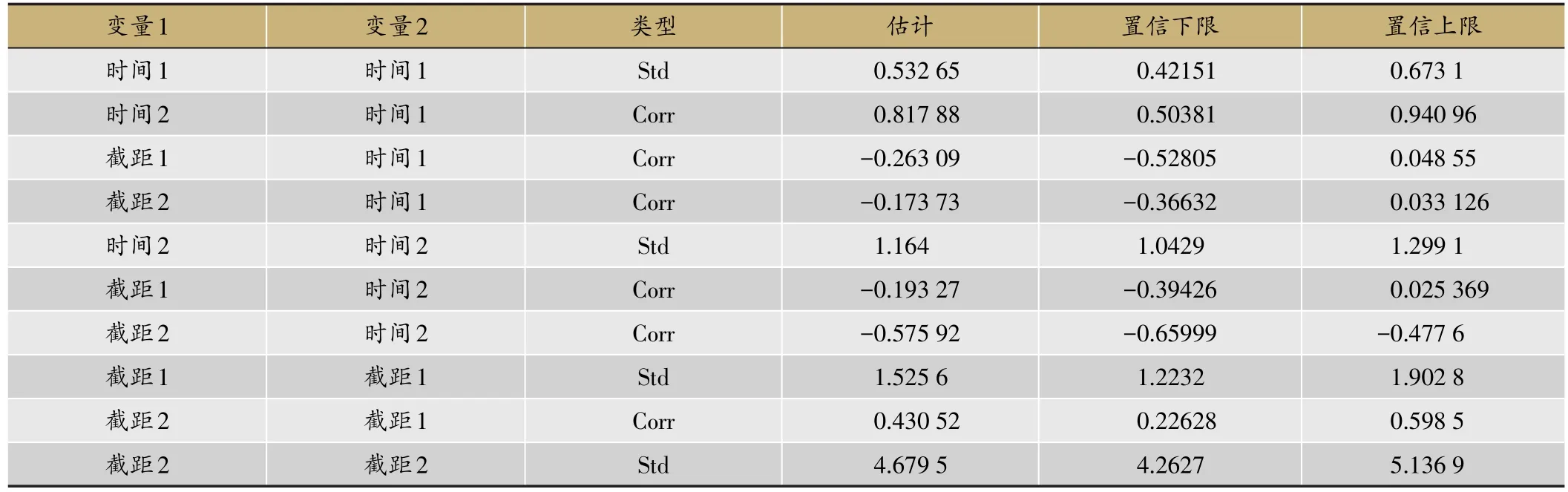
表2 随机效应的相关性和估计

为了检验NIHSS评分和Brunnstrom评分之间的相关性，我们检验随机效应的显著性以及不同响应过程之间随机效应的相关性。表2展示了混合效应模型中随机效应的方差估计和相关系数估计，从该表的结果可以看出NIHSS评分的随机效应和Brunnstrom评分的随机效应都是显著不为0（置信上下限不包含0），其中和表示随机效应的截距项，和表示时间的随机效应。而且NIHSS评分的时间随机效应和Brunnstrom评分的随机效应具有显著的线性相关性，NIHSS评分的截距项随机效应和Brunnstrom评分的截距项随机效应也具有显著的线性相关性。图2展示了随机效应的估计散点图，从图中也得出相同的结论。这也说明了NIHSS评分和Brunnstrom评分之间确实存在一定的相关性。

3 小结

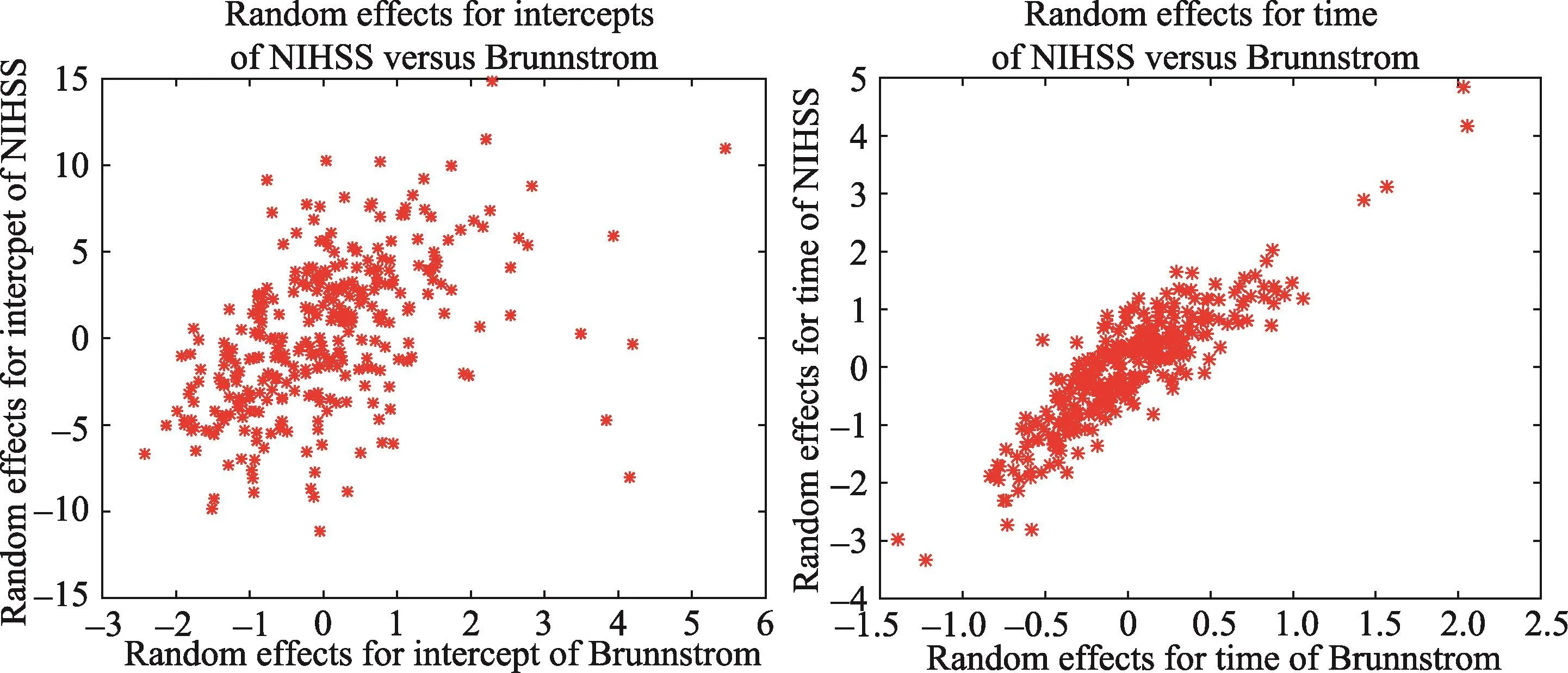
图2 NIHSS评分和Brunnstrom评分的随机效应图

本文针对多个响应变量的纵向观测数据的建模方法进行了讨论。由于同一个个体的不同响应变量之间存在一定的相关性，如果分别分析每个响应变量而忽略不同响应变量之间的关系，可能会得到错误的结论。因此，我们提出利用联合建模的方式对此类数据进行分析，通过对每个响应变量建立一般线性混合效应模型，并利用随机效应之间的相关性刻画不同的响应变量之间的关系，进而充分利用数据中的信息提高估计的精确性。为了估计模型中的参数，将数据拉直得到一般的线性混合效应模型，然后利用极大似然方法给出模型中参数的估计。最后通过中风病的数据说明该方法的应用。如果单独对NIHSS评分建立线性混合效应模型会发现，显著的变量有时间、年龄和合并疾病，如果单独对Brunnstrom评分建立线性混合效应模型，显著的变量则是时间和年龄。但是通过NIHSS评分和Brunnstrom评分的联合建模发现分组*时间是Brunnstrom评分的显著变量，这也说明试验组的患者病情缓解地更快。因此借助于联合建模的方式可以更加准确的评价不同治疗方式的效果。除了考虑两个响应变量的联合建模过程，我们还可以考虑NIHSS评分、Brunnstrom评分和其它评价指标的联合建模，如Barthel指数、中医证候评分等。如果响应变量的个数比较多，我们可以考虑利用成对似然方法进行估计。

1 Laird N,Ware J.Random-effects models for longitudinal data.Biometrics,1982,38:963-974.

2 Davidian M,Giltinan D.Nonlinear models for repeated measurement data.New York:Chapman&Hall,1995.

3 Breslow N,Clayton D.Approximate inference in generalized linear mixed models.JAm Stat Assoc.1993,88:9-25.

4 Fitzmaurice G,Laird N,Ware J.Applied Longitudinal Analysis.Wiley,New York,2004.

5 Hedeker D.,Gibbons R.D.Longitudinal Data Analysis.Wiley,Hoboken,New Jersey,2006.

6 Diggle P J,Heagerty P,Liang K Y,et al.Analysis of Longitudinal Data.New York:Clarendon Press,2002.

7 Chan D.The conceptualization and analysis of changeover time:An integrative approach incorporating longitudinal mean and covariance structures analysis(LMACS)and multiple indicator latent growth modeling(MLGM).Organiz Res Meth.1998,1:421-483.

8 Roy J,Lin X.Latent variable models for longitudinal data with multiple continuousoutcomes.Biometrics,2000,56:1047-1054.

9 Blozis S.A second-order structured latent curve model for longitudinal data.In:van Montfort K,Oud H and Satorra A(eds)Longitudinal models in the behavioural and related sciences.Mahwah,New Jersey:Lawrence Erlbaum Associates,2006:189-214.

10 Harring J.A nonlinear mixed effects model for latent variables.J Educ Behav Stat,2009,34:293-318.

11 Shah A,Laird N,Schoenfeld D A random-effects model for multiple characteristics with possibly missing data.J Am Stat Assoc,1997,92:775-779.

12 Schafer JL,Yucel RM.Computational strategies for multivariate linear mixed effects modelswith missing values.JComput Graph Statist,2002,11,437-457.

13 Fieuws S,Verbeke G.Joint modelling of multivariate longitudinal profiles:Pitfalls of the random-effects approach.Stat Med,2004,23:3093-3104.

14 Roy A.Estimating correlation coefficient between two variables with repeated observations using mixed effects model.Biom J.2006,48:286-301.

15 Wang W,Fan T.Estimation in multivariate t linear mixed models for multiplelongitudinal data.Stat Sinica,2011,21:1857-1880.

16 Fieuws S.,Verbeke G.Pairwise fitting of mixed models for the joint modeling of multivariate longitudinal profiels.Biometrics.2006,62:424-431.

Joint Modeling of Multivariate Longitudinal Data and Its Application

Lin Cunjie1,2,Wu Meng3,Yi Danhui1,2,Hu Jingqing3
(1.Center for Applied Statistics,Renmin University of China,Beijing 100872,China;2.School of Statistics,Renmin University of China,Beijing 100872,China;3.Instituteof Basic Theory for Chinese Medicine,China Academy of Chinese Medical Sciences,Beijing 100700,China)

Multiple outcomes measured repeatedly for the same subject are common in longitudinal observation.If we use the approach by analyzing each outcome separately,it may lead to wrong conclusions due to the failure of accounting for joint evolution of different outcomes.To adequately capture the interdependence among multiple outcomes,we proposed a joint modeling for multivariate longitudinal data by constructing a linear mixed-effects model for each outcome and accommodating the relationship among multiple outcomes through correlation in random effects.Maximum likelihood method was adopted to estimate parameters in this model.The application of this method was demonstrated through the analysisof strokedata.

Multiplelongitudinal data,linear mixed-effectsmodel,joint modeling,randomeffects

10.11842/wst.2017.09.006

R33

A

2017-05-23

修回日期：2017-07-25

＊ 中国人民大学2017年度中央高校建设世界一流大学（学科）和特色发展引导专项资金（297217000021），负责人:易丹辉；教育部人文社会科学重点研究基地重大项目（16JJD910002）：基于大数据的精准医学生物统计分析方法及其应用研究，负责人：易丹辉；国家中医药管理局中医行业科研专项（201207005）：30种疾病中医临床评价规范与复杂干预评价共同路径研究，负责人：胡镜清。

＊＊ 通讯作者：胡镜清，研究员，博士生导师，主要研究方向：适应中医药理论构筑与诊疗模式的临床研究方法研究。

（责任编辑：张娜娜，责任译审：王 晶）