碳税下回收品不同质量水平制造/再制造企业运作策略研究

(上海理工大学 管理学院,上海 200093)

碳税下回收品不同质量水平制造/再制造企业运作策略研究

王心月,郭健全

(上海理工大学 管理学院,上海 200093)

在回收品不同质量水平的情况下,研究制造/再制造企业不同碳税下的最优运作。在多周期闭环混合系统中,需求由质量无差异的新产品和再制造品共同满足。假设回收品质量水平服从标准正态分布,回收成本、再制造成本、回收率是回收品质量水平的负指数函数，建立包含碳税成本(新产品和再制造品)在内的平均总成本模型，采用遗传算法(GA)、粒子群算法(PSO)验证模型的信度和效度。结果表明:企业可根据回收品的质量水平，合理安排再制造和制造批次来降低平均总成本;不同碳税水平下,合理的再制造和制造批次同样可降低总成本。该研究为企业在回收品不同质量水平下权衡碳排放因素降低总成本和政府制定合理的碳税政策提供参考。

回收品质量水平;多周期闭环混合系统;碳税;GAamp;PSO

环保意识、社会责任和立法制度日益成为推动企业回收再制造的关键因素[1-5]。各行业相继从事产品再制造活动并取得可观的经济效益,如地毯[6]、手机[7]、打印机墨盒[8]、轮胎[9]等。作为闭环供应链的重要组成部分,再制造可有效处理废旧品并具有提高生产率、节能减排、树立良好企业形象的巨大潜力[10]。

由于立法与经济因素的驱动,制造商也都积极参与产品回收再制造活动[11,12]。生产者责任延伸制度(EPR)作为一项环境政策,要求生产者对产品的整个生命周期负责,最大程度地减少环境污染[13]。且制造商熟悉产品和生产流程,可以同时兼顾制造、再制造活动,最大化整个供应链的利润[14]。再制造过程中,回收品质量的高度不确定性使闭环供应链的管理更加困难[15]。Behret等[16]将回收品质量分为三个等级,并与未分类的基准模型进行了对比,研究质量不确定的影响;Zeballo等[2]考虑回收品质量和数量的不确定性,用混合整数线性规划模型解决闭环供应链的网络规划问题;Cai等[17]将混合制造/再制造系统的回收品质量划分为两个等级,通过混合整数线性规划,研究最优回收价格和制造数量。

环境问题备受关注,政府为构建低碳经济发展模式,采用相关政策激励企业进行碳排放差异大的回收再制造[18]。作为一项有效的减排政策,碳税越来越受到学术界的重视[19]。常香云[20]基于碳税、补贴等不同政策,建立系统动力学模型,研究了环境政策对企业生产决策的影响;He等[21]基于最低碳排放量,建立成本最小化的物流网络设计模型,研究解决不确定环境下闭环物流网络设计的优化问题;Chaabane等[22]基于经济和环境目标,建立可持续发展的供应链优化模型,可为不同环境政策下的供应链优化问题提供决策依据。多数研究主要侧重于再制造的碳排放,本文则同时考虑混合制造/再制造系统的碳排放问题。由于再制造过程中碳排放量因回收品质量的不同而异,因此有必要考虑碳排放的差异化。

基于以上分析,本文假设回收率、再制造成本、回收成本受回收品质量水平的影响。在回收品不同质量水平的混合制造/再制造系统中,既要考虑制造品的碳税成本,又要根据回收品的不同质量水平考虑相应的碳税成本。研究多周期下回收品不同质量水平的最佳制造和再制造批次,可为企业的生产决策提供理论支持。同时,研究不同碳税下的最优运作策略与成本,可为政府设定碳税值提供参考依据。

1 模型构建

本文研究了原材料库存、回收品库存、可用库存三级库存的多周期闭环混合制造/再制造系统(图1),系统中需求由原材料制造和回收品再制造共同满足。

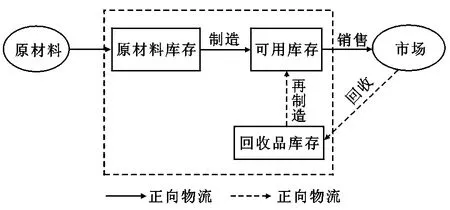
图1 混合制造/再制造系统

1.1 模型假设

主要是:①回收品质量水平服从正态分布,简化计算,本文假设服从标准正态分布[23]。②回收成本、再制造成本、回收率是关于回收品质量水平的负指数函数[24]。③回收品可全部用于再制造[25]。④再制造品和新产品具有相同的包装、价格,且质量无差异[26，27]。⑤不考虑提前期、缺货和过剩[28]。

1.2 函数构建

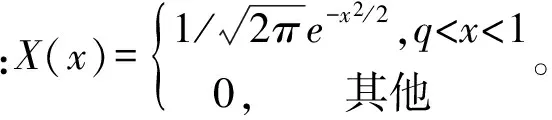
回收成本函数:回收成本是回收品质量水平的函数,p=ae-θ(I-x)[24](图2),其中0≤a≤1,参数a、θ根据不同情况进行调整[30]。回收成本比率p是单位回收品回收成本与单位新产品生产成本(单位制造成本Cn和单位原材料采购成本Craw)的比值。那么平均回收成本V1=d(Cn+Craw)E(p),其中:

即V1=abe-φq+(ϑ2-2ϑ)/2[φ(1-ϑ)-φ(q-ϑ)]D(Cn+Craw)

(1)

图2 回收成本比率p

再制造成本函数:再制造成本是回收品质量水平的函数,s=ceδ(1-x)[30](图3)。其中0≤c≤1,参数c、δ根据不同情况进行调整[29]。再制造成本比率s是单位再制造成本与单位制造成本cn的比值。平均再制造成本V2=dCnE(s),其中:

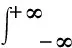
即V2=cbe-φq+(δ2+2δ)/2[φ(1+δ)-φ(q+δ)]DCn

(2)

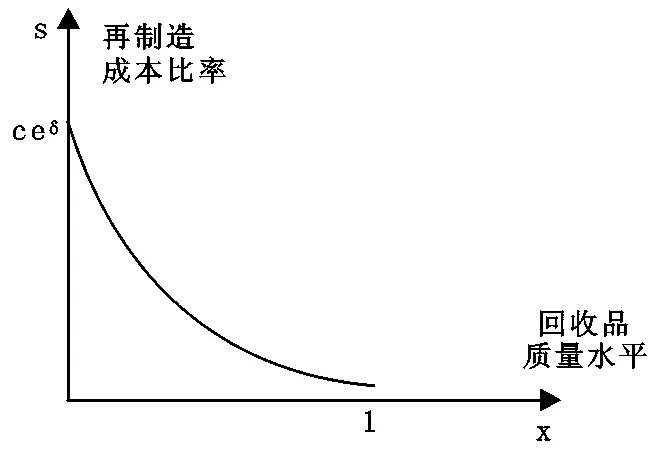
图3 再制造成本比率s

图4 物料流动

1.3 系统模型

库存水平:回收品、制造品和再制造品的数据与流向见图4。

对生命周期较短的回收品而言,价值随搁置时间递减[23]。因此,本模型考虑第一阶段回收品再制造,第二阶段新产品制造。第一阶段:再制造品库存以(1/γ-1)D的速率上升,同时回收品库存以(α-1/γ)D的速率下降。第二阶段:制造品库存以(1/β-1)D速率上升,同时回收品库存以αD的速率上升,原材料库存以(-1/β)D(制造率)的速率下降,见图5。计算可得:I1=(1-β)(1-α)DT/n、I2=(1-γ)αDT/m、I3=α[(1-α)+α(1-γ)/m]DT、I4=nDTn=(1-α)DT。

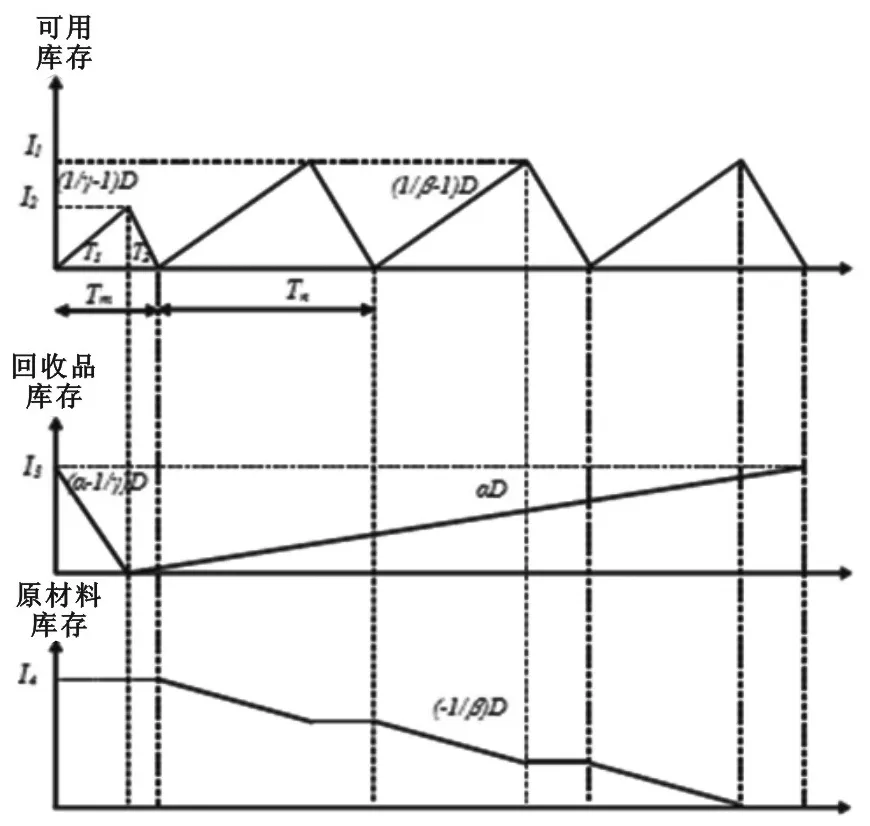
图5 库存水平(m=1,n=3)

平均库存持有成本:平均库存持有成本V3=制造品平均库存持有成本H1+再制造品平均库存持有成本H2+回收品库存持有成本H3+原材料平均库存持有成本H4:

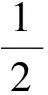
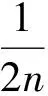
(3)

(4)

式中,C为单位碳排放的碳税成本,ex为单位再制造品碳排放,em为单位制造品碳排放。

平均制造成本:V5=(1-α)DCn

(5)

平均准备成本:V6=(nS1+mS2)/T

(6)

式中,S1为再制造准备成本;S2为制造准备成本。

平均原材料成本:V7=(1-α)DCraw

(7)

平均订购成本:V8=CO/T

(8)

式中,C0为订购成本。

将α=be-φq带入总成本函数,得:

ATC=(1)+(2)+(3)+(4)+(5)+(6)+(7)+(8)

(9)

2 算例分析

2.1 粒子群算法简介与过程

粒子群算法(PSO)是一种随机智能搜索算法,通过不断更新行动轨迹获得目标的最优解[31]，具有收敛速度快、优化质量高等特点[32]，因此本文采用粒子群算法求解多目标问题。

随机初始化M个粒子进行搜索,每个粒子代表一个解。假设粒子i经过T次迭代后的位置为Xi=(xi1,xi2,xi3,…,xin)T,速度为V1=(vi1,vi2,vi2,…,vin)T。将Xi带入目标函数(9)求出适应度值,即可知道粒子i的最优位置和所有粒子不断迭代后经历的最佳位置,分别用Pi=(pi1,pi2,pi3，…，pin)T和Pg=(pg1,pg2,pg3,…,pgn)T表示。式中,T为迭代次数。粒子在迭代中根据下列方程更新位置和速度:

(10)

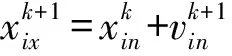
1≤i≤n;1≤n≤N

(11)

粒子群算法的主要编写步骤为:①设定粒子规模为M,随机初始化粒子的速度和位置、模型初始化周期T、制造次数n、再制造次数m。②根据目标函数(9)得到所有粒子的适应度值。③不断更新迭代粒子的速度和位置并比较,若当前适应度值大于自身最好的适应度值,则设置当前位置为Pbest。若本次迭代后,所有粒子中最优的适应度值大于先前最好的适应度值,则设置群体最优位置gbest。④根据方程(10)—(11)不断变化更新粒子位置和速度。⑤若粒子未到达最优适应度值,则转向步骤二,否则终止操作。

2.2 遗传算法简介与主要过程

遗传算法是一种模拟生物进化过程以随机搜索寻求最优解的算法,具有高效、鲁棒性强、全局优化、灵活等特点[33]。遗传算法的主要步骤为:①随机产生一组初始种群,用染色体编码代表各个体。②适应度评估与选择。利用目标函数(9)确定个体的适应度值,本文旨在寻求目标函数的最小值,因此值越小,适应度越高。根据适应度值决定是否被选择并作为父代,选择操作提高全局收敛性。③交叉与变异。交叉通过一定概率来获得新个体,保证全局搜索能力;变异是用等位基因代替串结构中某些基因,保证种群多样性及局部搜索能力。④终止规则。若到达预设的进化代数,则终止,否则转向步骤二。

表1 制造品和再制造品的单位碳排放量

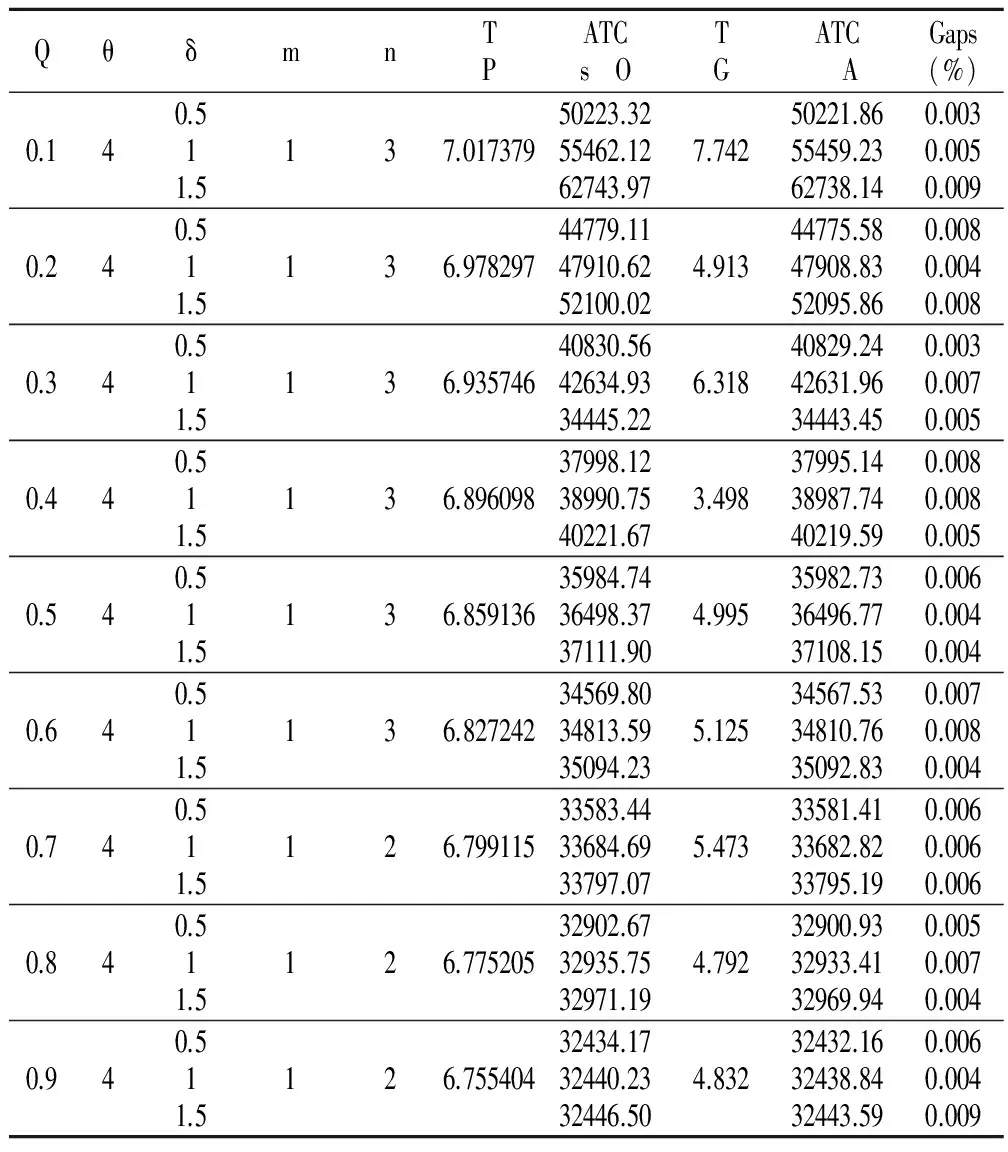
表2 最优运作策略(回收品不同质量水平)

2.3 计算结果

已知，hs=1、hr=0.2、hraw=0.2、Cn=20、Craw=10、CO=1000、S1=1500、S2=1500、D=1000、a=0.9、b=0.1、c=0.9、γ=0.1、β=0.9、φ=2,λ=1,参数是在以往研究的基础上整理得到[34]。针对回收品不同质量水平(0.1—0.9),单位碳排放量见表1。其中,数据参考相关文献[35]并经过整理得到;回收品不同质量水平的最优运作策略见表2,其中GAP值=(PSO-GA)/GA。不同碳税下不同质量水平的最优运作策略见表3,随回收品质量水平变化的平均总成本波动情况见图6。

表3 最优运作策略(不同碳税)

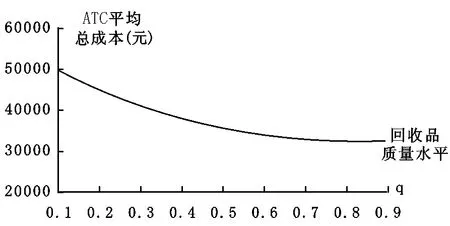
图6 回收品质量水平对平均总成本的影响

表2表明:①当回收品质量水平为0.1—0.9、通过参数值的带入时,两种算法都适用于模型求解,且GAP主要集中在0.003%—0.009%,验证了模型的有效性。两种算法的偏差表明不同条件下的解未陷入局部最优,验证了模型的可信性。②随着回收品质量水平的升高,再制造次数与制造次数比例(m:n)逐渐增大,本例中回收成本的增长幅度小于再制造成本的下降幅度,因此平均总成本降低。③在回收品同一质量水平下,企业的最优生产策略是合理规划再制造次数与制造次数比例,同时考虑碳排放总量来降低平均总成本。④随着δ的增大,ATC逐渐增大。即再制造成本上升引起平均总成本上升,因此企业的最优再制造策略是再制造满足最低再制造成本的产品(较高质量水平的回收品),从而降低再制造成本和总成本。⑤本例中当回收品质量水平为0.9、再制造次数与制造次数比例为1∶2时,平均总成本达到最小值。

表3是研究回收品在不同质量水平下,不同碳税对平均总成本的影响。研究结果显示:①随着碳税的增加,平均总成本逐渐上升,因此企业生产运作时应尽可能考虑碳排放总量,通过调整生产过程中再制造次数与制造次数的比例来降低总成本。②政府若想推动再制造,可考虑在回收品不同质量水平下合理增加碳税,从而提高再制造次数与制造次数的比例。其碳税成本增幅可借鉴模型中不同碳税下的最优平均总成本的差值。③在同一回收品质量水平下,提高碳税可直接提高企业再制造次数与制造次数比例和平均总成本。对政府设定的碳税值,企业可参考选择最优生产策略使平均总成本最小化。④企业的最优策略是根据模型中相应的回收品质量水平,结合政府相关政策来合理控制再制造次数和制造次数比例,以使平均总成本最低。⑤碳税值的设定需兼顾企业利益,只有追求经济利益和环保利益的平衡点,才能实现政府和企业的双赢。

图6表明:①随着回收品质量水平的升高,平均总成本逐渐降低。即企业愿意回收质量水平较高的产品，以确保自身的经济利益,而此时的回收率较低,因此政府可对回收质量水平较低的产品进行补贴,使企业在寻求经济利益的同时兼顾社会利益,加大较低质量水平产品的回收幅度,提高产品的回收率。②当回收品质量水平在0.1—0.2时,平均总成本的波动幅度相对较大,因此补贴额度过大。政府可对回收品质量水平在0.3—0.9时,采取合理的补贴措施促进企业回收进行再制造。

3 结论

本文研究了多周期制造/再制造系统在回收品不同质量水平与碳税下的最优运作模式。假设回收率、回收成本、再制造成本受回收品质量水平影响,其中回收品质量水平服从标准正态分布，通过算例并采用GA算法和PSO算法验证模型的信度和效度。企业在进行产品回收和生产时,可根据生产状况及相应的碳税政策合理安排生产回收策略，使平均总成本最小化。同时，政府可参考不同碳税值设定碳税政策,兼顾企业经济利益和社会利益来加大回收产品的再制造力度,其碳税成本增幅可借鉴模型中不同碳税下的最优平均总成本差值。

由于混合制造/再制造系统的复杂性,不确定因素随之增多,如市场需求、废弃率等，以及考虑产品缺货或剩余下的生产运作策略将是未来的研究方向。

[1]Giri B C,Sharma S.Optimal Production Policy for a Closed-loop Hybrid System with Uncertain Demand and Return Under Supply Disruption[J].Journal of Cleaner Production,2016,112(3)∶2015-2028.

[2]Zeballos L J,Gomes M I,Barbosa-Povoa A P,etal.Addressing the Uncertain Quality and Quantity of Returns in Closed-loop Supply Chains[J].Computers amp; Chemical Engineering,2012,47(12)∶237-247.

[3]Shi J,Zhang G,Sha J.Optimal Production and Pricing Policy for a Closed Loop System[J].Resources,Conservation and Recycling,2011,55(6)∶639-647.

[4]Rubio S,Corominas A.Optimal Manufacturing-remanufacturing Policies in a Lean Production Environment[J].Computers amp; Industrial Engineering,2008,55(1)∶234-242.

[5]Kovács G.Corporate Environmental Responsibility in the Supply Chain[J].Journal of Cleaner Production,2008,16(15)∶1571-1578.

[6]Bernon M,Cullen J.An Integrated Approach to Managing Reverse Logistics[J].International Journal of Logistics：Research and Applications,2007,10(1)∶41-56.

[7]Rathore P,Kota S,Chakrabarti A.Sustainability Through Remanufacturing in India：A Case Study on Mobile Handsets[J].Journal of Cleaner Production,2011,19(15)∶1709-1722.

[8]Francie K A,Jean-Pierre K,Pierre D,etal.Stochastic Models and Numerical Solutions for Manufacturing/Remanufacturing Systems with Applications to the Printer Cartridge Industry[J].Journal of Manufacturing Systems,2015,37(3)∶662-671.

[9]Muzenda E,Popa C.Waste Tyre Management in Gauteng,South Africa：Government,Industry and Community Perceptions[J].International Journal of Environmental Science and Development,2015,6(4)∶311-317.

[10]Li X,Li Y,Cai X.Remanufacturing and Pricing Decisions with Random Yield and Random Demand[J]. Computers amp; Operations Research,2015,54(C)∶195-203.

[11]Jung K S,Hwang H.Competition and Cooperation in a Remanufacturing System with Take-back Requirement [J].Journal of Intelligent Manufacturing,2011,22(3)∶427-433.

[12]张茹秀.基于再制造的闭环供应链产品协调模型[J].软科学,2014,(9)∶35-38,49.

[13]Johnson M R,McCarthy I P.Product Recovery Decisions Within the Context of Extended Producer Responsibility[J].Journal of Engineering and Tech-nology Management,2014,34(12)∶9-28.

[14]赵晓敏,朱贺,谈成薇.政府财政干预对OEM厂商绿色再制造的影响[J].软科学,2016,(6)∶30-34,56.

[15]Flapper S D P.On the Operational Logistic Aspects of Reuse[M].Developments in Logistics and Supply Chain Management.Palgrave Macmillan UK,2016∶279-287.

[16]Behret H,Korugan A.Performance Analysis of a Hybrid System Under Quality Impact of Returns[J].Computers amp; Industrial Engineering,2009,56(2)∶507-520.

[17]Cai X,Lai M,Li X,etal.Optimal Acquisition and Production Policy in a Hybrid Manufacturing/Remanufacturing System with Core Acquisition at Different Quality Levels[J].European Journal of Operational Research,2014,233(2)∶374-382.

[19]Chang X,Xia H,Zhu H,etal.Production Decisions in a Hybrid Manufacturing-remanufacturing System with Carbon Cap and Trade Mechanism[J].International Journal of Production Economics,2015,(162)∶160-173.

[19]杨王君,卢巍.低碳政策下多容量等级选址与配送问题研究[J].中国管理科学,2014,(5)∶51-60.

[20]常香云,钟永光,王艺璇,等.促进我国汽车零部件再制造的政府低碳引导政策研究——以汽车发动机再制造为例[J].系统工程理论与实践,2013,(11)∶2811-2821.

[21]He Q,Luo W.Low-carbon Closed-loop Logistics Network Design Based on Interval Number Multi-attribute Decision and Queuing Theory[J].Methodology,2014,7(3)∶235-248.

[22]Chaabane A,Ramudhin A,Paquet M.Design of Sustainable Supply Chains Under the Emission Trading Snufacturing[J].Computers amp; Industrial Engineering,2013,64(4)∶29-936.

[23]Shi J,Zhang G,Sha J.Optimal Production Planning for a Multi-Product closed Loop System with Uncertain Demand and Return[J].Computers amp; Operations Research,2011,38(3)∶641-650.

[24]Vørøs J.Product Balancing Under Conditions of Quality Inflation,Cost Pressures and Growth Strategies[J].European Journal of Operational Research,2002,141(1)∶153-166.

[25]Liang Y,Pokharel S,Lim G H.Pricing Used Products for Remanufacturing[J].European Journal of Operational Research,2009,193(2)∶390-395.

[26]易余胤,袁江.渠道冲突环境下的闭环供应链协调定价模型[J].管理科学学报,2012,(1)∶54-65.

[27]Aras N,Verter V,Boyaci T.Coordination and Priority Decisions in Hybrid Manufacturing / Remanufacturing Systems[J].Production and Operations Management,2006,15(4)∶528-543.

[28]Wang J,Zhao J,Wang X.Optimum Policy in Hybrid Manufacturing/Remanufacturing System[J].Computers amp; Industrial Engineering,2011,60(3)∶411-419.

[29]Sang H Y.A Closed Loop Recycling System with Minimum Allowed Quality Level on Returned Products[M].Daejeon：Korean Advantage Institute of Science and Technology,2008∶41-51.

[30]李新军.再制造成本随机分布和市场细分的生产优化模型[J].中国管理科学,2007,15(5)∶72-77.

[31]Hamta N,Ghomi S M T F,Jolai F,etal.A Hybrid PSO Algorithm for a Multi-objective Assembly Line Balancing Problem with Flexible Operation Times,Sequence-dependent Setup Times and Learning Effect[J].International Journal of Production Economics,2013,141(1)∶99-111.

[32]Gen M,Cheng R,Lin L.Network Models and Optimization：Multi-objective Genetic Algorithms Approach[M].Springer,London,2008∶710-719.

[33]Oreski S,Oreski G.Genetic Algorithm-based Heuristic for Feature Selection in Credit Risk Assessment[J].Expert Systems with Applications,2014,41(4)∶2052-2064.

[34]Guo J,Ya G.Optimal Strategies for Manufacturing/Remanufacturing System with the Consideration of Recycled Products[J].Computers amp; Industrial Engineering,2015,(89)∶226-234.

[35]Yang C H,Liu H,Ji P,etal.Optimal Acquisition and Remanufacturing Policies for Multi-product Remanufacturing Systems[J].Journal of Cleaner Production,2015,(135)∶1571-1579.

OptimalStrategiesofDifferentQualityLevelofReturnedProductsforManufacturing/RemanufacturingEnterprisesUnderCarbonTax

WANG Xin-yue,GUO Jian-quan

(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

Considering the circumstances of different quality level of returned products,optimal operation strategies of different carbon taxes were investigated for manufacturing/remanufacturing enterprises in a multi-period closed-loop hybrid manufacturing/remanufacturing system,where the demand was satisfied by manufacturing from raw materials as well as remanufacturing from returned items into as-new products.A model was developed to minimize the total cost of the system considering carbon emissions for manufacturing/remanufacturing products.It was assumed that the quality of returned products was set to be standard normal distribution.Buyback cost,remanufacturing cost and return rate were negative exponential function of quality level of returned items.A numerical example was used to verify the validity of the model by adopting Genetic Algorithm(GA) and Particle Swarm Optimization (PSO)algorithm.The results showed that the enterprises could arrange reasonably the number of remanufacturing and manufacturing frequency ratio of different quality level of returned products to minimize the total cost,the rational number of remanufacturing and manufacturing frequency ratio could reduce the total cost under different carbon taxes.A good reference could be provided for minimizing the total costs of the system under different quality level of returned products considering the carbon emission for enterprise as well as initiating a reasonable carbon tax policy through this research.

quality level of returned products;multi-period closed-loop hybrid system;carbon tax;GAamp;PSO

2016-11-14；

2016-12-23

国家自然科学基金资助项目(编号:71071093、71471110);陕西省社会科学基金资助项目(编号:2015D060)。

及通讯作者简介：王心月(1992-),女,河南省南阳人,硕士研究生,研究方向为物流工程。

X320.22

A

1005-8141(2017)01-0059-05