一类反应扩散捕食模型高维空间中的古典解

侯立春

（铜陵学院数学与计算机学院，安徽铜陵244000）

一类反应扩散捕食模型高维空间中的古典解

侯立春

（铜陵学院数学与计算机学院，安徽铜陵244000）

文章讨论的反应扩散捕食模型带有交错扩散项，目前有关此类模型的已知结果非常少，文章主要应用能量估计方法，并结合Shauder理论和Bootstrap技巧证明了模型高维空间中古典解的存在性.文章研究结果可视为具有交错扩散项的Lotka-Volterra竞争模型相关工作在一定程度上的推广.

捕食-食饵模型；交错扩散；古典解；能量估计

1 引言与主要结论

本文讨论如下带有交错扩散项的捕食-食饵模型

其中di,αii(i=1,2,3),α31,α32，均为正的常数.d1,d2,d3分别为三个种群的扩散率.αii(i=1,2,3)为自扩散率，表明个体从种群的高密度区向低密度区运动.α31,α32为交错扩散率，交错扩散表示一个种群向另外一个种群流动.一般地，交错扩散系数可以是正的、负的或者是零.正的交错扩散项表示一个种群向另一个种群的低密度区扩散，负的交错扩散项表示向另一个种群的高密度区扩散，交错扩散为零表示种群是自包含的，更具体的生物意义可参见文献[1].

为简单起见，在讨论过程中始终假定系数a0,a1,a2,a3,k,b为正常数，给定相关符号为

本文的主要结果是关于模型在高维空间中古典解的存在性，结论叙述如下：

定理1.1设初值u0,v0,w0≥0满足齐次Neumann边界条件，且u0,v0,w0∈C2+λ(Ω¯)(λ∈(0,1)).如果空间Ω的维数n＜6，则问题(1.1)有唯一非负古典解

2 辅助引理及证明

引理2.1设问题(1.1)解为(u1,u2,w).则存在正的常数，使得

证明对(1.1)应用比较原理[2]，易知.u1≥0,u2≥0,w≥0

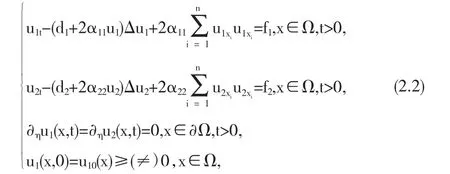
注意到f1,f2在R2上充分光滑，在R+2上拟单调.设(0,0)，(M,N)为辅助问题(2.2)的一对上、下解，其中M,N为正的常数.直接计算不等式

引理2.2设X=(d1+α11u1)u1，u∈L∞(QT)为下列方程的解

其中d1，α11为正常数，且0≤w≤L2(QT).则存在依赖于||u10||

进一步地，

证明由X=(d1+α11u1)u1，易知

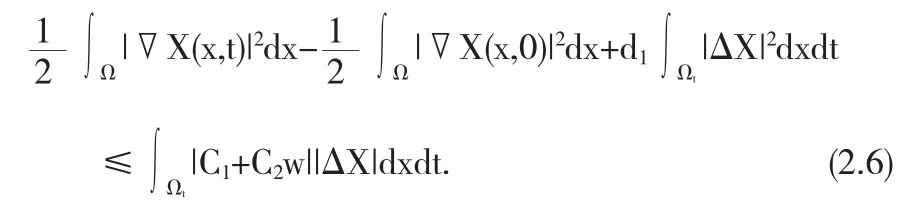
对(2.6)的右端使用Hölder不等式和Young不等式，对某个m1＞0，我们有

将(2.7)代入(2.6)，得到

其中m2依赖于方程的正则性估计([3,Lemma2.3]),得

引理2.3(引理2.3可综合文献[4]中引理2.3及引理2.4得到)

且存在β∈(0,1)和CT使得则存在依赖于n,Ω,p,β和CT的正常数M'，使得

引理2.4设Ω∈RN为有界区域且∂Ω⊂C2，则对∀u1∈

其中C是依赖于q,n,Ω,T的正常数.

3 主要结论的证明

下面分三步完成模型(1.1)非负古典解的存在性，即对定理1.1进行证明.

证明第一步，关于w的L1-,L2-及Lq-估计.首先，对(1.1)的第三个方程在Ω上积分，得

从而，

进一步地，

在[0,T]上对(2.8)积分，得

其次，在(1.1)的第三个方程两边乘以qwq-1(q＞1)，并在Ω上积分，得

上式在[0,T](t≤T)上积分，得

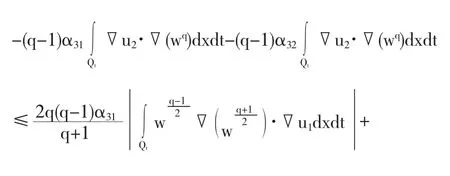
于是由引理2.3和(2.16)，得

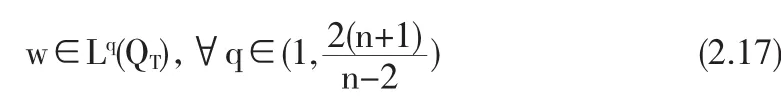
最后，不难看出q=2满足(n2-4)q＜n2+4n,(n=2,3,4,5).所以在(2.11)和(2.12)中取q=2，则存在正常数M4，使得

第二步，关于w的L∞-范数估计.将模型(1.1)的第三个方程改写为

(1)||w||V2(QT)有界

其中u2,μ1为正常数，q,r满足

下面依次证明条件(1)-(3)成立.由(2.18)，并注意到n≤5，易知条件(1)成立.只须选取u2=d3，则条件(2)成立.为了证明条件(3)，将(1.1)的第一个方程改写为

由引理2.1，d1+2α11在QT上有界.对任意对(2.21)，由Hölder连续性([5,T h10.1,p.204]),得

返回到(2.5).由(2.1)和(2.17)知，C1+C2w∈Lq(QT),∀q∈从而对(2.5)，由抛物方程的正则性([13,T h9.1,p.341-342]),得

第三歩，证明对于任意T＞0,模型(1.1)的解(u1,u2,w)在QT上是古典的.因为(d1+2α11u1)f1对任意q＞1，由(2.24)有所以，对∀β*∈(0,1),从而由Lemma3.3([5],又通过直接计算X=(d1+α11u1)u1，得

将(1.1)的第三个方程重写为

综合上面证明的系列结果，易知(-b+u1-w)w∈L∞(QT)且u1,u2,w,▽u1,▽u2在QT上有界.于是由Theorem10.1([5],p.204)知，存在σ1∈(0,1)，使得

类似于引理2.2的证明，我们有▽u2∈L2(QT),即u2∈V2(QT),则对(1.1)的第二个方程应用Theorem10.1，存在σ2∈(0,1),使得

进而应用Schauder估计([5],p.320-321)，对σ*=min{σ2,λ}有由Sobolev嵌入定理，则同样使用Schauder估计，可得

其中f(x,t)=(d3+a31u1+a32u2+2a33w)(-b+u1-w)w+(a31u1t+a32u2t)w由(2.25)-(2.27),我们有(2.29)应用Schauder估计，可得

将(1.1)的第一个方程改写为

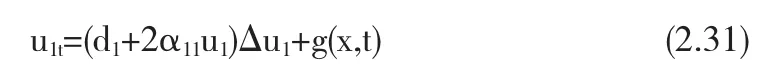
特别地，如果λ＜α，则σ=λ，即定理2.1被证明.如果α＜λ，由Sobolev嵌入定理知重复上述Bootstrap技巧和S hauder估计过程，定理2.1的证明被完成.

〔1〕B.Dubey,B.Hussain,A predator-prey interaction model with self and cross-diffusion,Ecological Modelling.141(2001)67-76.

〔2〕M.H.Protter,H.F.W einberger,Maximum Principles in Differentical Equations,2nd ed,Spring-Verlag,New York,1984.

〔3〕Y.Lou,W.N i,Y.W u,On the global existence of a cross-diffusion system,Discreate and Continuous Dynamical Systems.4(1998)193-203.

〔4〕Y.S.Choi,Roger Lui,Yoshio Yamada.Existence of Global Solutions for the Shigesada-Kawasaki-Teramoto Model with Strongly Coupeled Cross-diffusion,Discreate and Continuous Dynam ical Systems.10(2004)719-730.

〔5〕O.A.Ladyzenskaja,V.A.Solonnikov,N.N.Uralceva,Linear and Quasilinear Partial Differential Equations of Parabolic Type,Translations of Mathematical Monographs,23,AMS,1968.

〔6〕谢君辉，刘婷婷，等.一类具反应扩散的捕食模型平衡态模式的定性分析[J].湖北民族学院学报(自然科学版)，2015（03）.

O175.26

A

1673-260X（2017）11-0003-04

2017-08-18

安徽省高校自然科学研究重点项目(KJ2015A251)；池州学院自然科学研究项目（2016ZR009）