积分学教学方法的探讨
牛艳秋
(吉林建筑大学城建学院,吉林长春130111)
积分学教学方法的探讨
牛艳秋
(吉林建筑大学城建学院,吉林长春130111)
本文主要阐述了在教学中如何更好地应用元素法思想来求解定积分、重积分问题,以及怎样推广元素法,并结合“元素法”的思想,得出三重积分的计算公式.
元素法;定积分;截面法;投影法
1 关于分部积分法的教学
2 在定积分概念教学中渗透元素法思想
元素法是定积分应用中的基本思想方法,是解各类应用题的法宝.一般教材中通常在介绍定积分应用时才涉及元素法,在教学实践中,我体会到可以将“元素法”提前在定积分概念教学中“渗透”.具体讲授时,在讲完分割、近似、求和、取极限引出定积分的概念后加以说明:若在“近似”阶段,为简便计算,省略下标i,把这一区间记为[x,x+dx],取ξ为x,则相应的窄曲边梯形面积近似为ΔA≈f(x)dx,且当λ→0时,dx→0,这样的窄曲边梯形有无数个,整个曲边梯形可视为这无数个窄条矩形(形象上为无数条直线段)构成,这些窄条矩形面积即是构成曲边梯形面积的“元素”.一旦元素f(x)dx找到了,则将这无穷多个元素累加,即可得所求曲边梯形面积.这样讲授自然流畅,即使学生对“元素”有了比较直观的感性认知,又为后续应用“元素法”埋下伏笔,指明了基本思想方法,即欲求某个量,就要设法找出其“元素”,然后将这无穷多个元素累加(积分)即得所求量.另外,这种“元素法”的思想方法也对理解重积分的计算方法提供了帮助(见下目).
3 多元积分学教学中引入具体模型
二重积分是以求曲顶柱体体积和平面薄片的质量这两个具体模型引入的,而三重积分及第一类曲面积分,则通常是直接引入定义.在教学实践中如果也对它们赋予具体的物理模型,则对学生接受理解相关概念与算法是很有好处的.以三重积分为例,以求空间立体Ω的质量为引例导入,设f(x,y,z)为相应的体密度,经过分割、近似、求和、取极限步学生对三重积分有了感性的认知,同时也便于理解相关的性质.
另外,从这个具体的模型(空间立体的质量)出发,结合“元素法”的思想,可较方便地得出和理解三重积分的两种计算方法.
(1)投影法:设Ω:z1(x,y)≤z≤z2(x,y),(x,y)∈Dxy(图1),Dxy为Ω在xy面上的投影.将Dxy分成n个小区域,以dσ=dxdy为其任一小区域,(x,y)∈dσ,作以边界dσ为准线,母线平行于轴的柱面,它被z=z1可视其为立体Ω的质量“元素”,整个立体由无数个小柱状体构成,将这无数个“元素”累加,从而其质量为m=即得投影法计算三重积分的公式:

图1

图2

(2)截面法:设Ω:c≤z≤d,(x,y)∈Dz,(图2)Dz为竖坐标为的平面与Ω所截得的平面区域.将[c,d]分成n个小区间,以[z,z+dz]为其任一小区间,相应薄片的质量应为时,可视其为立体Ω的质量“元素”,整个立体由无数个小薄片构成,将这无数个“元素”累加,从而其质量为即得截面法计算三重积分的公式:
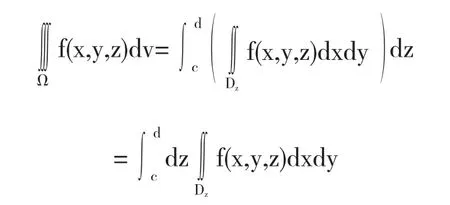
〔1〕徐兵.高等数学[M].北京:高等教育出版社,2010.8.
〔2〕春玲.强s-凸函数的simpson型积分不等式[J].内蒙古民族大学学报(自然科学版),2015(06).
O172.2
A
1673-260X(2017)11-0017-02
2017-08-17

