应用SOFxLMS算法的振动主动控制MATLAB仿真

孙文豪， 张锋， 汪涵， 罗顺安， 李海燕

(华侨大学 机电及自动化学院， 福建 厦门 361021)

应用SOFxLMS算法的振动主动控制MATLAB仿真

孙文豪， 张锋， 汪涵， 罗顺安， 李海燕

(华侨大学 机电及自动化学院， 福建 厦门 361021)

为了改进振动主动控制中控制算法的性能和提高对振动的控制效果，以滤波-x型最小均方(FxLMS)算法为基础改进得到SOFxLMS算法.在MATLAB/SIMULINK中利用level-2 S-函数搭建算法的自定义模块和仿真结构框图，在保证系统稳定及相同条件下分别对两种算法进行仿真对比.结果表明：改进后的SOFxLMS算法有效，且具有更好的收敛性能；在振动主动控制中滤波器阶数较少、迭代步长较大的情况下具有更好的控制效果.

振动主动控制； SOFxLMS算法； FxLMS算法； 次级通道； 脉冲响应系数； MATLAB仿真

振动主动控制是根据传感器获得的振动信号，通过作动器产生一个与振源大小相等、相位相反的振动信号来抵消有害振动[1].由于主动控制具有适应性强，控制效果好，计算复杂度低，能弥足被动控制技术的不足等优点，成为近年来振动控制工程领域的热点[2].控制算法是振动主动控制器的核心部分，而FxLMS(filtered-x least mean square)算法稳定性好，能够根据具体实际情况进行适应调整，被应用于时不变系统，是振动控制领域应用最广泛的算法之一[3-4].目前,对FxLMS算法的研究多侧重于其自身特性及改进结构后在控制系统中应用.Qiu等[5]分析时域中影响单输入单输出FxLMS算法控制输出的3个因素，提出了相应的解决方案.Chang等[6]提出一种基于神经网络的FxLMS算法来抵消非线性宽频带噪声.Tang等[7]针对短暂的傅里叶变换的主动噪声控制研究提出一种时频域FxLMS算法，与时域FxLMS算法相比，此算法拥有更好的收敛性能和较低的计算复杂度.李以农等[8]针对齿轮传动系统振动主动控制，提出一种次级通道在线辨识的反馈FxLMS算法.Bo等[9]针对窄频带主动噪声控制提出一种累积加权FxLMS算法，通过将动量LMS算法应用到FxLMS算法中改进得来.Song等[10]针对主动噪声控制应用了一种基于FxLMS算法修正的可优化变步长的仿射投影算法.以上诸多针对提升算法收敛速度和降低稳态误差的研究虽在一定程度上达到了预期效果，但往往增加了算法在结构和计算上的复杂度.本文基于对FxLMS算法的分析，提出应用一种改进的SOFxLMS(self-orthogonalizing filtered-x least mean square)算法，并将SOFxLMS算法与FxLMS算法分别应用到振动主动控制的仿真研究中，对算法的整体性能和振动控制效果进行对比分析及验证.

图1 FxLMS算法结构框图Fig.1 FxLMS algorithm structure

1 SOFxLMS算法结构

FxLMS算法的结构框图,如图1所示.在FxLMS算法中，首先,参考信号X(n)经过初级通道滤波延迟后得到初始振动信号；同时，参考信号X(n)经模拟次级通道的模型后得到滤波后的输入信号XS(n)；然后，XS(n)与误差信号e(n)的乘积作为误差梯度的估计值参与到算法的权值迭代过程之中.

误差信号e(n)为初始振动信号d(n)与控制器输出的反振动信号YS(n)之和，即e(n)=d(n)-YS(n)；N阶FIR滤波器的输出Y(n)等于卷积运算，有

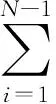
在仿真中，次级通道传递函数在时域内可以用m阶FIR滤波器来建模，即S=[S0，S1，…，Sm-1]；而滤波后的输入信号则为

控制器产生的控制信号等于滤波器与次级通道传递函数的卷积，即YS(n)=Y(n)S.

次级通道主要包括D/A转换器、功率放大器、作动器、物理通道、误差传感器及其他成分.当参考信号通过次级通道滤波后，输入信号的自相关矩阵就不再对角化，且矩阵的特征值扩散度就会增大，算法的收敛速度就会降低[11].当次级通道的脉冲响应系数可知，就可利用其相关元素使滤波后输入信号的自相关矩阵对角化，并将输入信号的自相关矩阵的变形应用到算法的权值迭代更新公式中，从而得到改进后的SOFxLMS算法.因此，SOFxLMS算法是FxLMS算法运用一种数学的方法改进得来，故SOFxLMS算法的结构与FxLMS算法无异.SOFxLMS算法的权值迭代公式为

图2 SOFxLMS算法程序流程图Fig.2 Flow chart of SOFxLMS algorithm

式(3)为SOFxLMS算法的权值迭代推导公式，在实际算法中,可按照以上公式设计算法的程序.SOFXLMS算法程序流程图，如图2所示.

2 SOFxLMS和FxLMS算法模块的建立

MATLAB/Simulink中的信号处理工具箱可进行数字信号处理系统设计仿真及分析.由于level-1 S-函数无法处理复数数据及基于帧的数据，故采用SIMULINK中的level-2 S-函数.分别自定义SOFxLMS和FxLMS控制算法模块，采用M语言编写算法程序.

文中利用主要的函数体完成基于level-2 S-函数的SOFxLMS和FxLMS控制算法模块.在建立SOFxLMS和FxLMS算法模块时主要应用以下回调方法.

1) 用Setup函数体进行模块的初始化工作，而在构建算法模块时必须用到Setup函数体来执行以下3类任务：① 设置参考信号，即滤波后输入信号和误差信号3个输入端口，以及权值迭代系数和控制信号两个输出端口；② 设置端口的属性，即维数、复杂度、数据类型及采样时间；③ 设置对话参数并检验参数的有效性.

2) 用CheckPrms函数体检验算法步长μ值的合法性，如果对话参数超出自定义范围，则程序进行报错指示.

3) 设置变量的初始属性.为了进行数据的及时更新，用DoPostPropSetup函数体建立两个Dwork向量，分别为参考信号迭代向量X(n)和权值迭代向量ω.当搭建的 S-函数模块被多次调用，则必须采用Dwork向量，而不能采用全局或静态变量.

4) 用Start函数体设置Dwork向量的初值为0.

5) 用Outputs函数体将SOFxLMS和FxLMS算法的权值迭代,以及更新滤波器参数的计算结果送至输出端.

3 算法实现及仿真验证

为了对自建的SOFxLMS和FxLMS两种算法模块进行验证，按照模块化建模的思想[12]，在SIMULINK中分别搭建基于以上两种算法的振动主动控制的仿真结构，如图3，4所示.

分别取激励源为100,110,120 Hz，且幅值均为1的3个正弦信号和随机信号叠加后作为模拟的初始振动信号;初级通道和次级通道均采用FIR滤波器，控制滤波器阶数N分别设定为50,80及110;算法步长μ分别设为0.010 0,0.001 0及0.000 1，采样时间为0.000 1 s，仿真时间为10 s.

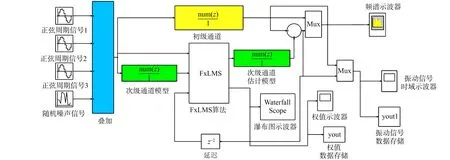
图3 FxLMS算法仿真结构框图Fig.3 Simulation structure of FxLMS algorithms

图4 SOFxLMS算法仿真结构框图Fig.4 Simulation structure of SOFxLMS algorithms

在保证系统稳定和其他基本条件相同的前提下，对两种算法采用相同控制滤波器阶数，不同的迭代步长进行3组仿真研究，并通过对比分析两种算法的收敛性能和振动主动控制效果.设定初级通道传递函数P(z)及次级通道传递函数S(z)[2]分别为

3.1算法的权值迭代图和时域控制效果图

当滤波器阶数N分别为50，80,100时，两种算法的权值收敛和振动时域控制效果图，分别如图5～7所示.图5～7中：ω为权值；A为振幅；t为仿真时间.

由图5可知：当两种算法在滤波器阶数N=50时的条件下，SOFxLMS算法在步长μ=0.001时开始收敛，算法在时域内表现出良好的控制效果；而FxLMS算法始终发散，并没有产生控制效果.

由图6可知：当两种算法滤波器阶数增加至N=80时，SOFxLMS算法在步长达到0.001时开始收敛，表现出良好的振动控制效果；而FxLMS算法的迭代步长减小至μ=0.000 1时，仍旧无法收敛，但有呈现出欲收敛的态势，也表现出一定的控制效果.

由图7可知：当滤波器阶数继续增至N=110时，SOFxLMS算法依旧在μ=0.001时开始收敛，而FxLMS算法在μ=0.000 1时也开始收敛，而且两种算法的控制效果也都较为明显.

由图5,6,7的(a),(c)可知:当算法滤波器阶数N一定时，减小算法的迭代步长，FxLMS算法未开始收敛时，SOFxLMS算法已经开始收敛，所以SOFxLMS算法整体上要比FxLMS算法表现出更出色的收敛性能.另外，不难发现当算法的迭代步长减小到一定时，增加滤波器阶数，两种算法最终都表现为收敛.当算法的迭代步长达到μ=0.000 1时，滤波器阶数从N=50逐渐增加至N=110时，两种算法都开始收敛.由图5，6，7的(b)，(d)可知：SOFxLMS算法在收敛的同时也表现出良好的控制效果和控制稳定性.

(a) SOFxLMS算法权值迭代(μ=0.001) (b) SOFxLMS算法时域控制(μ=0.001)

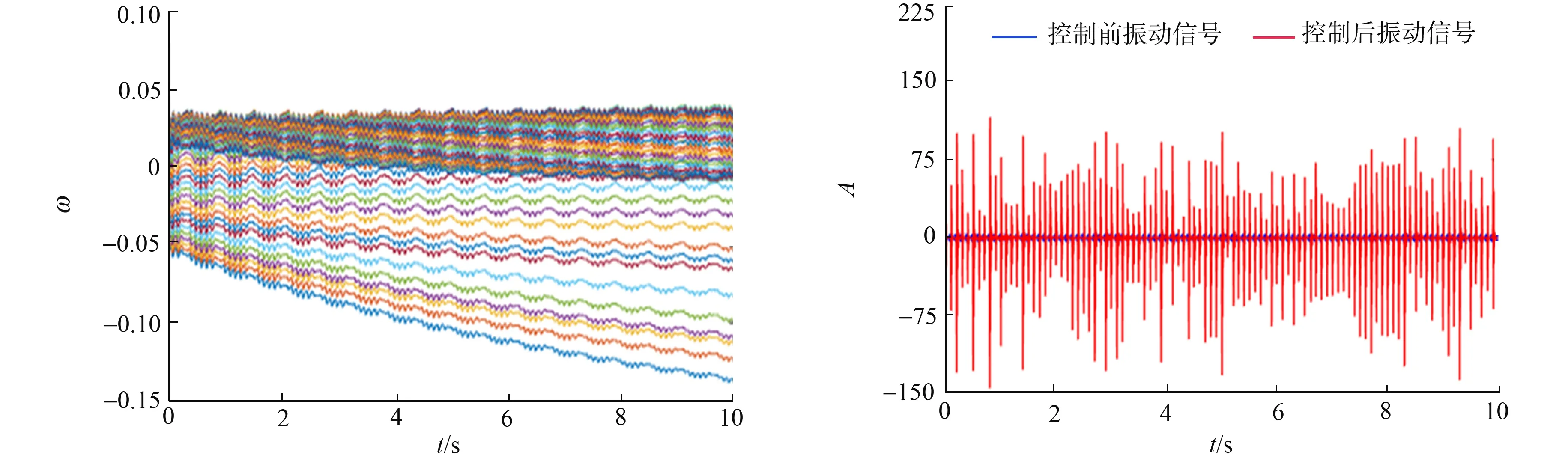
(c) FxLMS算法权值迭代(μ=0.000 1) (d) FxLMS算法时域控制(μ=0.000 1)图5 两种算法权值收敛和振动时域控制效果图(N=50)Fig.5 Two algorithm convergence curve of weight and active vibration control effect (N=50)

(a) SOFxLMS算法权值迭代(μ=0.001) (b) SOFxLMS算法时域控制(μ=0.001)

(c) FxLMS算法权值迭代(μ=0.000 1) (d) FxLMS算法时域控制(μ=0.000 1)图6 两种算法的权值收敛图和振动时域控制效果图(N=80)Fig.6 Two algorithm convergence curve of weight and active vibration control effect (N=80)

通过分析两种算法的权值迭代图和振动时域控制效果图，可以发现FxLMS算法在滤波器阶数相对较多和迭代步长较小的条件下收敛效果要优于SOFxLMS算法，控制效果也较好，如图7(d)，(e)所示.当滤波器阶数逐渐减少，同时迭代步长增大，FxLMS算法的性能明显不如SOFxLMS算法，而且最终控制效果也明显劣于后者.

(a) SOFxLMS算法权值迭代(μ=0.001) (b) SOFxLMS算法时域控制(μ=0.001)

(c) FxLMS算法权值迭代(μ=0.000 1) (d) FxLMS算法时域控制 (μ=0.000 1)

(e) SOFxLMS算法时域控制(μ=0.000 1)图7 两种算法的权值收敛和振动时域控制效果图(N=110)Fig.7 Two algorithm convergence curve of weight and active vibration control effect (N=110)

纵观图5～7可知：在滤波器阶数由少变多的大范围内，SOFxLMS算法的收敛性能和收敛速度较FxLMS算法有明显优越性.综合整体性能考虑，改进后SOFxLMS算法相对FxLMS算法在振动主动控制的研究中具有一定的进步和优势.

3.2算法的频域控制效果图

虽然通过时域控制效果图可以明显看出两种算法的控制效果，但为了进一步证明两种算法的有效性和在初始振动信号对应频率(f)所产生的控制效果，文中列举一组对比图进行分析证明.在滤波器阶数N=110，迭代步长μ=0.000 1时,根据图7(d)，(e)进行傅里叶变换得到两种算法在振动频域内的控制效果图，分别如图8(a)，(b)所示.图8中：S(x)为功率谱密度;f为频率.

(a) FxLMS算法 (b) SOFxLMS算法 图8 两种算法的频域控制效果(N=110，μ=0.000 1)Fig.8 Two algorithm control effect in frequency domain (N=110， μ=0.000 1)

由图8(a)，(b)对比可知：两种算法在目标频率处都有明显的控制效果，但FxLMS算法要较好于SOFxLMS算法，这说明FxLMS算法只在阶数较多、步长较小的良好条件下控制效果要强于SOFxLMS算法，但并不影响改进后的SOFxLMS算法的整体性能和对振动的控制效果.

4 结论

以FxLMS算法为基础改进得到SOFxLMS算法，通过改变次级通道脉冲响应系数，从而降低次级通道的影响和提高滤波x型最小均方(FxLMS)算法的收敛速度.利用MATLAB/SIMULINK中相应的模块搭建控制结构，对以上两种算法的控制性能进行分析和验证，得到以下3点主要结论.

1) 将改进后的SOFxLMS算法应用到振动主动控制仿真研究中，利用次级通道脉冲响应系数的元素使输入信号的自相关矩阵对角化，降低了次级通道对参考信号的影响.仿真结果证明了改进的SOFxLMS算法的正确性及实效性.

2) 仿真结果表明，当算法的调节参数在一定范围内，改进后的SOFxLMS算法较FxLMS算法在收敛速度和振动控制效果等方面得到明显的提高和改善，且参考信号的主要频率成分也得到有效抑制.

3) 当控制算法的滤波器阶数逐渐增大，计算复杂度增加，迭代步长逐渐减小，算法整体上收敛速度变慢，FxLMS算法比SOFxLMS算法逐渐表现出更好的控制效果和收敛稳定性.

[1] 张志谊，王俊芳，周建鹏，等.基于跟踪滤波的自适应振动控制[J].振动与冲击，2009，28(2):64-67.DOI:10.3969/j.issn.1000-3835.2009.02.016.

[2] 杨铁军，顾仲权，鲁明月，等.基于误差通道在线辨识的结构振动主动控制系统[J].振动与冲击，2004，23(3):55-59.DOI:10.3969/j.issn.1000-3835.2004.03.015.

[3] 张锋，李以农，丁庆中.FxLMS算法的实现及硬件在环仿真验证[J].重庆大学学报，2013，36(8):26-32.DOI:10.11835/j.issn.1000-582X.2013.08.005.

[4] 李元杰，戴再平.一种改进的MNVS自适应滤波算法[J].华侨大学学报(自然科学版)，2000，21(4)：404-407.DOI:10.3969/j.issn.1000-5013.2000.04.016.

[5] QIU X，HANSEN C H.An Algorithm for active control of transformer noise with on-line cancellation path modelling based on the perturbation method[J].Journal of Sound and Vibration，2001，240(4):647-665.DOI:10.1006/jsvi.2000.3256.

[6] CHANG Chengyuan，LUOH F.Enhancement of active noise control using neural-based filtered-x algorithm[J].Journal of Sound and Vibration，2007，305(1/2):348-356.DOI: 10.1016/j.jsv.2007.04.007.

[7] TANG X L，LEE C M.Time-frequency-domain filtered-x LMS algorithm for active noise control[J].Journal of Sound and Vibration，2012，331(23):5002-5011.DOI:10.1016/j.jsv.2012.07.009.

[8] 李以农，张锋，王雷,等.次级通道在线辨识的齿轮啮合振动主动控制[J].振动与冲击，2013，32(16):7-12.DOI:10.3969/j.issn.1000-3835.2013.16.002.

[9] BO Zhong，SUN Chao,XU Yonghui，etal.A variable momentum factor filtered-x weighted accumulated LMS algorithm for narrowband active noise control system[J].Measurement，2014，48(2):282-291.DOI:10.1016/j.measurement.2013.11.010.

[10] SONG J M，PARK P G.An optimal variable step-size affine projection algorithm for the modified filtered-x active noise control[J].Signal Processing，2015，114:100-111.DOI:10.1016/j.sigpro.2015.02.005.

[11] KRSTAJIC B，ZECEVIC Z，USKOKOVIC Z.Increasing convergence speed of FxLMS algorithm in white noise environment[J].AEU-International Journal of Electronics and Communications，2013，67(10):848-853.DOI:10.1016/j.aeue.2013.04.012.

[12] 王兵树，姜萍，林永君，等.SIMULINK中自抗扰控制技术自定义模块库的创建[J].系统仿真学报，2010，22(3):610-615.DOI：10.16182/j.cnki.joss.2010.03.037.

(责任编辑： 陈志贤英文审校： 崔长彩)

MATLABSimulationofActiveVibrationControlUsingSOFxLMSAlgorithm

SUN Wenhao， ZHANG Feng， WANG Han， LUO Shunan， LI Haiyan

(College of Mechanical Engineering and Automation， Huaqiao University， Xiamen 361021， China)

In order to improve the performance of the control algorithm in active vibration control, an improved algorithm SOFxLMS was obtained based on the filtered-x least mean square (FxLMS) algorithm. The level-2 S-function was utilized to set up the custom blocks of the algorithms and the block-diagram of simulation in MATLAB/SIMULINK. Two algorithms are simulated and compared under the conditions of ensuring the system stability and the same conditions. The results verified that the improved SOFxLMS algorithm is effective and has better convergence performance, and it has the better control effect under the conditions with lower order and larger iteration step size.

active vibration control； SOFxLMS algorithm； FxLMS algorithm； secondary channel； impulse response coefficient； MATLAB simulation

10.11830/ISSN.1000-5013.201611025

TB 535

A

1000-5013(2017)06-0779-07

2016-11-18

张锋(1979-)，男，讲师，博士，主要从事从事齿轮动力学、振动主动控制、压电智能材料等的研究.E-mail:alwaysqing@126.com.

国家自然科学基金资助项目(51405169)； 福建省自然科学基金面上资助项目(2015J01636)