利用奇异值分解的二阶递归系统数值稳定性方法

付波， 刘济源， 赵熙临， 徐光辉, 王子鹏

(湖北工业大学 电气与电子工程学院， 湖北 武汉 430068)

利用奇异值分解的二阶递归系统数值稳定性方法

付波， 刘济源， 赵熙临， 徐光辉, 王子鹏

(湖北工业大学 电气与电子工程学院， 湖北 武汉 430068)

为了简便地解决二阶递归系统的稳定性问题，将二阶递归系统转变为二阶离散时变线性系统，并讨论递归系统的稳定性.在二阶离散线性时变系统稳定性分析的基础上，利用奇异值分解(SVD)，将其转化为参考信号(RS)系统.提出一个新的离散时变线性系统不稳定性的充分条件，并以离散正交Krawtchouk多项式与Jacobsthal数列递归式为主，讨论并推导出其在Ⅱ,Ⅳ象限上的变化情况和新的不稳定性判据.仿真结果验证了结论的准确性.

Krawtchouk多项式； Jacobsthal数列; 奇异值分解； 递归系统； 线性离散时变系统

递归是一种利用简单操作实现复杂运算的有效方法，即通过简单的问题来解决复杂的问题[1].其表现形式较典型的是二阶递归，即数列的某一项是由其前两项计算所得[2-3].Legendre多项式、Chebyshev多项式、Jacobi多项式、Hermite多项式、Tchebichef多项式和Krawtchouk多项式等经典正交多项式[4-6]在图像正交矩、曲线拟合、非线性电路计算，以及计算结构可靠性分析等技术都有应用[7-8].但由于正交多项式解析式过于复杂，所以在实际应用中一般采用其递归式求解多项式的值.Mukundan等[9]发现正交多项式的二阶递归运算有可能导致数值发散，Gautschi[10-11]讨论了离散正交多项式的递归收敛性，关轶峰等[12]针对二阶离散线性时变系统的稳定性也做了大量研究.由于离散多项式不存在离散误差，其精度与高阶数值的传递有关，随着阶数的增大，多项式的数值和误差的增大更导致其不稳定，从而影响图像重构的精确性.Mukundan[13]利用x循环代替了n循环，同时，在一定程度上找到了高阶多项式的误差传递，解决了多项式高精度的算法问题.张海艳等[14]在图像分割、重构的问题上利用算法的稳定性，提出了概率密度函数在生物信息学上的研究.本文在二阶离散线性时变系统稳定性分析的基础上，利用奇异值分解(singular value decomposition,SVD)方法将其转化为参考信号(reference signal,RS)系统，提出一个新的离散时变线性系统不稳定性的充分条件，并通过实验验证其结果.

1 递归系统数值稳定性

1.1稳定性定义

(a) 稳定 (b) 不稳定图1 递归系统的稳定性状态Fig.1 Stability states of recursive systems

设系统初始状态x0位于以平衡状态xe为球心，半径为ε的球域H(ε)内.如果对所考虑的整个时间区间内，从H(ε)内任一点x0出发的受扰运动φ(t，x0，xe)的轨迹都不超出H(ε)，则称xe=0在李雅普诺夫下稳定，如图1(a)所示.对某个εgt;0，在所有半径为τ的球域H(τ)内的初始状态，至少存在一个初始状态，使得从它出发的解始终不会限制在以ε为半径的球域H(ε)里，则称平衡点在t0是不稳定的，如图1(b)所示.

1.2正交多项式

在矩函数集合中，分为连续正交多项式与离散正交多项式.Krawtchouk多项式是一种常见的离散正交多项式，更适合于对数字图像的处理.n阶Krawtchouk多项式的定义为

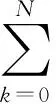
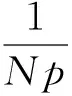
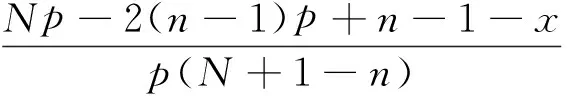
2 二阶递归系统的SVD模型

2.1SVD方法

设2×2矩阵G∈C2×2，C为复数集，RankG=2，则存在2阶酉矩阵U和2阶酉矩阵V，使得

式(3)中：Σ=diag(σ1,σ2)，且σ1≥σ2≥0，而σi(i=1，2，)为矩阵G的正奇异值.

对状态矩阵G(t)做SVD分解，可得G(t)=U(t)S(t)V(t)T.将U(t)，V(t)设定为单位旋转矩阵，又因为X(t)=G(t)X(t-1)，则有

将式(4)展开可得

重新定义Y(t)=X(t)，R(t)=U(t)及R(t-1)=[V(t)TU(t-1)]，Y(1)=V(1)TX(1)，可得

令D(t)=R(t)S(t)，则式(6)改写为

2.2RS系统的Ⅱ，Ⅳ象限稳定性分析

2.2.1 Ⅱ，Ⅳ象限状态变化 对于一个二阶离散线性系统

在第Ⅱ象限的初始相量，当σ1(k)gt;σ2(k),σ2(k)lt;1，σ1(k)gt;1，且π/2lt;θ(k)lt;π，初始点位于Ⅱ象限时，建立一个点经过一次RS变换后，角度与其反向角度的差值运动方程为

令f(κ(k))=0，可得

由此，特征根方程为

若能得斜率κ(k)经一个R(k)S(k)变化后，斜率为κ(k+1)且位于第Ⅳ象限的(-∞，κ*(k+1))之间;而经一次R(k+1)S(k+1)变化后，斜率为κ(k+2)且位于第Ⅱ象限的(-∞，κ1(k+2))之间，即

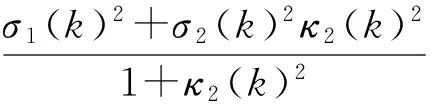
则可得该RS系统是不稳定的.

3 实验验证

3.1Krawtchouk多项式递归式稳定性分析

Krawtchouk多项式的三项递归迭代公式为

在x=390，p=0.1，0.3，0.9情况下，将Krawtchouk多项式整理为离散线性时变系统，其状态矩阵分解为两个旋转矩阵和一个斜变换，经SVD分解后可得:

图2 Krawtchouk的RS系统在Ⅱ，Ⅳ象限跳变发散情况Fig.2 RS Krawtchouk system jumps in Ⅱ,Ⅳ quadrants

2) 对角阵S(k)的主对角线参数σ1(k)，σ2(k);

RS系统在Ⅱ，Ⅳ象限跳变发散，如图2所示.各个SVD分解后的数值，如图3所示.

(a) θ(k)的范围 (b) 奇异值σ2(k) (c) 奇异值σ1(k)

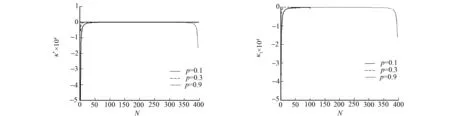
(d) κ*(k) (e) κ1(k)图3 Krawtchouk的RS系统参数计算值Fig.3 Krawtchouk′s RS system parameters calculated value

3.2Jacobsthal数列递归式稳定性分析

Jacobsthal数列的三项递归迭代公式为

图4 Jacobsthal的RS系统在Ⅱ象限跳变发散情况Fig.4 RS Jacobsthal system jumps in Ⅱ quadrant

在x=0.7，N=400的情况下，将Krawtchouk多项式整理为离散线性时变系统，其状态矩阵分解为两个旋转矩阵和一个斜变换，经SVD分解后可得

2) 对角阵S(k)的主对角线参数σ1(k)，σ2(k);

RS系统在Ⅱ象限发散，如图4所示.各个SVD分解后的数值，如图5所示.

(a) θ(k)的范围 (b) 奇异值σ1，σ2 (c) κ′(k)与κ2(k)的关系图5 Jacobsthal的RS系统参数计算值Fig.5 Jacobsthal′s RS system parameters calculated value

4 Krawtchouk多项式图像重构

结合前面的实验分析，在x=390，p=0.1，0.3，0.9的情况下，Krawtchouk多项式重构的图像，如图6所示.由图6可知：当p=0.1时，Krawtchouk多项式的递归计算误差已经增大，只能重构图像的部分；当p=0.3时，误差依旧很大，导致也只能重构部分的图像；当p=0.5时，Krawtchouk多项式递归计算的误差慢慢减小，重构的效果慢慢变好；随着阶数的增加，当p=0.9时，重构图像效果与p=0.1和p=0.3的图基本一样.

(a) p=0.1

(b) p=0.3

(c) p=0.5图6 不同p值的Krawtchouk多项式图像重构Fig.6 Image reconstruction of Krawtchouk polynomials with different p values

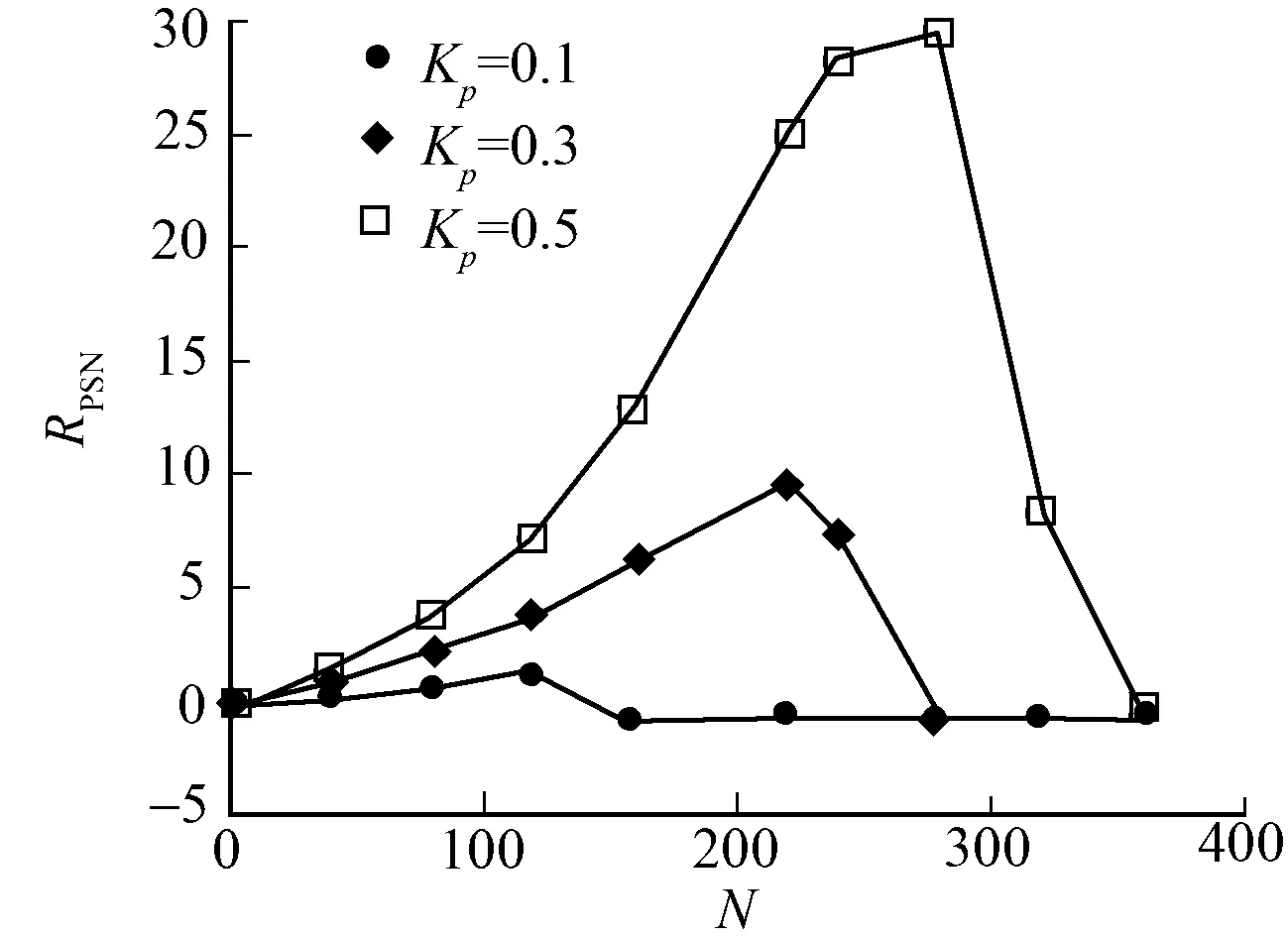
图7 Krawtchouk峰值信噪比Fig.7 Krawtchouk peak signal to noise ratio

根据图像评价标准，分别作出Krawtchouk的p值(Kp)为0.1，0.3，0.5的峰值信噪比(RPSN=10·log(2552/MSE)，MSE为均方差)，其值越高说明重构图像效果越好，如图7所示.由图7可知：Krawtchouk多项式的峰值信噪比随着阶数的增加而增加，到一定程度时，其值迅速下降.说明高阶的时候其误差是变大的导致其发散,验证了Krawtchouk正交多项式在Ⅱ,Ⅳ象限发散的情况.

5 结束语

分析和研究离散时变线性系统，将系统的状态矩阵进行奇异值分解，得到新的等效状态方程.通过分析Krawtchouk正交多项式与Jacobsthal数列递归式，计算时，通过不同的判据，说明了Krawtchouk矩阵在Ⅱ,Ⅳ象限跳变的原因，也说明了Jacobsthal数列在第Ⅱ象限发散的原因.所进行的只是初步讨论了Ⅱ,Ⅳ象限的情况，其他象限情况还有待进一步研究.

[1] 王宏伟，赵国庆.递归算法的参数设置[J].电波科学学报，2010，25(6):1187-1192,1234.

[2] 鞠宪龙.二阶对角递归神经网络的算法研究及应用[D].哈尔滨:哈尔滨工程大学，2011.

[3] 赵坚.一般二阶线性常系数齐次递归方程在数论中的应用[J].哈尔滨工业大学学报，2000，32(6):132-135.

[4] YAP P T，PARMMESRAN R，ONG S H.Image analysis by Krawtchouk moments[J].IEEE Transactions on Image Processing，2003，12(11):1367-1377.

[5] 龙爱芳，胡军浩.基于Hermite插值的高精度数值积分公式[J].华侨大学学报(自然科学版)，2013，34(3):349-352.DOI:10.11830/ISSN.1000-5013.2013.03.0349.

[6] 田萌，王文剑.基于正交多项式的核函数性质研究[J].模式识别与人工能，2014，27(5):385-393.

[7] 李炳坤.切比雪夫逼近多项式在非线性电路中的应用[J].华侨大学学报(自然科学版)，1992，13(4):558-562.DOI:10.11830/ISSN.1000-5013.1992.04.0558.

[8] 宫凤强，李夕兵.基于Legendre正交多项式逼近法的结构可靠性分析[J].工程力学，2008，25(6):225-229.

[9] MUKUNDAN R，ONG S H，LEE P A.Image analysis by tchebichef moments[J].IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society，2001，10(9):1357-1364.DOI:10.1109/83.941859.

[10] GAUTSCHI W.Computational aspects of three-term recurrence relations[J].Siam Review，1967，9(1):24-82.

[11] GAUTSCHI W.Is the recurrence relation for orthogonal polynomials always stable?[J].BIT，1993，33(2):277-284.DOI:10.1007/BF01989750.

[12] 关轶峰，李铁寿.二阶离散线性时变系统的一种稳定性判据[J].计算技术与自动化，2003，22(4):12-15.

[13] MUKUNDAN R.A comparative analysis of radial-tchebichef moments and zernike moments[C]∥Procedings of the British Machine Vision Conference.London:BMVA Press,2009:16(1-7).DOI:10.5244/C.23.16.

[14] 张海艳，高尚兵.图像分割中改进空间约束贝叶斯网络模型的应用[J].计算机应用，2017，37(3):823-826,831.DOI:10.11772/j.issn.1001-9081.2017.03.823.

(责任编辑： 陈志贤英文审校： 吴逢铁)

NumericalStabilityMethodofSecondOrderRecursiveSystemUsingSingularValueDecomposition

FU Bo， LIU Jiyuan， ZHAO Xilin， XU Guanghui, WANG Zipeng

(School of Electrical and Electronic Engineering， Hubei University of Technology， Wuhan 430068， China)

In order to solve the problem of stability of second order recursive systemsimply， the second order recursive system is transformed into second order discrete time-varying linear system and the stability of recursive system is discussed. Based on the stability analysis of second-order discrete linear time-varying systems， converting it into a reference signal (RS) system by singular value decomposition (SVD). Based on discrete orthogonal Krawtchouk polynomials and the Jacobsthal series, a new sufficient condition for discrete time-varying linear instability is proposed. The changes and new instability codes in the second and fourth quadrants are discussed and deduced. The simulation results verify the conclusion accuracy.

Krawtchouk polynomials; Jacobsthal sequences; singular value decomposition; recursive systems; linear discrete time-varying systems

10.11830/ISSN.1000-5013.201703080

TP 391

A

1000-5013(2017)06-0886-06

2017-03-30

付波(1973-)，男，教授，博士，主要从事图像处理与模式识别的研究.E-mail:fubofanxx@mail.hbut.edu.cn.

国家自然科学基金资助项目(61072130， 51309094， 61603127)； 国家教育部留学回国人员科研启动基金资助项目(20141685)； 湖北省科技厅重大科技专项项目(2013AE001)