改进的频繁和高效用项集挖掘算法

张健, 刘韶涛

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

改进的频繁和高效用项集挖掘算法

张健, 刘韶涛

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

提出一种基于局部效用质量值的上界剪枝新方法，引入伪投影技术避免真实地构造物理投影，基于二者提出改进的FHIMA-P算法.在提出的FHIMA-P算法中引入事务合并和投影事务合并技术，提出最终的FHIMA-MP算法，并在mushroom和accident数据集上进行实验.结果表明：FHIMA-P算法的运行时间相比FHIMA-ALL算法缩短，而FHIMA-MP算法则较前两者效率有非常大的提高；在不同参数下，mushroom和accident数据集中大量可合并事务(投影事务)数目也很好地证明了事务(投影事务)合并的有效性.

频繁项集； 高效用项集； 伪投影； 事务合并

关联规则最初是挖掘频繁项集[1-4]，项集的支持度大于等于最小支持度时，这个项集是频繁的.高效用项集挖掘[5-9]是频繁项集挖掘的扩展，项集的效用值大于等于最小效用值时，这个项集是高效用的.高效用项集挖掘中，每个项在事务中可以出现多次，并且可以有不同的权重，因此，高效用项集挖掘更加复杂.现有算法多将支持度和效用值单独考虑，很少将这两种衡量标准同时考虑.李慧等[10]首次将支持度和相对效用值线性加权，定义为质量值，提出挖掘数据库中高质量项集的FHIMA算法.FHIMA算法使用PrefixSpan算法[11]的思想，递归地构造前缀的投影数据库挖掘频繁和高效用项集.然而，如果是物理地复制得到投影数据库，开销很大.因此，本文引入伪投影技术进行优化,提出一种本地效用质量值上界剪枝的方法，在 FHIMA算法基础上，引入事务合并和投影事务合并技术，提出FHIMA-MP算法.

1 频繁高效用项集挖掘算法FHIMA

FHIMA算法是基于前缀投影的模式增长算法，它把支持度σ(X)和相对效用值线性加权λΦ(X)后的变量定义为质量，在给定参数下，挖掘所有高质量项集.FHIMA算法有以下3个执行步骤.1) 删去数据库中非频繁高效用项集的项(不满足最小支持度和事务效用权重估计的1-项集)，得到频繁高效用1-项集，数目为n.2) 将数据库中各条事物按≻(1-项集事务效用权重递增的顺序)排序，排序后按照≻顺序将搜索空间划分为n个具有不同前缀的投影数据库.3) 在这n个投影数据库中,递归构造子投影数据库进行挖掘，挖掘中进行算法搜索空间剪枝.

2 FHIMA算法改进

2.1局部效用剪枝和数据库伪投影

FHIMA算法的剪枝是剪掉以该节点为根的整棵子树，经过分析，在这以前如果适当减少这棵子树上的节点，得到的剪枝上界将更紧凑，结果将更高效.

在高效用项集挖掘算法中，一般第一步用事务效用权重的闭包属性[6]删去不可能从中得到高效用项集的项目.借鉴这点，提出了局部效用剪枝的概念.文中除自定义符号外，所有符号和文献[10]一致.

定义1局部效用lu(X,c)，其中，X是任意一个项集；项c∈EI(X).项集X∪c的局部效用定义为

).

性质1X是任意一个项集，对于项c∈EI(X),如果项集C是项集X通过添加EI(X)中元素后得到的项集，则有lu(X,c)≥u(C)成立.

证明 因为项集C是通过添加项集X扩展项集中元素后得到的项集，所以项集C的效用小于等于项集X的效用加上X的扩展项集中全部元素效用之和，即

X是任意一个项集，对于项c∈EI(X)，如果lu(X,c)小于最小效用值，则所有项集X的扩展项集中包含项c的都是低效用的，也就是项c这个节点可以从子树中删去.

得到基于局部效用剪枝的质量值上界计算式为

利用这个上界，从投影数据库中删去不满足条件的项目，可以进一步缩减搜索空间.

定义2以项集a为前缀的投影事务定义为α-T={i|i∈T∧i∈EI(a)}.

定义3以项集a为前缀的投影数据库定义为α-D={a-T|T∈D∧a-T≠Φ}.

在FHIMA算法中,如果物理地复制得到投影数据库，则花费在计算a-D上的时间是O(n×l)(n是投影数据库的事务数,l是事务平均长度).为了避免物理地复制，运用伪投影技术.对数据库中每一条事务添加一个偏移量指针指向它，在每条事务中查找扩展项集中第一个项相对于整条事务的偏移量，从而得到投影事务，进而得到整个数据库的伪投影.采用伪投影将a-D的算法时间复杂度降为O(n).

2.2事务合并和投影事务合并技术

事务合并是将两条或多条事务合并为一条事务，从而减少数据库规模的一种策略.

定义4称两条事务是可合并的，当且仅当它们按照规则排序后所含的项是完全相同时，而不管它们的内部效用值或支持度是否相同.

投影数据库比原来规模更小，因而,会有更多满足可合并条件的事务.

需要注意，对于投影事务合并先要得到投影数据库，得到投影数据库时项的效用值是相加，但支持数不是.应该先和它前缀项集的支持数比较，取较小的作为投影后相应项的支持数.

事务合并和投影事务合并显然会大大减少数据库的扫描次数，但关键的问题是如何高效地实现这两种合并.最直接的做法就是将所有的事务进行相互比较，看哪些是可以合并的，但这种操作算法的时间复杂度为O(n2).为了将时间复杂度降低到O(n),定义如下的偏序全排序.

定义7≻T定义在全排序≻的基础上，假设有两条事物ta={i1,i2,…,im}和tb={j1,j2,…,jk}.这个偏序全排序关系定义如下4种情况.

1) 如果这两条事物可合并，且事物编号tb大于ta，则最终偏序关系为Tb≻TTa.

2) 如果kgt;m,对任意整数x，x满足0≤xlt;m,都有im-x=jk-x，则最终偏序关系为Tb≻TTa.

3) 如果存在x是整数，x满足0≤xlt;min(m,k)，此时，对所有整数y，y满足xlt;ylt;min(m,k)且jk-x≻im-x,im-y=jk-y，则最终偏序关系为Tb≻TTa.

4) 当不满足这3种关系时，则最终偏序关系为Tb≻TTa.

按照≻T顺序排序后，可以得到性质2.根据性质2，所有可合并的事务在数据库(或投影数据库)中能通过比较相邻事务得到，这样就能在线性时间内找到它们.

性质2项集a的投影数据库a-D按T排序后，满足可相互合并的事务在排序后的投影数据库中是连续出现的.

3 实验结果与分析

3.1实验设置

为了对比算法性能，将实现FHIMA算法挖掘全部频繁高效用项集的算法命名为FHIMA-ALL，与加入伪投影和局部效用剪枝优化后的FHIMA-P算法和在FHIMA-P算法中加入事务(投影事务)合并后的FHIMA-MP算法进行对比.实验平台为Intel(R) Core(TM) i5-3470，主频 3.20 GHz,内存8 GB，Windows 7 旗舰版 64位 SP1，编程语言为Java，开发环境Eclipse 4.4.0.数据集为fimi[http:∥fimi.ua.ac.be/]网站下载的mushroom和accident数据集.和文献[6-8]中方法一样，各数据集中各项的内部效用值使用对数正态分布生成1到10之间的数，事务中各项的数量是随机生成1到10之间的数.

3.2不同参数设置的算法对比

3.2.1 支持度阈值 不同支持度下，mushroom和accident的运行时间，如图1所示.图1中：t为时间；η为最小支持度.由图1可知：支持度越小，算法挖掘的频繁和高效用项集越多，2种算法运行时间随支持度的增加开始变少,FHIMA-P算法比FHIMA-ALL算法运行时间短，FHIMA-MP算法则比前2个算法的效率更高.原因在于，首先，在数据库中，有许多满足可合并的事务，FHIMA-MP算法将它们合并成一条事务，大大压缩了事务数据库；其次，由于算法挖掘都在构造的投影数据库中进行，而投影数据库因其规模更小满足可合并要求的事务更多，所以，加入事务合并和投影事务合并技术大大提高了算法的运行效率.

(a) mushroom数据集 (b) accident数据集图1 不同支持度下mushroom和accident的运行时间Fig.1 Running time in different support on mushroom and accident dataset

(a) mushroom数据集 (b) accident数据集图2 不同支持度下mushroom和accident的事务(投影事务)合并数Fig.2 Numbers of transactions (projected transactions) that can be merged in different support on mushroom and accident dataset

不同支持度下，mushroom和accident的事务(投影事务)合并数，如图2所示.图2中：n为事务(投影事务)合并数；η为最小支持度.由图2可知：mushroom和accident数据集中，事务(投影事务)合并数随支持度的增加而减少，并且在指定支持度下，它们都存在百万级别的事务(投影事务)合并数.

3.2.2 相对效用值阈值 不同相对效用值下，mushroom和accident的运行时间，如图3所示.由图3可知:当最小相对支持度变大时，3种算法运行时间也是逐渐变少，并且3种算法效率大小关系仍和支持度从小到大变化时一致，即FHIMA-P算法比FHIMA-ALL算法运行时间更短，FHIMA-MP算法相比前两个算法运行效率有显著的提高.

不同相对效用值下，mushroom和accident的事务(投影事务)合并数，如图4所示.由图4可知：3种数据集中事务(投影事务)合并数随相对效用值的增加而减少，在最小效用值阈值下，同样存在着百万级别的事务(投影)事务合并数，这是FHIMA-MP算法比FHIMA-P算法效率更高的原因.

(a) mushroom数据集 (b) accident数据集图3 不同相对效用值下mushroom和accident的运行时间Fig.3 Running time in different relative utility on mushroom and accident dataset

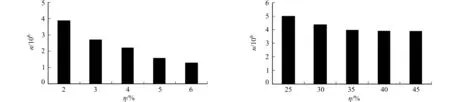
(a) mushroom数据集 (b) accident数据集图4 不同相对效用值下mushroom和accident的事务(投影事务)合并数Fig.4 Numbers of transactions (projected transactions) that can be merged in different relative utility on mushroom and accident dataset

3.2.3 加权系数阈值 加权系数λ代表相对效用值的重要程度.不同加权系数λ下,mushroom数据集上的运行时间和(投影)事务合并数，如图5所示.由图5可知：3种算法运行时间都在逐渐增加，且它们效率高低关系与支持度和相对效用的变化一致;当λ变大时，mushroom中事务(投影事务)合并数逐渐增加,当λ增加到一定程度，3种算法效率和事务(投影事务)合并数的增速都开始变缓.这是因为此时相对效用值起主导作用，再增加λ,对算法效率提升已经不明显了.

(a) 运行时间 (b) 事务(投影事务)合并数图5 不同加权系数λ下mushroom数据集上的运行时间和(投影)事务合并数Fig.5 Running time and numbers of transactions (projected transactions) that can be merged in different weighting coefficient λ on mushroom dataset

当λ=0时，FHIMA-P和FHIMA-MP算法转变为挖掘频繁项集的算法.为了比较算法在λ=0时挖掘频繁项集的效率，将FHIMA-P和FHIMA-MP算法分别与Apriori算法[1]和FpGrowth算法[2]进行比较,结果如图6,7所示.为了更直观对比效果，将对比的4个算法拆分成2幅图.

(a) FHIMA-MP和FpGrowth算法 (b) FHIMA-P和Apriori算法图6 mushroom上不同支持度下运行时间对比图Fig.6 Comparation of running time in different support on mushroom dataset

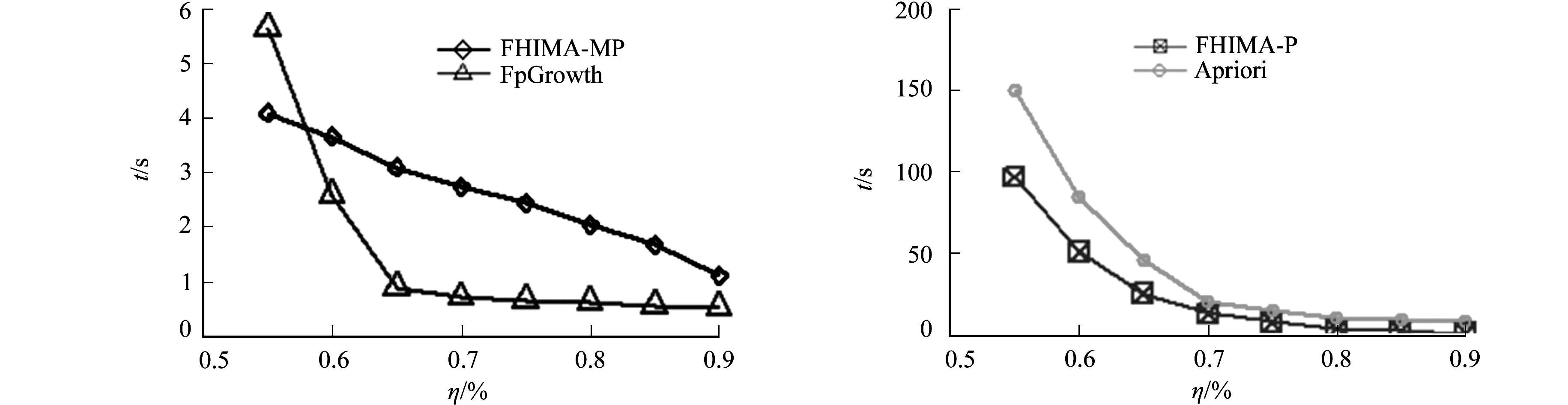
(a) FHIMA-MP和FpGrowth算法 (b) FHIMA-P和Apriori算法图7 Accident上不同支持度下运行时间对比图Fig.7 Comparation of running time in different support on accident dataset

4 结论

在FHIMA算法的基础上，引入事务伪投影和局部效用剪枝，提出改进的FHIMA-P算法.引入伪投影，避免了物理地复制构造投影数据库，另外，为了进一步减少算法搜索空间，定义了一种基于局部效用的质量值剪枝，从而提高算法效率，最终实验也证明了这种改进的有效性.最后，观察到数据库中有很多事务是可以合并的，并且由于文中算法的特点，将这种合并扩展到投影数据库中.同时，为了快速找到满足相互之间可合并条件的事务，定义了一种排序规则.实验结果证明:在FHIMA-P算法基础上,加入事务(投影事务)合并技术的FHIMA-MP算法相比于之前的FHIMA-P算法效率有非常显著地提高,另外，在加权系数为0时，FHIMA-P算法明显比Apriori算法高效，且FHIMA-P算法由于事务(投影事务)合并仍然适用效率则远高于FHIMA-P算法和Apriori算法，它的效率只比FpGrowth算法稍低，从而进一步证明了事务(投影事务)合并的高效性.

接下来，有关频繁高效用项集挖掘方法的研究，还可以从完全频繁项集、基于约束条件的频繁项集、最大频繁项集、频繁闭项集等类型着手尝试.在确定性数据中,每种类型的频繁项集都有其对应的挖掘方法，还可以将频繁高效用挖掘推广到时间序列数据、不确定数据及其他类型适合挖掘的数据上.

[1] AGRAWAL B R,SRIKANT R.Fast algorithm for mining association rules[C]∥Proc of International Conference on Very Large Data Bases.Santiago:VLDB,1994:487-499.DOI:10.1109/tencon.2003.1273266.

[2] HAN Jiawei,PEI Jian,YIN Yiwen.Mining frequent patterns without candidate generation[C]∥Proc of 2000 ACM-SIGMOD International Conference on Management of Data (SIGMOD′00).Dallas:Conference Publications,2000:1-12.DOI:10.1023/b:dami.0000005258.31418.83.

[3] DENG Zhihong,WANG Zhonghui,JIANG Jiajian.A new algorithm for fast mining frequent itemsets using N-lists[J].Sciece China Information Sciences,2012,55(9):2008-2030.DOI:10.1007/s11432-012-4638-z.

[4] DENG Zhihong,LYU Shenglong.Fast mining frequent itemsets using Nodesets[J].Expert Systems with Applications,2014,41(10):4505-4512.DOI:10.1016/j.eswa.2014.01.025.

[5] YAO Hong,HAMILTON H J,BUTZ C J.A foundational approach to mining itemset utilities from databases[C]∥Proceedings of the Fourth SIAM International Conference on Data Mining.Florida:DBLP,2004:482-486.

[6] LIU Ying,LIAO Weikeng,CHOUDHARY A.A two-phase algorithm for fast discovery of high utility itemsets[C]∥PAKDD′05 Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining.Hanoi:Springer Berlin Heidelberg,2005:689-695.DOI:10.1007/11430919_79.

[7] TSENG V S,WU C W,SHIE B E,etal.UP-Growth: An efficient algorithm for high utility itemset mining[C]∥Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Washington D C:ACM Press,2010:253-262.DOI:10.1145/1835804.1835839.

[8] LIU Mengchi,QU Junfeng.Mining high utility itemsets without candidate generation[C]∥ACM International Conference on Information and Knowledge Management.New York:ACM Press,2012:55-64.

[9] KRISHNAMOORTHY S.Pruning strategies for mining high utility itemsets[J].Expert Systems with Applications,2015,42(5):2371-2381.DOI:10.1016/j.eswa.2014.11.001.

[10] 李慧,刘贵全,瞿春燕.频繁和高效用项集挖掘[J].计算机科学,2015,42(5):82-87.DOI:10.11896/j.issn.1002-137X.2015.05.017.

[11] PEI Jian,HAN Jiawei,MORTAZAVI-ASL B,etal.PrefixSpan: Mining sequential patterns efficiently by prefix-projected pattern growth[C]∥Proceedings of the 17th International Conference on Data Engineering.Washington D C:IEEE Press,2001:215-224.DOI:10.1109/icde.2001.914830.

(责任编辑： 黄晓楠英文审校： 吴逢铁)

ImprovedMiningAlgorithmforFrequentandHighUtilityItemsets

ZHANG Jian， LIU Shaotao

(College of Computer Science and Technology, Huaqiao University, Xiamen 361021, China)

A new method that uses the upper bound of quality to prune the search space based on local utility quality is proposed, meanwhile, pseudo projection technique is introduced to avoid actually construct the physical projection, then based on these two points, an improved FHIMA-P algorithm is proposed. By adding the transaction merging and projected transaction merging technique in FHIMA-P algorithm, the final FHIMA-MP algorithm is proposed. An experiment is conducted on mushroom and accident dataset, the result shows that the running time of FHIMA-P algorithm is shorter than that of FHIMA-ALL algorithm, while the FHIMA-MP algorithm improves significantly compared with the previous two algorithms′ efficiency. Moreover, the huge number of transactions (projected transaction) that can be merged on mushroom and accident dataset in different papameters also prove the effectiveness of transaction (projected transaction) merging technique.

frequent itemsets； high utility itemsets； pseudo projection； transaction merging

10.11830/ISSN.1000-5013.201603067

TP 311

A

1000-5013(2017)06-0880-06

2016-03-24

刘韶涛(1969-)，男，副教授，主要从事软件体系结构与软件复用的研究.E-mail:shaotaol@hqu.edu.cn.

福建省科技计划重大项目(2011H6016)