Kaplansky计数命题的拓广及应用

唐善刚

(西华师范大学 数学与信息学院, 四川 南充 637009)

Kaplansky计数命题的拓广及应用

唐善刚

(西华师范大学 数学与信息学院, 四川 南充 637009)

应用组合分析技巧,给出基于线排列与环形排列情形下的经典的Kaplansky计数命题的拓广情形，得到了两个推广后的新的Kaplansky计数命题.通过推广Ménage计数问题以及组合恒等式的证明，所得结果拓展了已有文献的研究结果.

Kaplansky计数命题； Ménage计数问题； 线排列； 环形排列； 组合恒等式； 容斥原理

Kaplansky计数命题在Ménage计数问题[1-5]、二重乱序的计数公式[6]、限位排列[7-13]，以及第一、二类可重环形排列[7-13]中有着广泛的应用，其基本形式可表述为基于线排列与环形排列情形下的组合计数命题.

文献[6]将定理1，2推广为定理3，4.

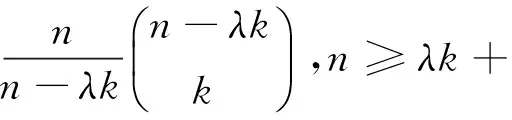
1 Kaplansky计数命题的再拓广

进一步将定理3,4拓广为基于如下的线排列与环形排列情形下的组合计数命题.

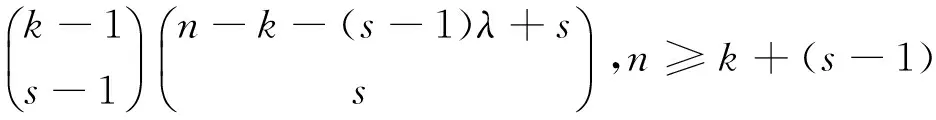
证明 先假定1lt;klt;n,设{ai,1,ai,2,…,ai,yi|1≤i≤s}是从全排列a1a2…an中选出的符合题意的k元组合，设段ai,1,ai,2,…,ai,yi与段a(i+1),1,a(i+1),2,…,a(i+1),yi+1之间在全排列a1a2…an中间隔的元素个数为xi+1(1≤i≤s-1)；段a1,1,a1,2,…,a1,y1在全排列a1a2…an之前的元素个数为x1；段as,1,as,2,…,as,ys在全排列a1a2…an之后的元素个数为xs+1.据此，可得如下的不定方程组,即

式(1)中:x1,xs+1≥0；xi≥λ(i=2,3,…,s)；yjgt;0(j=1,2,…,s).

据此，得到从全排列a1a2…an中选取符合题意的k个元素的组合的个数为

n.

1) 若k=1，必有s=1.显然，此时符合题意的k个元素的组合的个数为n，且

n.

2) 若k=n时，必有s=1.显然，此时符合题意的k个元素的组合的个数为1，且

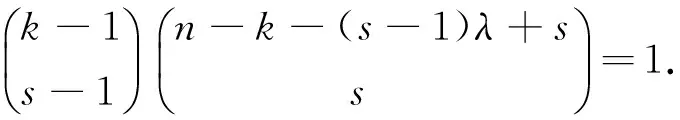
3) 若s=1.显然，此时符合题意的k个元素的组合的个数为n-k+1，且

综上所述，从全排列a1a2…an中选取符合题意的k个元素的组合的个数为

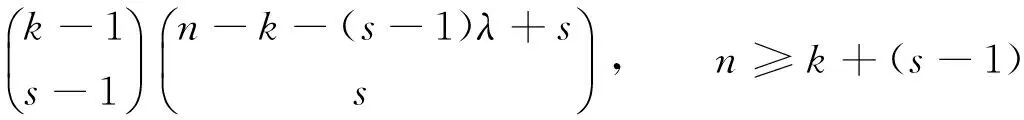
λ.

证明 先假定1lt;klt;n.设{ai,1,ai,2,…,ai,yi|1≤i≤s}是从⊙a1a2…an中选出的符合题意的k元组合，于是⊙a1a2…an中不属于{ai,1,ai,2,…,ai,yi|1≤i≤s}的元素可能为aj+1,aj+2,…,aj+λ(1≤j≤n).

⊙a1a2…an中不属于{ai,1,ai,2,…,ai,yi|1≤i≤s}的元素aj+1,aj+2,…,aj+λ(1≤j≤n)，其下标j+1,j+2,…,j+λ约定为j+1,j+2,…,j+λ分别除以n所得到的最小正剩余数，例如，当j=n-1时，元素an,an+1,an+2,…,an+λ-1即为an,a1,a2,…,aλ-1.

据此，按照如下4个步骤求解.

步骤1设从环形排列⊙a1a2…an中选取符合题意的k元组合为{ai,1,ai,2,…,ai,yi|1≤i≤s}，且使得aj+1,aj+2,…,aj+λ不属于{ai,1,ai,2,…,ai,yi|1≤i≤s}的组合的个数为dj,1≤j≤n.

根据定理5，求dj等价于求如下不定方程组的整数解(x1,y1,x2,y2,…,xs,ys,xs+1)的个数，即

式(2)中：x1,xs+1≥0；xi≥λ(i=2,3,…,s)；yjgt;0(j=1,2,…,s).

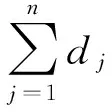
步骤4根据步骤3的结果，从环形排列⊙a1a2…an中选取k个元素，并使得这k个元素被环形排列⊙a1a2…an中其余元素分隔成s段，且任何两段之间在环形排列⊙a1a2…an中至少还间隔有λ个元素的组合的个数为

n.

1) 若k=1时，必有s=1.显然，此时符合题意的k个元素的组合的个数为n，且

n.

2) 若s=1时，显然，符合题意的k个元素的组合的个数为n，且

n.

综上所述，从环形排列⊙a1a2…an中选取符合题意的k个元素的组合的个数为

k.

2 Kaplansky计数命题的应用

Ménage计数问题是一个著名的组合学问题，由法国数学家Lucus提出，即求n对夫妻围圆桌而坐，且男女相间夫妻不相邻的坐法数.1986年，Bogart等[1]又提出了所谓的不要求男女相间的“放松的夫妻对围坐计数问题”.文献[2-3]利用容斥原理将Ménage计数问题推广为多维情形下的计数问题加以研究.文中将经典的Ménage计数问题推广为如下情形.

Ménage计数问题的拓广如下：有n组学生，且每组学生中男、女生人数均为λ人,n组学生围圆桌而坐.设α与β是n组学生围圆桌而坐的两种坐法方式,α=β当且仅当每个学生在α及β中与之相邻的人组成的集合是相等的.

1) 求满足上述约定下的n组学生男女相间围圆桌而坐，且恰好有r组学生中的每组学生是坐在一起的坐法方式数f1(n,λ).

2) 求满足上述约定下的n组学生男女相间围圆桌而坐，且恰好使得其中指定的r组学生中的每组学生是坐在一起的坐法方式数f2(n,λ).

3) 求满足上述约定下的n组学生男女相间围圆桌而坐，且至多有r组学生中的每组学生是坐在一起的坐法方式数f3(n,λ).

4) 求满足上述约定下的n组学生男女相间围圆桌而坐，且至少有r组学生中的每组学生是坐在一起的坐法方式数f4(n,λ).

为行文方便起见，对围圆桌的2λn个座位按照逆时针方向以自然顺序编号，其座位号分别标记为1,2,3,…,2λn.

2) 不妨设满足情形1)下的k个座位的组合为{i1,i2,…,ik}，且组合{i1,i2,…,ik}必然与含有2λk个座位的组合{is,is+1,is+2,…,is+2λ-1|1≤s≤k}之间存在一一对应的关系.将指定的某组学生男女相间安排在座位i1,i1+1,i1+2,…,i1+2λ-1上入坐的坐法方式数为2(λ!)2；而将指定的另外某组学生男女相间安排在座位is,is+1,is+2,…,is+2λ-1上入坐的坐法方式数为(λ!)2，2≤s≤k；最后，剩余的n-k组学生男女相间入坐在剩余的2λn-2λk个座位上的坐法方式数为((λn-λk)!)2.

由于围圆桌而放置的座位是带有标号的，故组合{is,is+1,is+2,…,is+2λ-1|1≤s≤k}中代表座位编号的具体数字都约定为它们除以2λn后所得的最小正剩余数.

显然n组学生男女相间围着带有标号的2λn个座位的圆桌而坐的坐法方式数为2((λn)!)2，即

当k=0时,上式仍然成立.

4)fi(n,λ)即为二面体群D2λn作用于由2λn个学生男女相间围着带有标号的2λn个座位的圆桌而坐的所有坐法方式构成的集合的轨道数(1≤i≤4).运用Burnside引理[8-13]及容斥原理[2-3,14-16]，即得定理7.

定理7推广的Ménage计数问题的结果为

定理8证明下列组合恒等式

2) 求由数字1,2,…,n组成的不含数对(i,i+1)(i=1,2,…,n-1)的全排列的个数.令A表示由数字1,2,…,n组成的所有全排列的集合，对于π∈A，数对(i,i+1)界定命题Pi(π)为Pi∶π中含有数对(i,i+1)，其中，i=1,2,…,n-1.

据此有

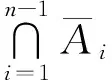
从而有

3 结束语

将文献[6]的Kaplansky计数命题推广至更具一般化情形下的基于线排列与环形排列下的新的组合计数命题，从理论上拓宽了经典的Kaplansky计数命题的适用范围；给出了从理论上推广后的新的Kaplansky计数命题在具体组合问题中的应用，拓展了相关文献的结果.

[1] 林翠琴.组合学与图论[M].北京:清华大学出版社,2009.

[2] 唐善刚.关于“容斥原理的拓广及其应用”的注记[J].山东大学学报(理学版),2012,47(10):64-69. DOI:10.6040 /j.issn． 1671-9352.2012.10.014.

[3] 唐善刚.赋权有限集上的容斥原理及应用[J].浙江大学学报(理学版),2014,41(2):123-126.DOI:10.3785/j.issn.1008-9497.2014.02.001.

[4] 曹汝成.广义容斥原理及其应用[J].数学研究与评论,1988,8(4):526-530.

[5] 魏万迪.广容斥原理及其应用[J].科学通报,1980,25(7):296-299.

[6] 李磊.关于几个组合计数公式的推广[J].工程数学学报,1996,13(4):95-98.

[7] 李乔.组合数学基础[M].北京:高等教育出版社,1993.

[8] 卢开澄,卢华明.组合数学[M].4版.北京:清华大学出版社,2006.

[9] 许胤龙,孙淑玲.组合数学引论[M].2版.合肥:中国科学技术大学出版社,2010.

[10] 柯召,魏万迪.组合论[M].北京:科学出版社,1981.

[11] 屠规彰.组合计数方法及其应用[M].北京:科学出版社,1981.

[12] 姜建国,岳建国.组合数学[M].西安:西安电子科技大学出版社,2003.

[13] 曹汝成.组合数学[M].广州:华南理工大学出版社,2000.

[14] 唐善刚.容斥原理的拓展及其应用[J].山东大学学报(理学版),2010,45(12):12-15.

[15] 唐善刚.容斥原理的拓展及其应用(Ⅱ)[J].山东大学学报(理学版),2011,46(12):70-75.

[16] BENDER E A,GOLDMAN J R.Mobius inversion in combinatorial analysis[J].Amer Math Monthly,1975(82):789-802.DOI:10.3785/j.issn.1008-9497.2014.02.001.

(责任编辑： 陈志贤英文审校： 黄心中)

GeneralizationsofKaplanskyEnumeratingTheoremsandItsApplications

TANG Shangang

(College of Mathematics and Information, China West Normal University, Nanchong 637009, China)

By using combinatorial analysis we extend Kaplansky enumerating theorems are to the general conditions under a linear permutation and a circular permutation. Two generalized theorems for the Kaplansky enumerating theorems are obtained. One class of Ménage enumerating problem is extended and some combinatorial identities are proved with the generalized Kaplansky enumerating theorems. Our results generalize those of the previous studies.

Kaplansky enumerating theorem; Ménage enumeratiing problem; linear permutation; circular permutation; combinatorial identity; principle of inclusion-exclusion

10.11830/ISSN.1000-5013.201607009

O 157.1

A

1000-5013(2017)06-0892-06

2016-07-05

唐善刚(1978-)，男，副教授，主要从事组合计数方法理论及应用的研究.E-mail:tangshangang2001@163.com.

国家自然科学基金资助项目(11401480)； 四川省教育厅自然科学基金重点项目(16ZA0173, 17ZA0383)