超声滚压加工再生型颤振系统的稳定性分析
张 明,姚 静,刘让雷
(青岛科技大学机电工程学院,山东青岛266061)
超声滚压加工再生型颤振系统的稳定性分析
张 明,姚 静,刘让雷
(青岛科技大学机电工程学院,山东青岛266061)
基于超声波滚压加工,探讨了加工过程中颤振的产生机理及控制途径。首先,将工件简化为转子模型、将滚压装置简化为单自由度的振动系统,建立了再生型滚压加工的颤振模型,并进行了特性分析。基于Matlab/Simulink仿真功能,绘制出不同滚压宽度值时的时域图,得到振动系统发生颤振的临界极限状态。仿真结果与理论分析计算的极限滚压宽度相符,对实际加工中抑制颤振现象具有积极的指导作用。
超声波滚压加工;再生型颤振;极限滚压宽度;仿真
随着超声加工技术的应用越来越广泛,其在很多领域内发挥了突出的作用,工艺效果十分显著[1]。超声滚压对改变零件表面质量的耐磨性、抗疲劳性、抗蚀性有很好的提高作用[2]。超声加工中的颤振会影响机床的性能,降低工件的表面质量及加工精度,因此,对颤振的预测和控制非常重要[3]。
在滚压过程中,时常出现后一次进给与前一次进给的加工区域发生部分重叠的情况。如果加工过程中受到一个偶然的瞬时扰动,刀具与工件之间便会发生相对振动,其振幅会因阻尼作用而逐渐衰减,但这种振动会在工件表面留下一段振纹[4]。当工件转过一圈后,工具头将在留有振纹的工件表面重复滚压,导致滚压厚度发生波动,进而产生动态交变力,这种振动会进入一种持续自激振动的状态[5],从而形成由振纹和动态切削力相互影响的再生型颤振。颤振会造成工件表面精度降低、工具头破损及产生噪声,因此极大降低了加工生产率和加工质量[6-7]。
1 再生型颤振的动力学建模及稳定性分析
1.1 超声滚压加工的工作原理
超声滚压加工是利用超声波冲击能量和静载滚压相结合的工作方式,对工件表面进行滚压处理。超声波滚压装置见图1,通过滚压工具头沿工件表面法线方向施加一定幅度的超声频机械振动,在一定的进给条件下,超声波滚压工具头会将静压力和超声波冲击振动传递到旋转的机械零部件表面,产生的冲击作用使工件材料发生弹塑性变形[8]。加工后,工件表面产生一定的弹性恢复,所产生的塑性流动将工件表面的“谷”被“峰”填满或部分填满,从而大大降低表面粗糙度值,并提高表面综合性能指标。

图1 超声波辅助滚压加工装置简图
1.2 再生型颤振的动力学建模
本文主要研究单自由度滚压颤振模型,故将模型转化为“弹簧-阻尼”单自由度系统(图2)。

图2 超声滚压的动力学模型
传统颤振研究认为,机床结构刚度是线性的。在滚压加工过程中,滚压力是一个周期函数,假设动态滚压力与滚压宽度的变化量成正比,则系统的运动方程可表示为:
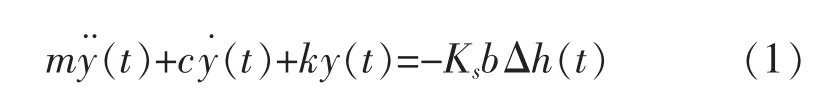
式中:m为滚压颤振系统的质量,kg;c为颤振系统的等效阻尼,(N·s)/mm;k为颤振系统的等效刚度,N/mm;b 为滚压宽度,mm;Δh(t)为滚压深度的瞬态变化量;Ks为颤振系统中的动态滚压力系数。
瞬时滚压深度为:

式中:μ 为重叠系数,μ=(b-f)/b,0<μ<1;y(t)为本次滚压的振纹;y(t-T)为上次滚压的振纹;h0为理论滚压厚度;h(t)为实际滚压厚度。
设 y(t)=acos(ωt),则:

式中:a为等幅谐波的幅值。
将式(3)代入式(2)得到:

设 A=1-μcos(ωT),B=μsin(ωT),则:
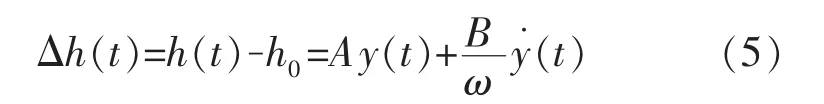
将式(5)代入式(1)得到:

式中:c=2ζmωn,ζ为滚压振动系统的等效阻尼比;wn为滚压振动系统的固有角频率,rad/s,且ωn2=k/m。
将式(6)进行拉普拉氏变换,则:
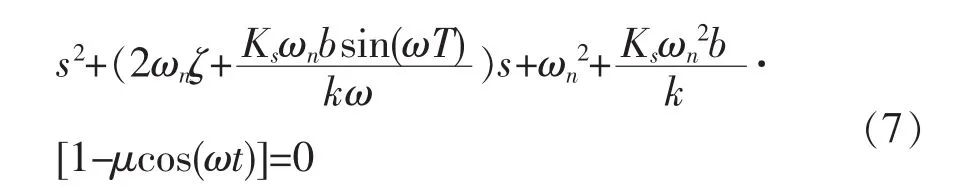
滚压振动系统的稳定性取决于其特征方程根s,设 s=α+iω,当 α>0 时,系统不稳定;当 α<0 时,系统稳定;当α=0时,系统在稳定和不稳定的临界处。
让 α=0,此时 s=iw,则:

等式两边实部与虚部分别相等,则:

将式(9)中的两式相除,且令 λ=ω/ωn,整理得:

由式(10)解得:

由于正弦函数是周期为2π的周期函数,对式(11)求解得:

式中:j=1,2,3,4,…,J。
将T=60/n代入式(12)得到转速n为:

取j=0,代入式(9)得到的临界滚压宽度b为:

2 极限滚压宽度下的Simulink仿真
采用Matlab软件的Simulink工具箱对超声滚压加工进行时域仿真,获取滚压过程在稳定、颤振状态时的振动时域信号特征,这对颤振的监测及抑制有很大的参考作用。再生型系统颤振的方程为:

对式(15)采用积分方式建立仿真模型结构(图3),并按表1所示的数据设定参数值。

表1 仿真参数

图3 滚压再生颤振仿真框图
当系统发生颤振时,系统振动频率等于系统固有频率,令ω=ωn,振动系统的固有频率ωn为:
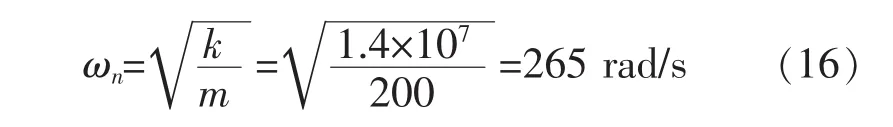
阻尼比ζ为:
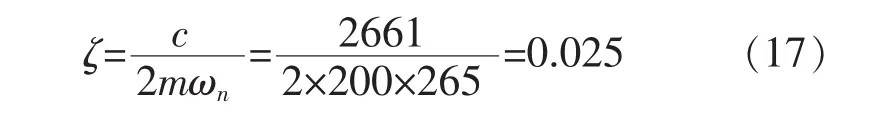
由式(15)可求出系统临界滚压宽度最小值为:

通过主轴转速计算出前、后两次的时间差:T=60/n=60/688=0.087 s。当滚压宽度b取不同值时,观测到的仿真时域图见图4。可看出,振动系统存在发生颤振的临界状态。当b=4.6 mm时,振动波形逐渐减小到平稳振动状态,即当振动系统受到外界因素干扰时,能很快地将这些因素消除掉,系统处于稳定滚压状态。当b=5.81 mm时,系统的振动近似为等幅振动,即当振动系统受到外界因素干扰时,几乎不能将这些因素消除掉,系统处于稳定与颤振的临界状态。当b=6.5 mm时,振动波形突然增大,即当振动系统受到外界因素干扰时,系统幅值比稳定状态时明显扩大,且将趋于无穷大,此时系统出现很大的稳态误差,系统处于颤振状态。
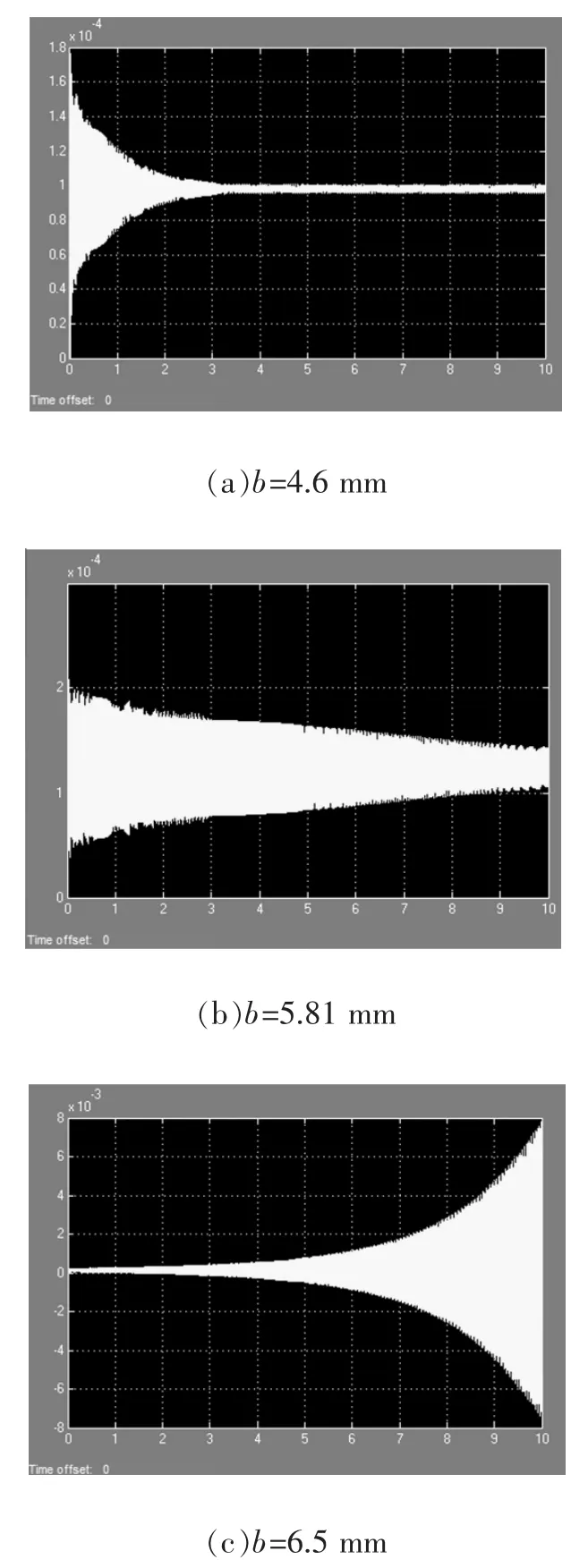
图4 不同滚压宽度下的仿真时域图
将式(18)求得的系统临界滚压宽度最小值与仿真时域图进行比较,证明计算结果与仿真结果相吻合。
3 结束语
通过对再生型颤振进行建模和特性分析,推算出振动系统的极限滚压宽度计算公式。当滚压宽度小于极限滚压宽度时不会发生颤振现象,系统处于稳定滚压状态;当滚压宽度大于临界极限宽度时,系统处于颤振状态。通过Matlab软件的Simulink工具箱对振动系统进行仿真,从仿真时域图得到振动系统发生颤振时的极限滚压宽度。当滚压宽度小于极限滚压宽度时不会发生颤振现象,且仿真结果与理论计算的临界极限滚压宽度最小值一致,从而验证了理论分析的正确性。
[1]曹凤国.超声加工技术 [M].北京:化学工业出版社,2005.
[2]张旭.超声滚压装置设计与工艺研究[D].长沙:中南大学,2014.
[3]赵铁民,牛兴华,王添丁,等.基于机床稳定性的铣削力系数的研究[J].天津理工大学学报,2016,32(1):40-43.[4]唐红霞.超声波辅助滚压加工技术机理及应用研究[D].青岛:青岛科技大学,2014.
[5]刘习军,陈予恕.机床速度型切削颤振的非线性研究[J].振动与冲击,1999,18(2):5-9.
[6]李金华,谢华龙,盛忠起,等.数控车削过程再生型颤振稳定性建模与仿真 [J].东北大学学报 (自然科学版),2013,34(1):118-122.
[7]郭瑞琴,武帅,李中.外圆车削加工过程中再生型颤振的建模与分析 [J].中国工程机械学报,2015,13(3):252-257.
[8]任学冲,陈利钦,刘鑫贵,等.表面超声滚压处理对高速列车车轴钢疲劳性能的影响 [J].材料工程,2015(12):1-5.
Stability Analysis of Ultrasonic Rolling Process Regenerative Chatter System
ZHANG Ming,YAO Jing,LIU Ranglei
(College of Electromechanical Engineering,Qingdao University of Science and Technology,Qingdao 266061,China )
Based on the ultrasonic rolling process,discusses the generation mechanism of chatter and the control approach in the process of machining.Firstly,the machined workpiece is simplified as rotor model and the rolling device is simplified as single freedom of vibration system,the flutter model of regenerative rolling process is established,and the characteristic analysis is carried out.Based on the Matlab/Simulink simulation function,the critical limit state of flutter in a vibration system is obtained by plotted the time domain chart of rolling width of different values.The simulation results accord with the limit rolling width calculated by theoretical analysis,it has positive guiding role for the chatter suppression in actual processing.
ultrasonic rolling process;regenerative chatter system;limit rolling width;simulation
TG663
A
1009-279X(2017)05-0046-03
2017-08-01
张明,男,1960年生,教授。

