低轨卫星精密定轨的轨道精度评估方法研究

袁俊军,孟瑞祖

(山东科技大学 测绘科学与工程学院,山东 青岛 266590)

低轨卫星精密定轨的轨道精度评估方法研究

袁俊军,孟瑞祖

(山东科技大学 测绘科学与工程学院,山东 青岛 266590)

厘米级精密卫星轨道是完成低轨卫星承担的科研、商业等任务的必须前提,其中事后轨道精度评定是低轨卫星精密定轨任务中重要一环。依据观测条件和卫星搭载设备等情况,选择合适的精度评定方法有利于客观准确的评估定轨结果。本文以GRACE卫星为例,讨论了内外精度评估方法,得到有益结论,为我国开展后续国产卫星精密定轨任务具有借鉴意义。

低轨卫星;精密定轨;精度评估;内外符合精度

0 引 言

目前我国众多低轨(LEO)卫星, 如资源三号,海洋二号,风云系列卫星等,发射升空,实现厘米级高精度精密定轨成为保障完成LEO卫星承担的科研任务的重要前提和研究热点[1-2]。LEO卫星精密定轨任务中,事后轨道精度评估是重要一环,综合多种方法进行轨道评估能够确保轨道精度评价的可靠性和精确性,尤其是不同观测条件下,需要选择合适的评估方法。本文以GRACE卫星为例,讨论了常用的内、外符合精度评估方法,并分析了相应方法的适用性,对我国国产低轨卫星轨道精度评估具有借鉴意义。

1 简化动力学定轨原理

低轨卫星位于地球外200～2000 km范围内绕地球运动,处于大气层中间,受到包括地球引力、日月引力、地球非球形摄动力、潮汐摄动、大气阻力、太阳辐射压、地球辐射压以及相对论效应影响等多种力的作用,结合牛顿定律,低轨卫星运动微分方程可表示为

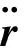
(1)

假设先验轨道r0(t)为已知,动力法定轨可视为是一个改善轨道的过程。对r(t)进行泰勒级数展开,并消去未知扰动力参数部分,则真实轨道r(t)可由参数pi的先验值pi0表示:

(2)

式中,pi为轨道参数;n=6+d表示未知参数的个数,6个初始轨道元素与d个动力参数。

简化动力学方法在采用力学模型和数值积分求解轨道时引入伪随机脉冲参数来平衡观测数据和力学摄动对定轨结果的影响,即每隔一段时间在卫星径向、切向和法向上附加伪随机脉冲参数,如大气阻力摄动、相对论摄动、以及地球红外辐射和地球反射压摄动等[3-5]。

2 精度评估方法

2.1内符合精度评估

内符合精度评估是指仅利用了定轨过程中相关数据进行分析评定定轨精度。其中,观测值残差统计,外部轨道比较,重叠弧段对比,衔接点对比等是常用的方法[6]。

2.1.1 观测值残差统计

GPS观测值残差不能完全反应轨道精度,但是残差RMS值在一定程度体现了选用力学模型以及数据预处理情况,因此,在观测值充足下,可以选用该方法评定定轨内符合精度[7]。观测值残差可以通过定轨后的观测值-计算值(O-C)获取。

2.1.2 外部轨道对比

外部轨道对比是较为常用且可靠的精度评估手段,选用不同定轨机构或者定轨软件得到的轨道,尤其是著名解算机构发布的精密轨道,作为参考轨道,可以反映定轨精度。其计算公式为

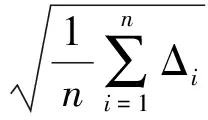
(3)

式中：n为历元数； Δi为第i个历元简化动力学轨道与参考轨道在径向、切向、法向或位置方向上的残差。

2.1.3 重叠弧段对比

重叠弧段对比是指选取30 h(或者其他定轨弧长)观测时段,前后有6 h重复计算轨道,示意图如图1所示。尽管这6 h的观测数据相同,但这两段轨道是通过两次独立解算得到,可认为这两段6 h重叠轨道不相关,因此,轨道重叠部分的符合程度反映了轨道精度。为减小边界效应的影响,在评估重叠轨道的精度时可取中间3～4 h的数据作为评估轨道精度的有效数据。计算公式与独立轨道对比方法相同[2,6,8]。

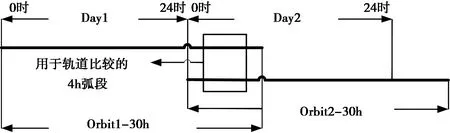
图1 轨道重叠示意图

2.2外符合精度评估

外符合精度评估是指利用独立于定轨系统的数据或方法,对定轨结果进行评估,其中,SLR检核站星距是公认的高精度外符合检验方法。若低轨卫星搭载其他检验设备,如DORIS系统,K波段测距仪,加速度计等,也可以作为独立的外符合精度评估手段。本文仅介绍SLR检核评估和K波段测距两种评估手段。

2.2.1SLR检核评估

利用SLR数据检核定轨结果,实际就是比较SLR直接测得的站星距离和星载GPS定轨结果反算的站星距,SLR残差即为两者站星距之差,为保证SLR检核可靠性,必须考虑SLR质心改正等各项改正[9-10]。

2.2.2 K波段测距

K波段测距仪是一种高精度距离测量系统,尽管它只能测量两颗卫星的相对基线距离,但是精度可达到10-6量级,因此,如果低轨卫星搭载此系统,可作为重要的外符合精度评估手段[11-12]。其基本原理就是利用两颗卫星定轨后反算出的卫星间基线距离与K波段测距仪直接测得距离进行比较。

3 GRACE卫星定轨精度分析

本文选取GRACE卫星为研究对象,采用2016年1月1日至10日GFZ发布的GPS观测数据(GPS1B),星载姿态数据(SCA1B),K波段数据(KBR1B),事后精密轨道(GNV1B),以及CODE发布的GPS精密星历和30 s采样钟差。定轨软件平台采用BERNESE5.2精密定轨软件,选用非差简化动力学方法,基于统计定轨原理和最小二乘批处理算法确定低轨卫星精密轨道[13]。选取的力学模型与参数设置如表1所示。

表1 力学模型与参数设置

3.1内符合精度

3.1.1 观测值残差统计

图2 非差载波和伪距无电离层组合观测值残差的均方差

如图2所示,LC观测值的残差的RMS平均为5.23 mm,与GRACE卫星标称的接收机噪声[14]5 mm基本相符,说明该卫星载波观测值精度较高,相位预处理(周跳探测等)较为完善。PC观测值的残差的RMS平均为0.83 m,相对于载波精度稍低,但对于PC观测值的权重较低,对定轨结果影响不明显。图3和图4示出了具体的随高度角变化的残差序列,可知低高度角观测值残差较大。这主要是由于高度角过低,LEO卫星接收机的信号捕捉能力较差,造成观测数据质量较差。因此,在定轨过程中,可设置截止高度角,预先删除观测质量较差的低高度角数据。本文在后续定轨中设置截止高度角为3°.

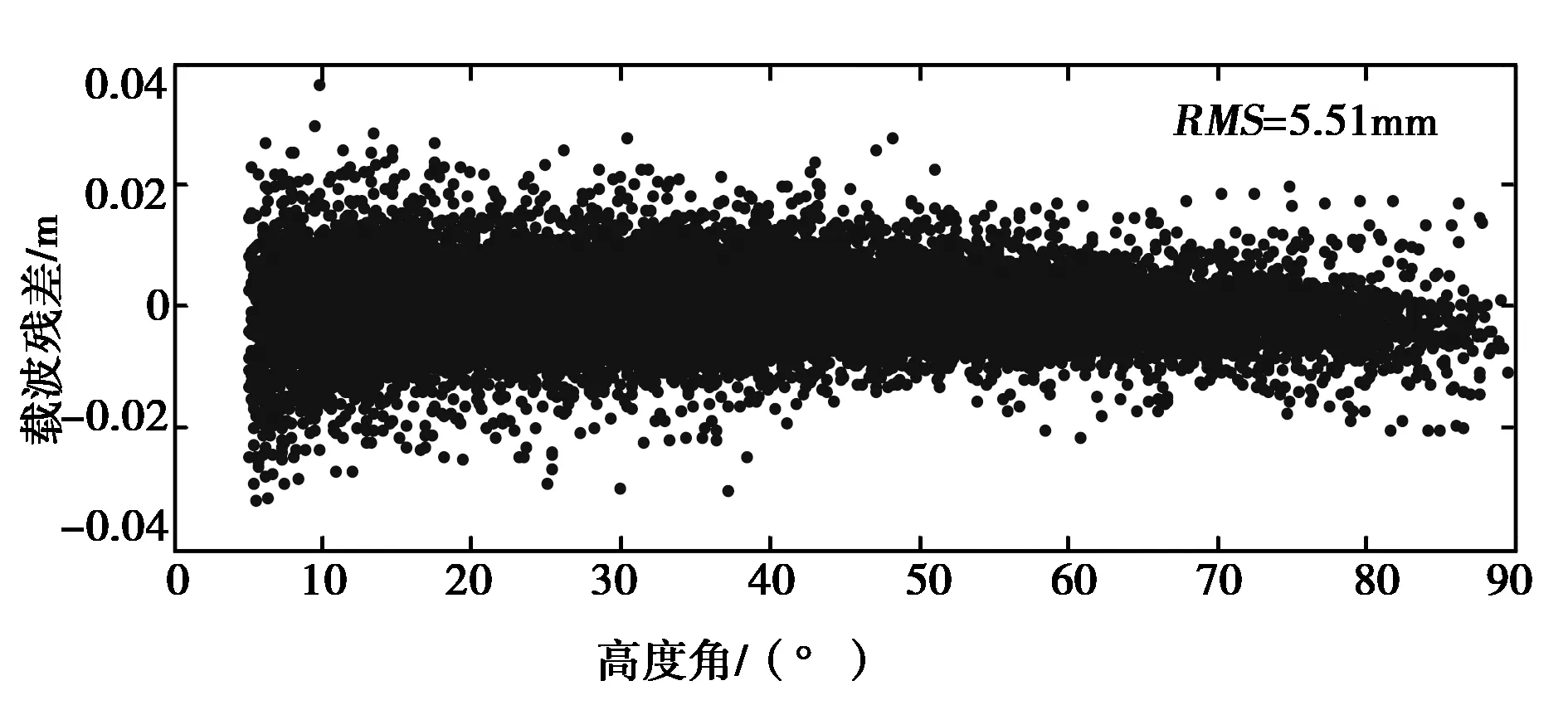
图3 年积日001d至010d的载波平均观测值残差序列图

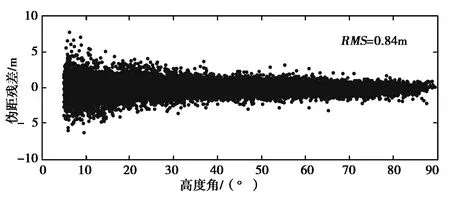
图4 年积日001d至010d的伪距平均观测值残差序列图

3.1.2 重叠弧段检核

在缺少外部精密轨道检核时,重叠弧段是重要的内符合精度评定手段。由图5,表2可以看出,重叠弧段坐标分量的精度均优于1.5 cm,径向RMS平均为0.31 cm,位置精度平均为0.91 cm,GRACE-A卫星精密轨道拟合效果较好。

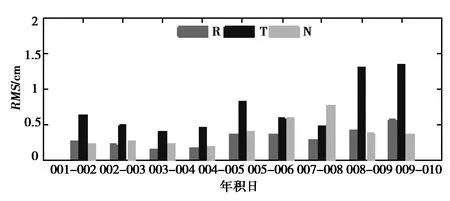
图5 GRACE-A卫星重叠弧段精度统计

表2 GRACE-A卫星重叠弧段平均精度统计/cm

3.1.3 外部轨道对比

该评估方法采用的参考轨道为JPL事后精密轨道,其定轨精度得到广泛验证,定轨精度在2～3 cm[15],采样间隔为1 min.GRACE-A精密轨道为星载GPS数据精密定轨结果,弧长为30 h.GRACE-A卫星简化动力学轨道与JPL精密轨道对比残差与精度统计如图6及表3所示。在RTN坐标系下,R方向精度较高,RMS优于2 cm;T方向略差一些,RMS在2 cm左右;N方向残差较大,RMS均值为4.23 cm;位置精度基本优于5 cm,证明了本次定轨结果的可靠性和准确性。

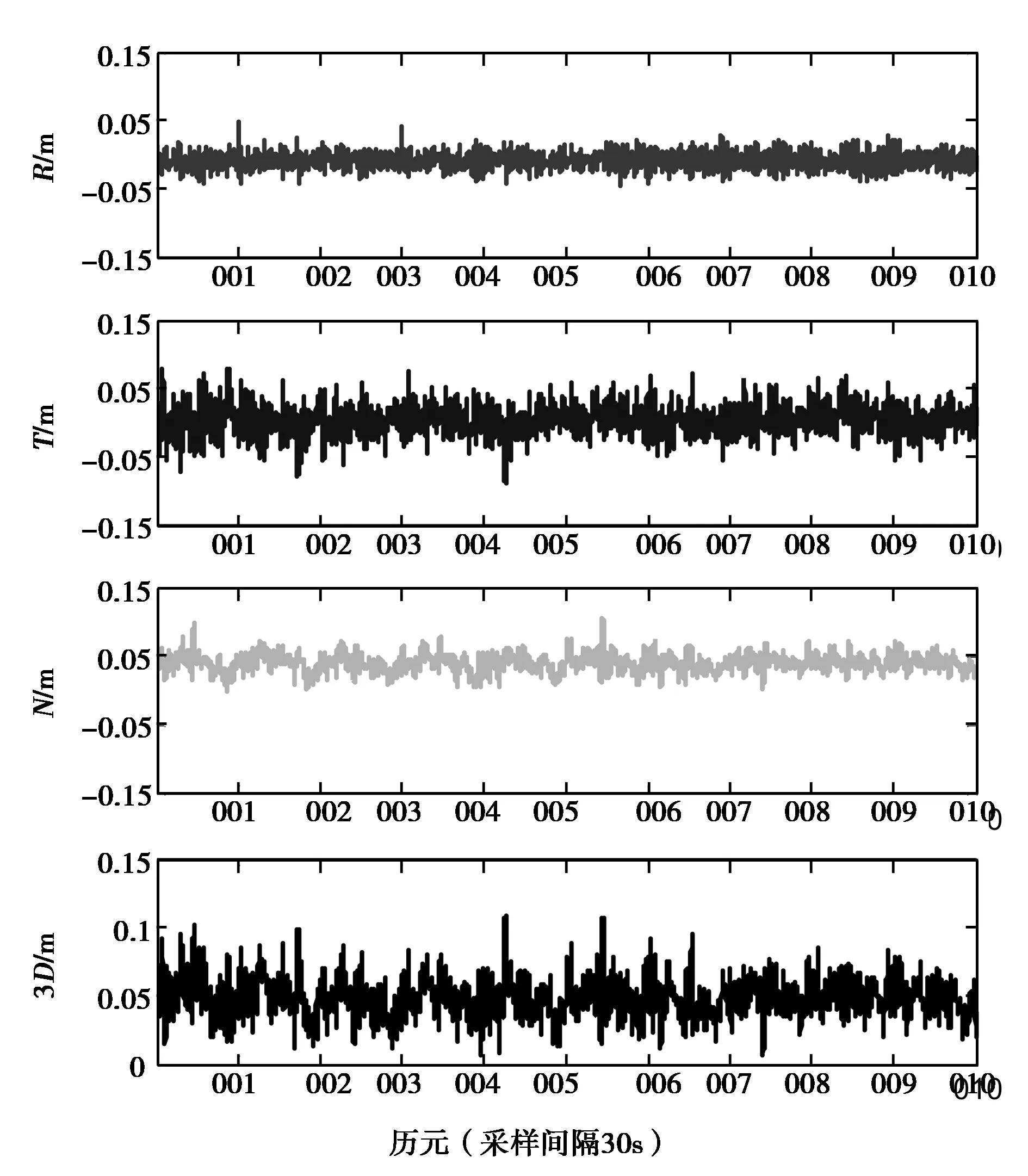
图6 GPS定轨结果与JPL精密轨道对比残差时间序列

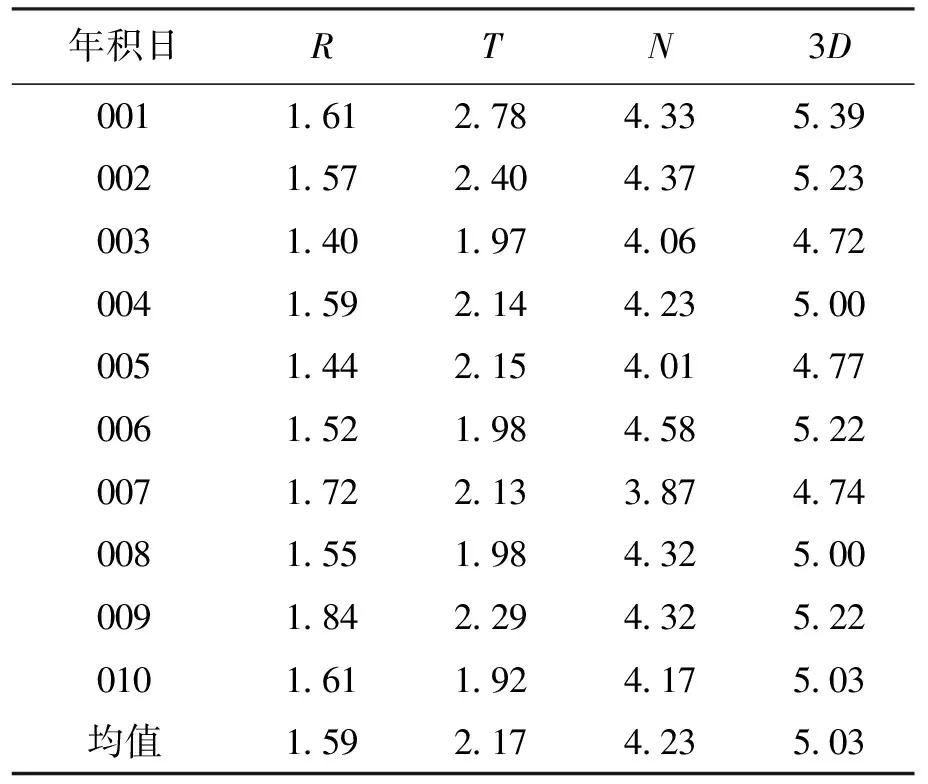
表3 GPS定轨结果与JPL事后精密轨道对比RMS统计

3.2外符合精度

3.2.1 SLR检核

目前多数低轨卫星均搭载SLR反射器,作为独立的轨道检验手段,且测距精度优于1 cm,因此可视为最重要的轨道评估方法。利用SLR观测数据检核低轨卫星轨道时,可分为两类统计,一是通过统计不同SLR台站的检核结果评估轨道的视向精度,二是通过整体残差获得轨道的视向精度。

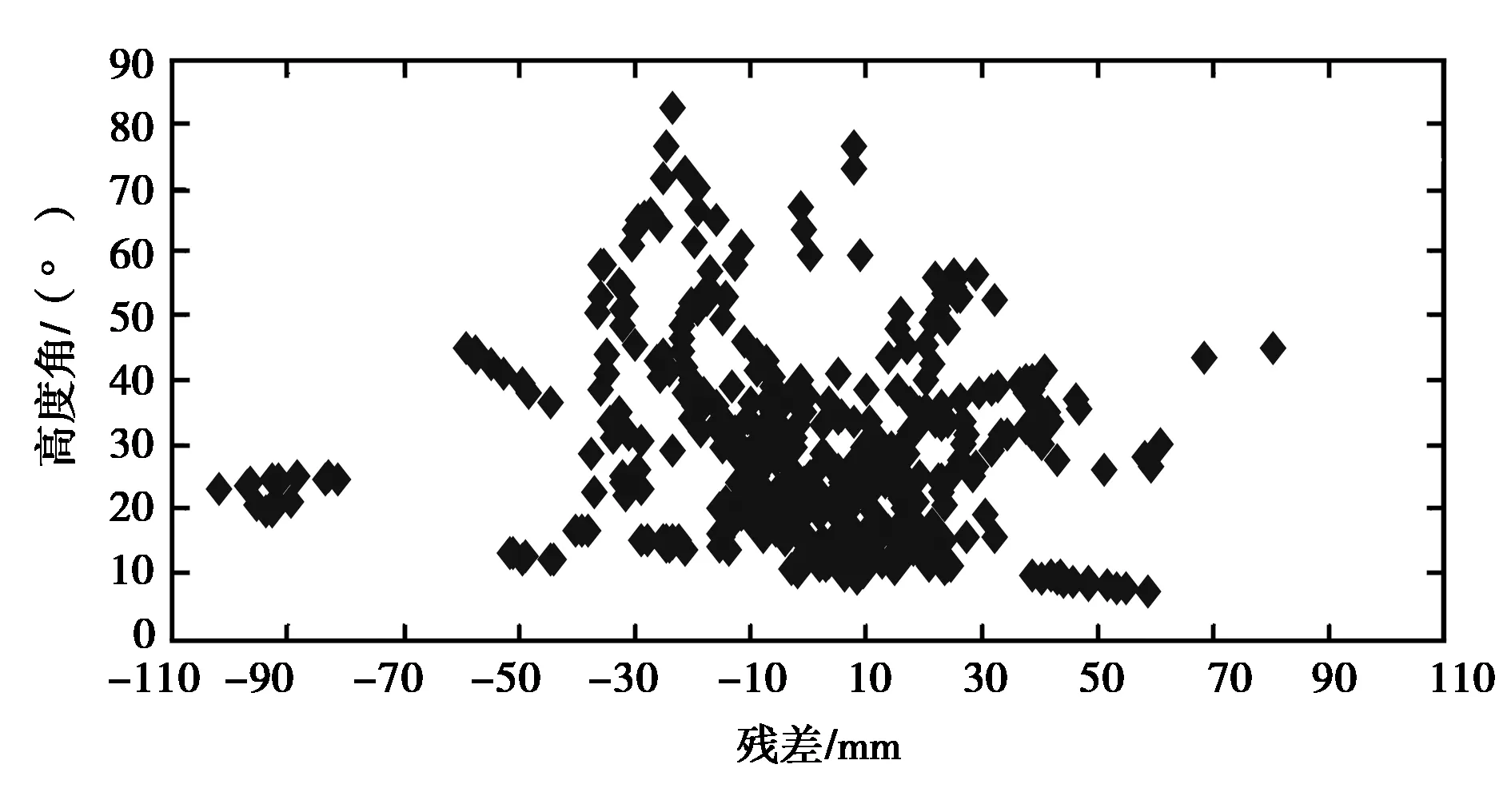
图7 JPL事后精密轨道SLR检核残差与高度角的关系

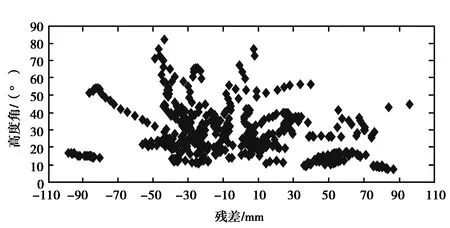
图8星载GPS精密轨道SLR检核残差与高度角的关系

图7示出了JPL事后精密轨道的SLR检核残差分布,视向残差较多分布在-30 mm至30 mm之间,高度角10°至30°内分布较多,随着高度角增大,残差点数越少,残差越小,精度越高。图8示出了本文星载GPS精密轨道的SLR检核残差分布,视向残差分布较为分散,基本符合残差随高度角变化的一般规律,可见JPL事后精密轨道的拟合效果较好。由表4,表5看出JPL事后精密轨道和本文的GPS定轨产品精度分别为2.84 cm和3.92 cm.JPL事后精密轨道径向精度优于3 cm,本文GPS定轨产品优于4 cm,但相比JPL结果,本文的SLR检核的GPS精密轨道的残差较为发散,均值稍大一些。

表4不同SLR台站数据检核精度统计RMS/cm

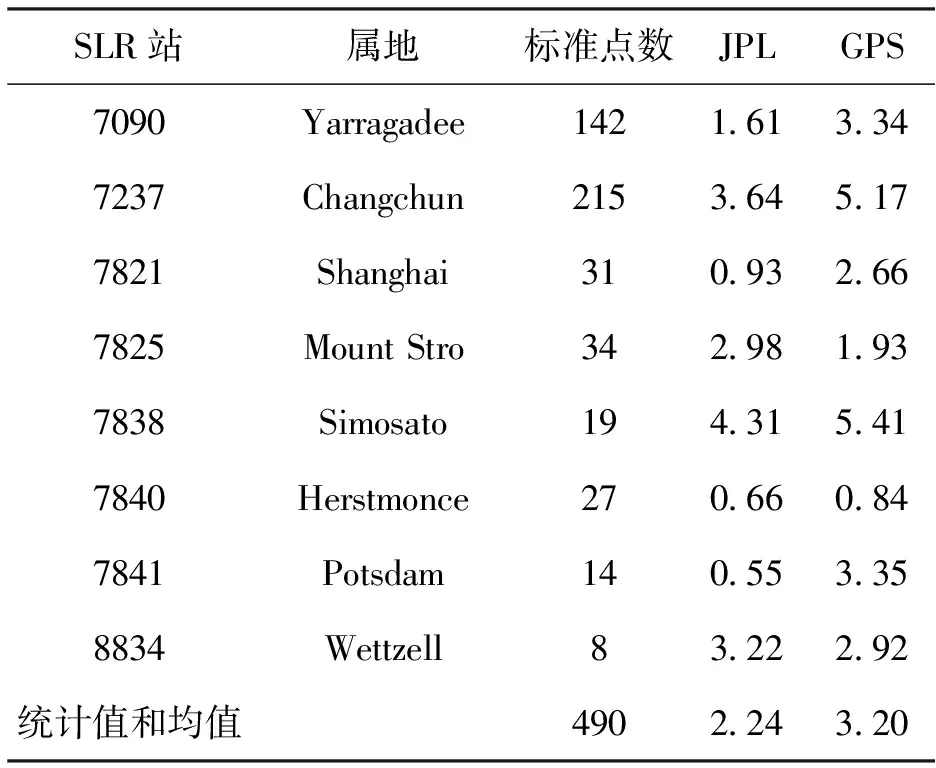
SLR站属地标准点数JPLGPS7090Yarragadee1421 613 347237Changchun2153 645 177821Shanghai310 932 667825MountStro342 981 937838Simosato194 315 417840Herstmonce270 660 847841Potsdam140 553 358834Wettzell83 222 92统计值和均值4902 243 20

表5 SLR检核轨道视向精度统计/cm

3.2.2 K波段测距检测

通过处理GRACE-A,GRACE-B星载GPS数据,获取两颗卫星轨道,进而与GFZ公布的Level1B中KBR1B数据进行对比,两者差值的标准差在18～25.3 mm,平均为21.8 mm,说明定轨结果可靠，如图9所示。

图9 KBR检核残差STD统计

4 结束语

本文基于简化动力学定轨方法,利用GRACE星载GPS数据进行精密定轨,重点讨论了常用的评估定轨内外符合精度的方法。其中,SLR因为其测距的高精度和应用的广泛性,可作为重要的外符合精度检验手段,甚至是整体精度评估标准。若可获取外部精密科学轨道,则外部轨道对比可视为评定内符合精度的重要方法,此外,轨道的重叠弧段检核也是重要的内符合精度检核手段。相关科研人员可依据LEO具体搭载设备和数据观测条件选择最佳的定轨精度评定方法,这对我国后续开展更为广泛的LEO卫星定轨研究具有借鉴意义。

[1] GUO J, ZHAO Q L, GUO X,etal. Quality assessment of onboard GPS receiver and its combination with DORIS and SLR for Haiyang 2A precise orbit determination[J]. Science China Earth Sciences, 2015, 58(1):138-150.

[2] 赵春梅,唐新明.基于星载GPS的资源三号卫星精密定轨[J].宇航学报, 2013, 34(9): 1202-1206.

[3] 汪楚,胡小工,郭鹏. 利用Bernese5.0软件实现LEO卫星精密定轨[J]. 天文研究与技术, 2011, 8(3):255-261.

[4] 秦建,郭金运,孔巧丽,等. Jason-2卫星星载GPS数据cm级精密定轨[J]. 武汉大学学报(信息科学版), 2014, 39(2):137-141.

[5] VEHLA D,ROTHACHER M. Kinematic and reduced-dynamic precise orbit determination of low earth orbiters[J]. Advance in Geoscience,2003, 1(1):47-56.

[6] 周晓青,胡志刚,张新远. 低轨卫星星载GNSS精密定轨的精度检核方法[J]. 武汉大学学报(信息科学版), 2010, 35(11):1342-1345.

[7] 赵齐乐,刘经南,葛茂荣,等. CHAMP卫星cm级精密定轨[J]. 武汉大学学报(信息科学版), 2006, 31(10):879-882.

[8] 黄观文,张睿,张勤,等. BDS卫星天线相位中心改正模型比较[J]. 大地测量与地球动力学, 2015, 35(4):658-661.

[9] 秦显平,焦文海,程芦颖,等. 利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报(信息科学版), 2005, 30(1):38-41.

[10] 彭冬菊,吴斌. 非差和单差LEO星载GPS精密定轨探讨[J]. 科学通报, 2007, 52(6):715-719.

[11] GU D, LAI Y, LIU J,etal. Spaceborne GPS receiver antenna phase center offset and variation estimation for the Shiyan 3 satellite[J]. Chinese Journal of Aeronautics, 2016, 29(5):1335-1344.

[12] 胡志刚,赵齐乐,郭靖,等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(s1):34-38.

[13] 李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995:189-190.

[14] KANG Z, TAPLEY B, BETTADPUR S,etal. Precise orbit determination for the GRACE mission using only GPS data[J]. Journal of Geodesy, 2006, 80(6):322-331.

[15] BERTIGER W, BAR-SEVER Y, DESAI S,etal. GRACE: Millimeters and Microns in Orbit[C]//ION GPS,Poland,2002.

ResearchonOrbitAccuracyEvaluationMethodsforLEOSatellitePrecisionOrbitDetermination

YUANJunjun,MENGRuizu

(CollegeofGeodesyandGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China)

Centimeter precision satellite orbit is a prerequisite for completing the science, commercial and other tasks undertaken by LEO satellites, in which post-fit orbit accuracy assessment is one important part of the task. According to observation conditions and carried equipments, selectingappropriate accuracy assessment methods is helpful to evaluate the orbit determination result objectively and accurately. This paper takes GRACE for example, discusses the accuracy of internal and external assessment methods, and gets useful conclusions for the follow-up to China's domestic satellite precision orbit mission.

LEO; precision orbit determination; accuracy evaluation; internalandexternal accuracy

10.13442/j.gnss.1008-9268.2017.05.002

P228.4

A

1008-9268(2017)05-0010-06

2017-08-04

联系人: 袁俊军 E-mail: 1558755464@qq.com

袁俊军(1991-),男,山东临沂人,硕士研究生,研究方向为低轨卫星精密定轨。

孟瑞祖(1991-),男,甘肃武威人,硕士研究生,研究方向为变形监测理论与应用。