三轮全转向叉车的转向控制策略研究

肖祖勋, 肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

三轮全转向叉车的转向控制策略研究

肖祖勋, 肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

文章以三轮全转向叉车转向系统的转向性能为研究对象,以线控转向系统整车二自由度模型为基础,结合叉车自身特点与转向要求,提出了前后轮等角反向转动控制、横摆角速度反馈控制2种控制策略。根据TFC20全向前移式电动叉车的实际数据,给出了基于车速、车轮转角的三轮全转向叉车转向系统性能的仿真对比分析。仿真结果表明,前后轮等角反向转动控制有效改善了传统三轮叉车机动性能,提高了叉车操纵灵活性;横摆角速度反馈控制有效改善了传统三轮叉车的横向稳定性,提高了叉车操纵稳定性。

三轮线控转向;等角反向转动控制;横摆角速度反馈;解耦

0 引 言

叉车多用于仓储物流中心搬运及装卸作业,有自己独特的作业要求,对于转向特性比其他车辆更高。由于叉车本身自重较大,而且负载变化较大,若转向时车速过大,在侧向力的作用下叉车容易失去行驶稳定性,发生侧滑或侧翻事故,相反叉车行驶速度过于缓慢的话,则会延长搬运时间,不利于运输的经济性[1-2]。另外,叉车在室内作业时还会遇到空间狭小的情况,因此对叉车的机动灵活性要求较高。

目前国内以汽油、柴油为主要燃料的传统内燃叉车正面临着严峻的考验,电动叉车以其环保和高性能的优势正处于蓬勃发展之中。传统三轮叉车都是后轮机械转向,无法主动控制前轮的转向,本文将三轮全转向技术与线控转向系统相结合,取消了传统转向盘和转向轮之间的机械连接,通过电信号传递控制信号,使转向盘与叉车转向轮之间的关系(角传递特性)摆脱机械系统的限制而自由设计[3-4],因此线控转向控制技术与三轮全转向技术在三轮电动叉车上的结合势在必行。

1 建立三轮全转向系统动力学模型

本文研究的是三轮全转向叉车模型,有2个前轮和1个后轮,转向系统分为前轮转向和后轮转向2个部分。

1.1 叉车转向模式

对于传统的三轮后轮转向叉车转向时,叉车后轮主动提供转向,前轮随动转向,根据文献[5]提出的转向模型,叉车的瞬时转向中心位于2个前轮的延长线上,如图1所示。

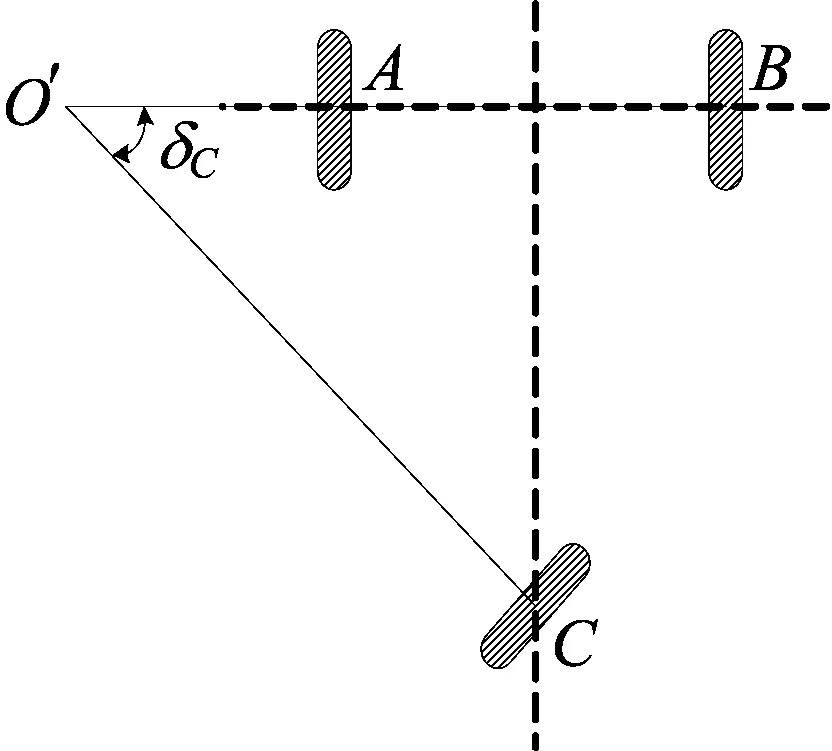
图1 传统后轮转向三轮叉车转向模式

而对于三轮全转向叉车转向系统而言,其转向模式主要有2种,如图2所示。

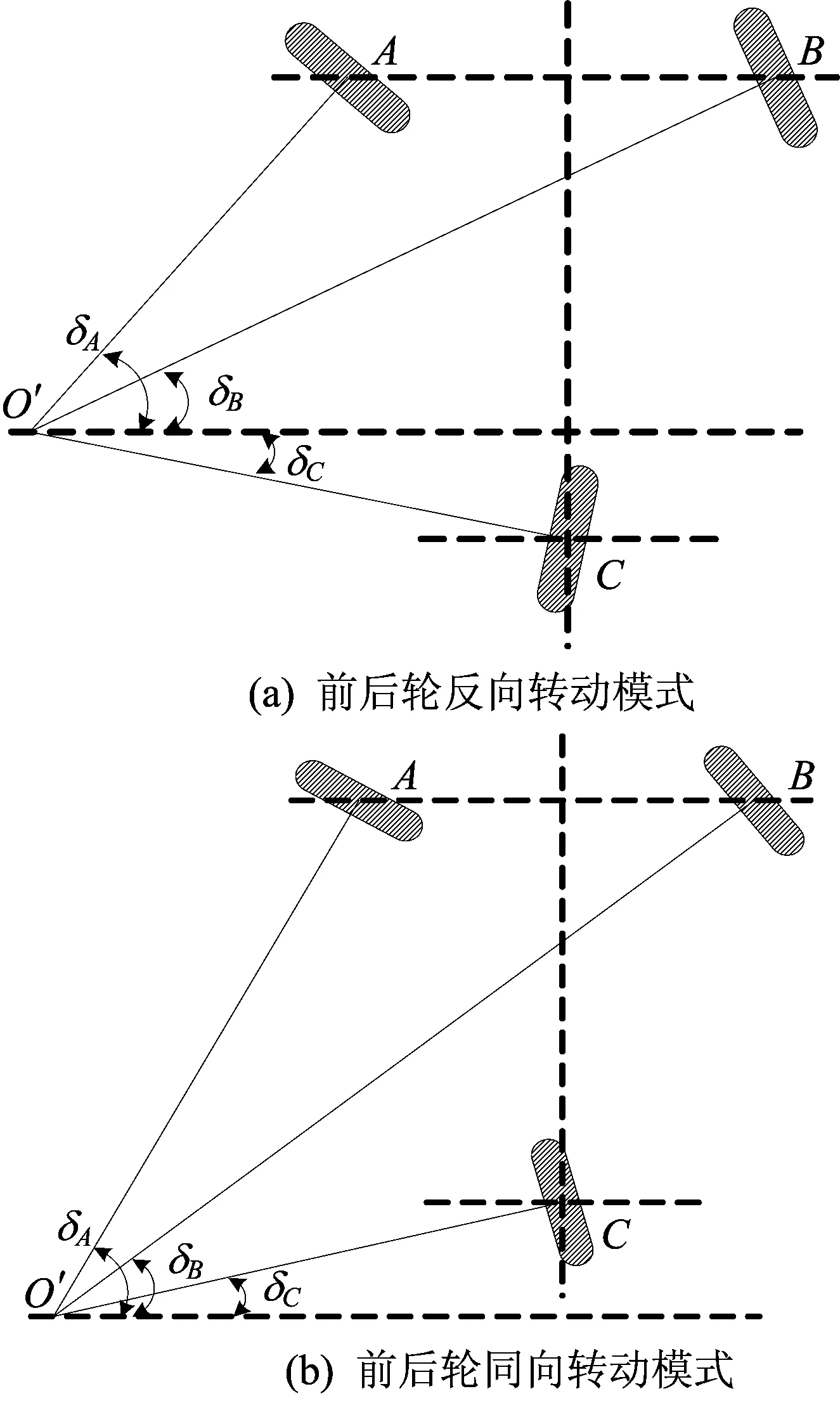
图2 三轮全转向叉车转向系统转向模式

图2a所示为前后轮反向转动模式,当叉车低速转向行驶时,2个前轮与后轮的转向角是相反的,与传统的前轮转向叉车相比,能使叉车的转向半径变小,提高叉车的低速机动性,于转向空间狭小的搬运场地而言意义重大。图2b所示为前后轮同向转动模式,当叉车转向行驶速度较快时,后轮转向角与前轮转向角保持同向,能够有效避免叉车发生过度转向的可能,从而提高叉车转向稳定性。

1.2 叉车前后轮转向角关系分析

本文研究的叉车是三轮全转向叉车,因此本文将在传统分析模型的基础上进行扩展,以向左转向的叉车为研究对象,三轮全转向叉车分析模型如图3所示。

图3 三轮全转向叉车分析模型

叉车在实际作业中,行驶速度在变化,转弯转过的角度也在变化,3个车轮的转向角也将处于不断的变化之中。为了更好地研究车轮转向角和叉车参数的关系,本文在2个前轮连线中点处虚构出了1个前轮M,称之为虚构前轮M。

首先介绍图3中和车轮转角相关的叉车参数:δi(i=A,B,C,M) 分别为左前轮、右前轮、后轮和虚拟前轮的转向角;a、b分别为叉车质心到叉车前后轴的水平距离;L为叉车前后轴间的距离;W为叉车前轮间的距离;O′为瞬心转动中心;RO为由O′点至质心O点的距离即质心转向半径;D为叉车转向中心到叉车前轴的水平距离;R为叉车转向中心到叉车虚拟前轮与后轮连线上的距离。

由图3中所示的几何关系得到三轮转向叉车各轮转向角与叉车参数之间的关系式为:

(1)

经过运算,由(1)式可以得到:

(2)

因此通过车轮转角和叉车参数可以得到叉车的质心转向半径为:

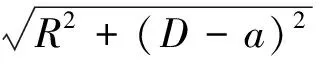
(3)

1.3 叉车控制模型的建立

首先介绍图3中和叉车控制模型相关的参数:m为叉车自重;Fi(i=A,B,C) 分别为地面作用于左前轮、右前轮、后轮上的侧向力;αi(i=A,B,C) 分别为叉车的左前轮、右前轮和后轮的轮胎侧偏角;vI为质心的运动速度;v为叉车质心的侧向速度;u为叉车质心的纵向速度;ωr为叉车绕质心的横摆角速度;β为叉车的质心侧偏角。

设叉车得到驾驶员指令,各轮转角分别为δi(i=A,B,C)车轮转动时在质心产生离心力,其在前后轮上引起侧向反作用力为Fi(i=A,B,C),引起相应的侧偏角为αi(i=A,B,C)。

质心速度的约束关系为:

vI=ωrRO

(4)

其中,vI在y轴上分量为u=vIcosβ。

由于车辆转向时侧偏变化量极小,成渐变变化,非瞬时变化,在转向瞬间cosβ的值可视作1,u=vI=ωrRO。vI在x轴上的分量为:

(5)

若质心在x轴处的加速度记为ac,则有:

(6)

根据牛顿第二定律,由图3可以写得叉车沿x轴的力平衡方程和在xy平面的横摆运动的力矩平衡方程,即通常所指的线性二自由度模型的动力学方程式:

(7)

其中,Iz为叉车的横摆惯量。

轮胎侧向力与轮胎侧偏角呈现的是非线性关系,但在一般情况下叉车转向过程中轮胎的侧偏角足够小,本文把轮胎侧向力和轮胎侧偏角之间的关系视为线性,采用的近似线性模型为:

Fi=Kiαi,i=A,B,C

(8)

其中,Ki(i=A,B,C)分别为叉车的左前轮、右前轮和后轮的轮胎侧偏刚度。叉车各轮的轮胎侧偏角为:

(9)

车辆转向时各轮的转向角度呈渐变变化,非瞬时变化,在转向瞬间cosδi的值可视作1,由(7)～(9)式可以推得线性二自由度模型的动力学方程为:

(10)

2 控制策略

横摆角速度、质心侧偏角和转向半径是衡量叉车转向性能的重要因素。一般情况下,转向过多是由于后轮侧向力太小引起的,此时转弯半径比驾驶员期望的要小,叉车将会产生较大的横摆角和质心侧偏角,驾驶员将很难控制叉车的转向。转向不足则通常是由于前轮侧向力太小引起的,转弯半径要比驾驶员期望的要大,叉车很难跟随预期的轨迹[6-7]。为了唯一确定某一时刻各车轮转角,本文采取2种不同的控制策略对其进行控制,并将其和传统后轮转向控制方法进行比较。

2.1 前后轮等角反向转动控制策略

这是一种根据叉车驾驶员驾驶经验总结出来的控制策略,名称中的等角反向转动指的是虚拟前轮转角和后轮转角大小相等方向相反,如图4所示。

由图4可得如下计算公式:

(11)

由(1)式、(2)式和(11)式可以得到叉车转角之间的关系为:

(12)

通过(3)式、(11)式可以得到叉车质心转向半径为:

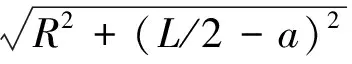
(13)

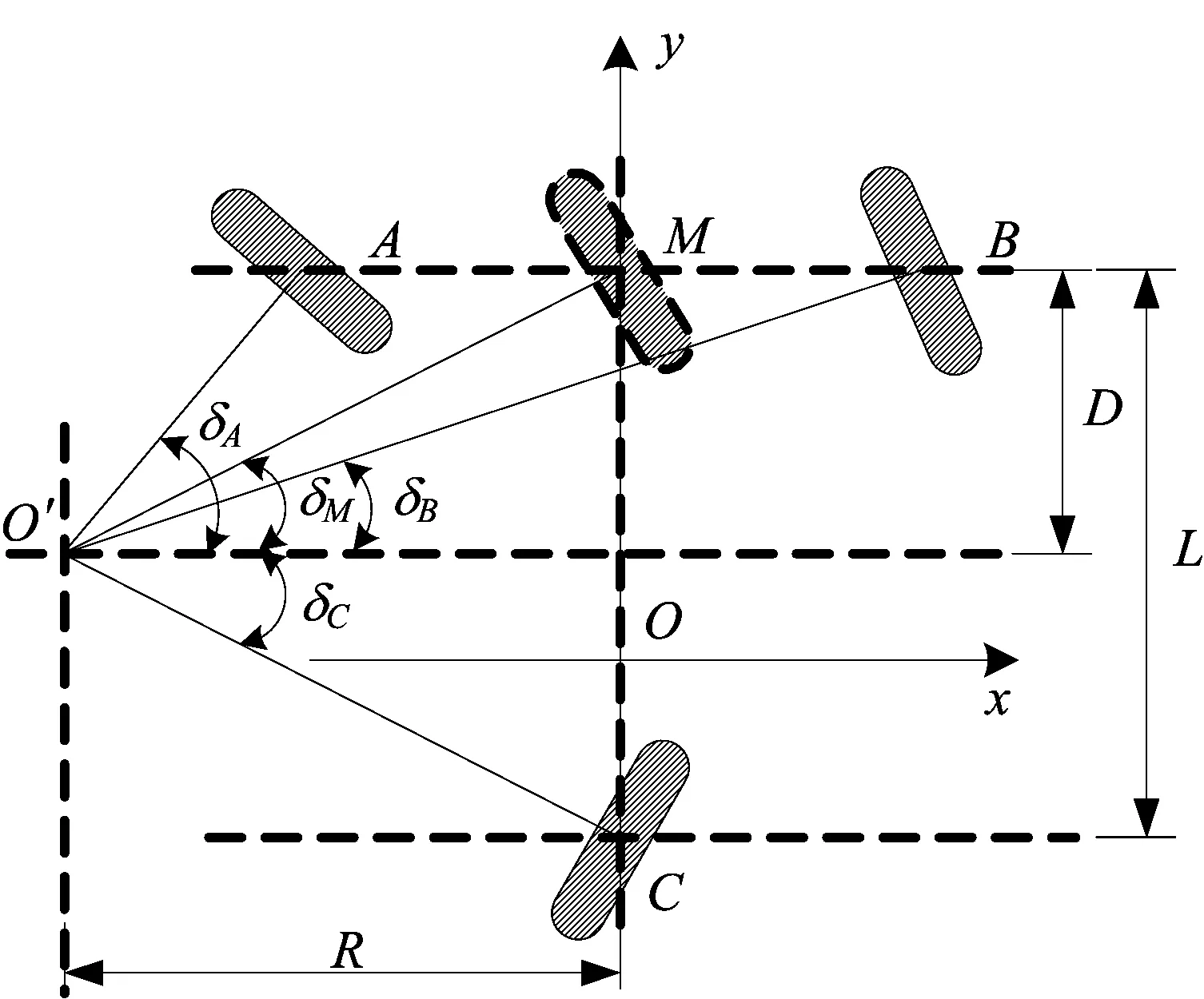
图4 前后轮等角反向转动模式

从图4中可以看出,叉车瞬时转动轴中心位于车体纵向中心所在的水平线上,与传统的前轮转向叉车相比,这能使叉车的转向半径变小,提高叉车的机动灵活性,这是前后轮等角反向转动控制策略的一大优点。

2.2 横摆角速度反馈控制策略

对于进行转向动作的叉车而言,决定其转向稳定性高低的一个重要指标是质心侧偏角[8]。若通过控制算法质心侧偏角能够降为0[9],这将使得叉车的转向稳定性大大提高,下文研究的横摆角速度反馈控制策略能够较好地解决该问题。

为了更好地研究横摆角速度反馈控制策略,本文将动力学方程(10)式写成如下形式:

(14)

(15)

将(15)式代入(14)式，得到后轮横摆角速度反馈三轮转向的转向模型为:

(16)

质心侧偏角与横摆角速度解耦前叉车转向系统的传递函数为二阶,无法独立控制质心侧偏角与横摆角速度。质心侧偏角与横摆角速度解耦后,质心侧偏角的动力性为稳定的一阶系统,(16)式中由于Iz的值远远大于aKA+aKB-bKC的值,得(aKA+aKB-bKC)/Iz≈0,可以忽略质心侧偏角对横摆角速度的影响,横摆角速度也为一阶系统,只受各车轮转角的影响。

对叉车后轮进行横摆角速度反馈控制的缺点是其可能导致叉车转向不足,为改善这一缺点,本文对虚拟前轮也进行横摆角速度反馈[10],即

δM=δin-Gωr

(17)

其中,δin为虚拟前轮转角输入;G为横摆角速度反馈系数。

由(1)式、(2)式可以得到2个前轮转角与虚拟前轮转角的关系为:

(18)

横摆角速度反馈系数G与系统快速性、稳定性有关,适当调整G的大小可以改善叉车转向的稳定性和快速性。

3 仿真结果及分析

为了验证本文提出的转向控制策略,本文根据TFC20全向前移式电动叉车的实际数据,基于 Matlab进行了仿真。整车自重m=5 000 kg,质心到前轴距离a=1.408 m,质心到后轴距离b=0.512 m,叉车前后轴间的距离L=1.92 m,2个前轮之间的距离W=1.88 m,左前轮、右前轮和后轮的轮胎侧偏刚度KA、KB和KC分别为77 850、77 850、15 3840 N/rad,横摆惯量Iz=11 216 kg·m2。

叉车正常行驶速度在0～15 km/h范围内,本文选择车速为10 km/h,并输入初始值为0、斜率为 0.2 rad/s、斜坡上升时间为1 s的方向盘转角信号。

转向特性仿真之前,首先进行的是横摆角速度反馈控制中横摆角速度反馈系数G的选择。通过观察不同反馈系数G时横摆角速度的响应变化,选择最佳的横摆角速度反馈系数G,如图5所示。

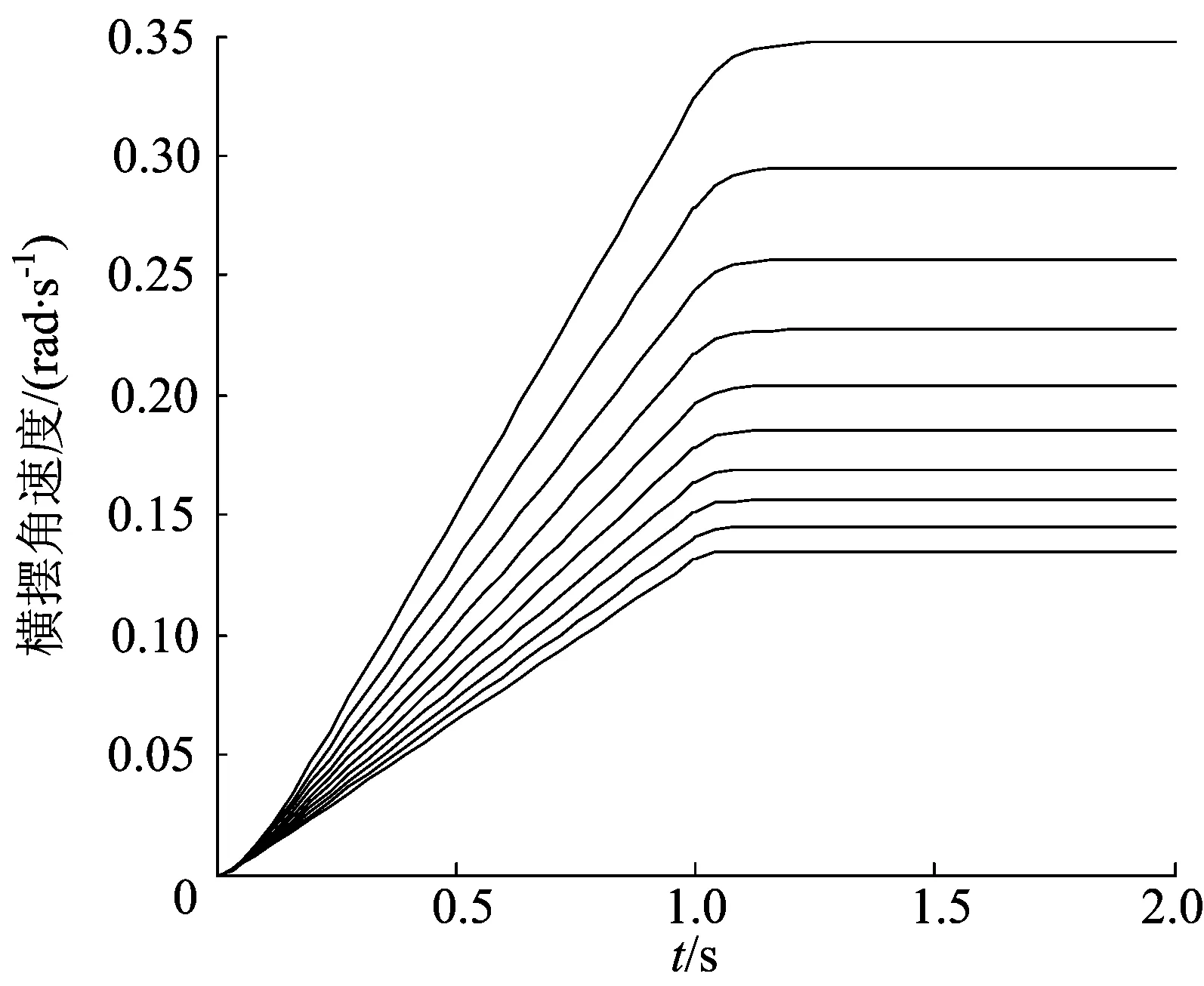
图5 不同反馈系数的横摆角速度响应

图5中从上到下依次为G=0.1，0.2,…,1,可以看到随着G值增大,横摆角速度反馈作用增强,横摆角速度稳定值减小。在以上车速和转角条件下,本文选定横摆角速度稳定时的参考值为0.23 rad/s,过大或过小的横摆角速度将导致叉车的过多转向或不足转向。本文选择最接近参考值时的G,得到叉车车速为10 km/h下最佳的横摆角速度反馈系数G=0.389,此时横摆角速度稳定值为 0.230 2 rad/s。

在以上基础上,本文进行三轮全转向叉车在传统后轮转向、前后轮等角反向转动控制、横摆角速度反馈控制时系统转向性能仿真的比较和分析,3种控制方法下质心侧偏角、横摆角速度响应的仿真结果如图6所示。

在整个仿真时间0 ～2 s内,在横摆角速度反馈控制下质心侧偏角稳态值一直保持非常小,接近于0,这是后轮进行横摆角速度反馈的优点。在传统后轮转向、前后轮等角反向转动控制下,从图 6a中可以看出,质心侧偏角经过 1 s 后逐渐达到稳定值。两者相比,前后轮等角反向转动控制策略下质心侧偏角响应速度更快,质心侧偏角稳定值也更小,可见在前后轮等角反转控制方法下叉车的侧偏情况也有一定的改善。

对于图6b中的横摆角速度而言,从数值方面来看,横摆角速度稳定值的参考值为 0.23 rad/s,传统后轮转向控制策略的横摆角速度稳定值为 0.27 rad/s,前后轮等角反向转动控制策略的横摆角速度稳定值为 0.41 rad/s,横摆角速度反馈控制策略的横摆角速度稳定值为 0.23 rad/s,明显可以看出,进行横摆角速度反馈控制之后的横摆角速度值比传统后轮转向控制更接近参考值,得到了预定的控制效果。另外,从响应速度方面来看,横摆角速度反馈控制下响应速度更快,横摆角速度反馈控制策略在快速性上有很大优势。

图6 3种控制方法下质心侧偏角、横摆角速度响应对比

本文在相同的条件下进行3种控制方法下转向半径仿真,结果如图7所示。

从图7可以看出,传统后轮转向控制下转向半径经过1 s 后变为9.7 m,并保持稳定。前后轮等角反向转动控制下转向半径经过 1 s 后变为4.8 m,并保持稳定。横摆角速度反馈控制下转向半径经过 1 s 后变为11.8 m,并保持稳定。对比来看,前后轮等角反向转动控制下转向半径减小达到50%,这对某些地方相对狭窄,而叉车必须进行转向的情况而言,无疑是有很大优势的。

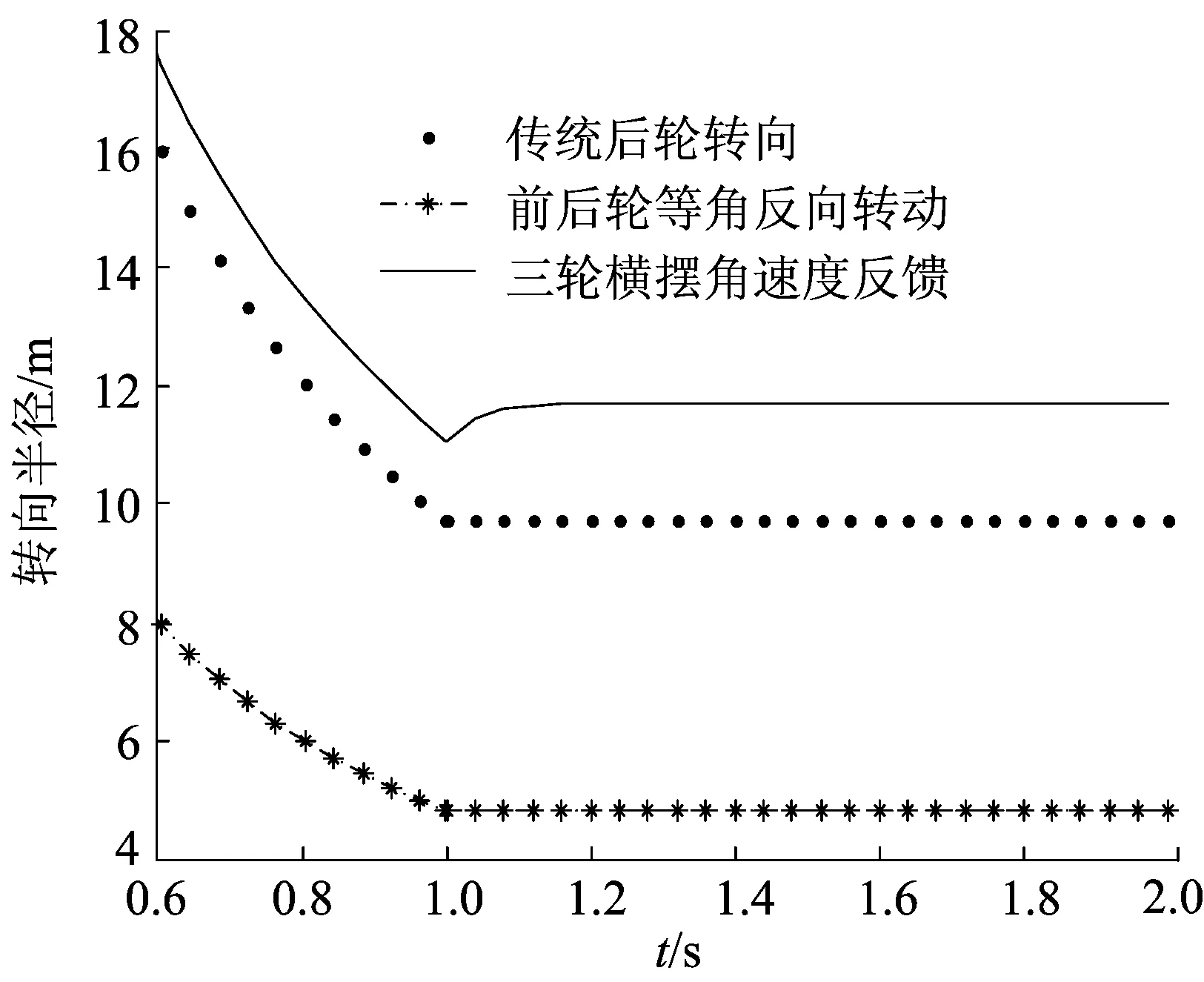
图7 3种控制方法下的转向半径响应对比

综合以上分析可以得知,横摆角速度反馈控制策略通过调整横摆角速度反馈系数G来获得期望的横摆角速度稳定值,将质心侧偏角和横摆角速度控制在理想的范围内,这样就使得叉车的横向稳定性得到提高;而在前后轮等角反向转动控制下,虽然叉车转向的横摆角速度未得到很好的改善,但是质心侧偏角有所改善,而且在转向半径上呈现了巨大的优势。

4 结 论

本文通过对二自由度整车模型下三轮全转向叉车转向系统转向性能的研究,提出了基于车速、车轮转角的前后轮等角反向转动控制、横摆角速度反馈控制2种控制策略。仿真结果表明,前者达到了降低转弯半径的目的,提高了机动性能,控制了叉车的运动轨迹;后者解耦横摆和侧偏运动,改善了叉车操纵稳定性。

[1] LEMERLE P,HOPPNER O,REBELLE J.Dynamic stability of forklift trucks in cornering situations: parametrical analysis using a driving simulator[J].Vehicle System Dynamics,2011,49(10):1673-1693.

[2] RACHID A,RODOLFO O,MICHEL B.Combined longitudinal and lateral control for automated vehicle guidance[J].Vehicle System Dynamics,2014,52(2):261-279.

[3] 吴佳楠,肖本贤.基于模糊控制的叉车线控转向系统变传动比研究[J].合肥工业大学学报(自然科学版),2014,37(8):912-915.

[4] 于蕾艳,林逸,施国标.四轮线控转向系统的转向控制策略研究[J].计算机仿真,2008(4):278-281.

[5] ACKERMANN J,ODENTHAL D,BUNTE T.Advantages of active steering for vehicle dynamics control[C]//Proceedings of 32nd ISATA,Automotive Mechatronics Design and Engineering,1999:263-270.

[6] 宋宇,陈无畏,陈黎卿.四轮转向车辆横摆角速度反馈与神经网络自适应混合控制的研究[J].汽车工程,2013,35(1): 66-71.

[7] 杨胜兵.线控转向系统控制策略研究[D].武汉:武汉理工大学,2008.

[8] GOODARZI A,ESMAILZADEH E.Design of a VDC system for all wheel independent drive vehicles[J].IEEE/ASME Transactions on Mechatronics,2007,12(6):632-639.

[9] WHITEHEAD J C.Four-wheel steering: maneuverability and high speed stabilization：SAE Technical Paper No.980642[R].,1998.DIO：10.4271/880642.

[10] 于蕾艳,林逸,施国标.线控转向系统的主动转向控制策略[J].农业机械学报,2008,39(1):4-6.

Researchonall-wheelsteeringcontrolstrategyforthree-wheelforklift

XIAO Zuxun, XIAO Benxian

(School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)

Taking the steering performance of all-wheel steering system for the three-wheel forklift as the research object, based on a 2-DOF model of three-wheel steer-by-wire system, and in view of the characteristics and steering requirements of forklift, two kinds of control strategies are proposed, one does the isometric reverse rotation at front and rear wheel, and the other uses the yaw rate feedback. According to the actual data of the forklift TFC20, the simulation analysis of the steering performance of all-wheel steering system for the three-wheel forklift based on speed and wheel angle is given. The simulation results show that compared with the traditional steering control method, the first control strategy improves the steering flexibility of the forklift, and the second control strategy improves the steering stability of the forklift.

three-wheel steer-by-wire; isometric reverse rotation control; yaw rate feedback; decoupling

2016-02-26；

2016-03-18

国家自然科学基金资助项目(61304007)

肖祖勋(1992-),男,江西赣州人,合肥工业大学硕士生; 肖本贤(1964-),男,安徽合肥人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.10.010

TP13

A

1003-5060(2017)10-1349-06

(责任编辑 张 镅)