正交Hermite-Padé表中沿对角递推公式
陶长虹, 夏迎春, 褚 标
(1.合肥工业大学 数学学院,安徽 合肥 230009; 2.安庆市石化第一中学,安徽 安庆 246001)
正交Hermite-Padé表中沿对角递推公式
陶长虹1, 夏迎春2, 褚 标1
(1.合肥工业大学 数学学院,安徽 合肥 230009; 2.安庆市石化第一中学,安徽 安庆 246001)
文章首先建立了正交多项式序列中任意两项乘积的公式,然后在正规性条件下,在s维正交H-P (Hermite-Padé)表中沿对角线递推地构造正交H-P多项式序列,解决了正交H-P多项式的计算问题,并给出了余项估计式。
正交多项式;唯一性;Hermite-Padé逼近;Hermite-Padé表;对角递推公式
0 引 言
Hermite-Padé(H-P)逼近是利用函数的形式级数对函数在原点附近进行逼近[1-7];正交H-P逼近是对函数的正交多项式展开式在区间上进行的整体逼近[8-12],两者都有较重要的理论意义。
建立正交H-P逼近多项式表中的递推关系对于正交H-P多项式的计算有着重要的意义。文献[13]给出了正交H-P多项式表中的恒等式及相邻页面间的关系。本文给出在正交H-P多项式表中沿对角线的递推关系,由此关系可计算正交H-P多项式表。
1 引 理
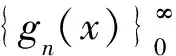
gn(x)=(x-an)gn-1(x)-bngn-2(x)
(1)
其中
g0(x)=1,g1(x)=x-a1;
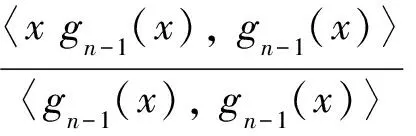
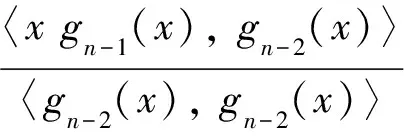
n=1,2,…
(2)
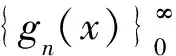
M=max{m,n},N=min{m,n},
则
(3)
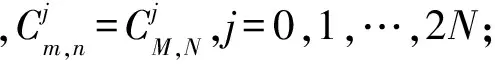
(4)
当N≥2时,可递推计算出。
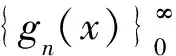
(5)

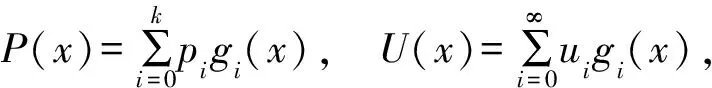
P(x)U(x)=
(6)
2 定 义
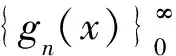
给定正交级数展开式
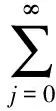
其中,s为大于1的整数,则称U=(U1(x),U2(x),…,Us(x))为级数组。
给定向量L=(l1,l2, …,ls),li≥-1, 为整数且L中至少有一个分量非负。
定义1 设P1(x),P2(x),…,Ps(x)分别为次数不超过l1,l2, …,ls的广义多项式,li为整数且li≥-1(若li=-1,则Pi(x)≡0)。若P1(x),P2(x),…,Ps(x) 不全恒为0且
(7)
则称Φ(L)=(P1(x),P2(x),…,Ps(x))为U的L型正交H-P多项式(orthogonal Hermite-Padé polynomial,OHPP)。记
R(x)=O(gλ(L)(x))=cλ(L)gλ(L)(x)+…。
(8)
由推论2及(7)式或(8)式可得到一个含有P1(x),P2(x),…,Ps(x)、λ(L)+1个未知数、λ(L)个线性齐次方程的方程组。该方程组一定有非零解,即P1(x),P2(x),…,Ps(x)(即Φ(L))总存在。这样的解不唯一,因而Φ(L)不唯一,但在下面的正规性条件下它是唯一的[4]。
定义2 若级数组U对任何满足上述假设的向量L都有
Δ(L)=Δ(l1,l2,…,ls)=
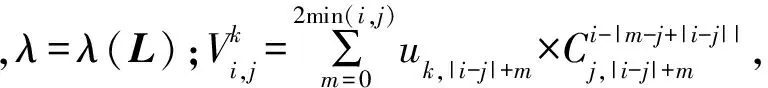
在下文中,总是假设U是正规的。
3 正交H-P表中沿对角递推公式
下面的递推关系是在s维正交H-P表中进行的。
令L-1=(-1,-1,…,-1),Lj=Lj-1+Ed,j=0,1,2,…,其中,Ed为s维单位向量,其中第d个分量为1,其余分量为0。并记Lj=(lj1,lj2, …,ljs)。
下面的定理1将在正交H-P表中以显示方式、递推地构造OHPP序列{Φ(Lj)}(j=0,1,…),其中,g(x)Φ(Lj)=(Pj1(x),Pj2(x), …,Pjs(x)), degPji=lji,i=1, 2, …,s。此外,若记
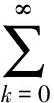
则
ord(Rj(x))=j,j=0,1,2, …
(9)
Φ(L0)=Ed0, 相应地有R0(x)=Ud0(x)。对于任意n> 0,利用已知的Φ(Lj)及相应的余项Rj(x)(j 在算法中,Φ(Ln)的第dn个分量必须满足degPn dn>degPj dn。定理1是最简便的一种方法:Φ(Ln)为向量(0,0,…,0,glndn(x), 0, …, 0)(第dn个分量不为0)及Φ(L0),Φ(L1),…,Φ(Ln-1)的线性组合。因为Φ(Ln)与向量(0,0,…,0,glndn(x),0,…,0)相乘的结果为glndn(x)×Udn(x)=udndn+…,所以由(7)式知,可以选择适当的组合系数,使得对应组合式中的余项Rn(x)满足ord(Rn(x))=n。 对任意n≥0,在表中可由(10)~(12)式计算Φ(Ln),由(13)式计算余项Rn(x),具体如下: (10) 其中,ln=ln dn; (11) (12) 余项Rn(x)的系数为: (13) 上述结论显然:由(10)式知,对任意αk,都有degPni≤lni,i=1,2,…,s; degPn dn=ln。由推论1,对应(Pn1(x),Pn2(x), …,Pns(x))的余项 (14) 其中,sdnk由(12)式给出;由(9)式、(11)式可依次消去Rn(x)中的g0(x),g1(x), …,gn-1(x)项,从而有ord(Rn(x))≥n。 下面的定理都假设Ln-1的各分量 ln-1, i≥0,i=1,2,…,s (15) 令m为满足下列条件的最大整数:m≤n-s,至多有一个Ln-Lm中的某个分量为0。 如果Ln-Lm中恰好存在为0的分量(记为第z个),那么一定存在整数m′、m″,满足m 定理1 若对任何j,m (16) 其中 j=m-1,m,…,n-1 (17) (18) (19) 证明由(19)式及假设知,m> 0。 首先根据引理1计算βjs′,γjs′,然后再用(16)~(19)式计算Φ(Ln)。 显然,当j (20) 第i(i=1,2,…,s,i≠dn)个分量的次数不超过相应的ln i,因此 注利用(16)~(19)式计算OHPP比较费时,但在ln=0时必须使用这些关系。当条件(16)式不满足时,可应用定理2。 定理2 若m>0,存在正整数i,m (21) αj由(17)式得到,此时有: 余项Rn(x)由(19)式确定。 证明排列U1(x),U2(x),…,Us(x)使z=1(即第Lm,Lm+1, …,Ln的第1个分量值相同),dj1=2,…,djq=q+1,dn=dn′=q+2。 而ljidn 因为Ln-1-Ln′的前q+2个分量为0,其余为正,所以对任何αj,(21)式右端的第k(k=1,2,…,s)个分量的次数都不超过lnk;当k=q+2时,等于lnk。按照(17)式选择αj即可使与Φ(Ln)对应的余式Rn(x)满足ord(Rn(x))≥n。证毕。 本文在s维正交H-P表中沿对角线递推地构造正交Hermite-Padé多项式序列,解决了正交Hermite-Padé多项式的计算问题,并给出了余项估计式。 [1] PASZKOWSKI S.Recurrence relations in Padé-Hermite approximation[J].J Comput Appl Math,1987,19:99-107. [2] BAKER G A,Jr,LUBINSKY D S.Convergence theorems for rows of differential and algebraic Hermite-PadéApproximation [J].J Comput Appl Math,1987,18(1):29-52. [3] PASZKOWSKI S.Hermite-Padé approximation (basic notions and theorems)[J].J Comput Appl Math,1990,32(1/2):229-236. [4] ASTAFYEVA A V,STAROVOITOV A P.Hermite-Padé approximation of exponential functions[J].Sbornik Mathematics,2016,207(6):769-791. [6] BUSLAEV V I,SURTIN S P.On equilibrium problems related to the zero distribution of Hermite-Padé approximation polynomials[J].Proceedings of the Steklov Institute of Mathematics,2015,290(1):256-263. [8] 徐献瑜,李家楷,徐国良.Padé逼近概论[M].上海:上海科学技术出版社,1980:248-289. [9] MANO T,TSUDA T.Hermite-Padéapproximation isomonodromic deformation and hypergeometric integral[J].Mathematische Zeitschrift,2017,285(1/2):397-431. [10] 法埃兹 阿赫买德.正交多项式及Padé逼近[J].应用数学和力学,1998,19(7):619-623. [11] 吴传生,周洋,黄小为.基于正交多项式下的数值微分任意阶稳定逼近[J].数学杂志,2015,35(2):397-406. [12] 罗瑞芬.基于Chebyshev正交多项式逼近理论的随机Hopf分岔的研究[D].兰州:兰州交通大学,2016. [13] 陶长虹.正交Hermite Padé中相邻页面间的递推关系[J].合肥工业大学学报(自然科学版),2006,29(11):1481-1484. [14] 切尼 E W.逼近论导引[M].上海:徐献瑜,译.上海科学技术出版社,1981:27-69. [15] 向隆万.正交多项式的积化和差公式[J].工程数学学报,1991,8(1):116-118. [16] 陶长虹.正交Hermite-Padé表中的恒等式[J].大学数学,2006,22(6):102-105. DiagonalrecursiveformulaonorthogonalHermite-Padétable TAO Changhong1, XIA Yingchun2, CHU Biao1 (1.School of Mathematics, Hefei University of Technology, Hefei 230009, China; 2.Anqing Shihua No.1 Middle School, Anqing 246001, China) The product formula of any two polynomials in an orthogonal polynomial sequence is first established. Under the condition of regularity, the orthogonal Hermite-Padé(H-P) form sequences are recursively constructed along the diagonal in thes-dimensional orthogonal H-P table. This solves the calculation problem of orthogonal H-P table. And the corresponding remainder estimation formula is given. orthogonal polynomial; uniqueness; Hermite-Padé approximation; Hermite-Padé table; diagonal recursive formula 2017-04-18; 2017-07-13 安徽省省级质量工程专业综合改革试点资助项目(2012zy007);名师工作室资助项目(2015msgzs126) 陶长虹(1963-),男,安徽无为人,合肥工业大学副教授;褚 标(1967-),男,安徽无为人,博士,合肥工业大学副教授,硕士生导师,通讯作者:E-mail:hfgdhbt@163.com. 10.3969/j.issn.1003-5060.2017.10.026 O174.41 A 1003-5060(2017)10-1437-04 (责任编辑 朱晓临)
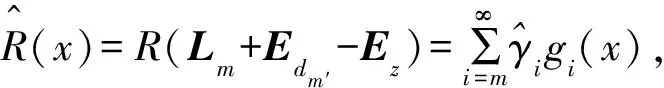
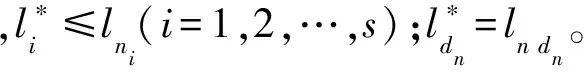
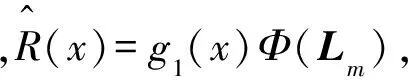
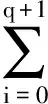
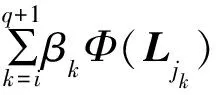
4 结 论