汽车制动控制系统ABS/EBD设计与仿真

王健，杨君，于蓬，郑金凤

1.山东交通学院汽车工程学院，山东济南 250357；2.山东明宇新能源技术有限公司，山东济南 271100

0 引言

汽车紧急制动，特别是在附着系数较低的路面上紧急制动时，汽车防抱死制动系统(anti-locked braking system,ABS)可以防止前后车轮抱死拖滑，在保证汽车具有转向功能的同时，防止汽车不发生甩尾侧滑等危险情况，保持汽车的制动稳定性，且可以缩短制动距离[1-3]。电子制动力分配(electronic brake force distribution，EBD)系统作为ABS的子系统，可以在车辆制动时控制制动力在各轮间的分配，更好地利用各轮的附着系数[4-11]。

国内大多数ABS采用逻辑门限值控制，通过大量试验确定各门限值，对系统的控制很不稳定[12-14]。本文ABS采用滑模变结构控制，该方法是针对非线性和参数不确定性系统的控制方法[15-17]，具有很好的鲁棒性。EBD系统采用模糊控制，该方法对系统中的参数变化、外界干扰、系统非线性等具有很强的鲁棒性。通过建立1/2车辆动力学模型、设计基于滑模变结构控制的ABS控制器和基于模糊控制的EBD控制器，在不同路面上进行ABS/EBD系统的仿真验证，以期提高车辆的制动性能。

1 车辆动力学模型

为了设计ABS、EBD控制器以及进行系统动力学仿真，需建立车辆动力学模型。为便于建模，对车辆动力学模型进行简化：1)忽略路面不平度的影响；2)忽略空气阻力和轮胎滚动阻力；3)忽略传动系、转向系和悬架系统的影响；4)假设汽车只有纵向运动，无侧向和垂直方向运动。

建立1/2车辆动力学模型，如图1所示，车辆参数如表1所示。

图1 车辆动力学模型

表1 车辆参数

a/mb/mhs/mhf/m1.1861.2580.60.3hr/mmf/kgmr/kgms/kg0.3961191285

图1中：a、b分别为质心至前、后轴的距离，hs为簧上质量质心高度，hf、hr分别为前、后簧下质量质心高度，mf、mr分别为前、后簧下质量，ms为车辆簧上质量，Fzf、Fzr分别为地面对前、后轮的垂直载荷，Ftf、Ftr分别为前、后轮的地面制动力。

由车辆动力学模型可得：

(1)

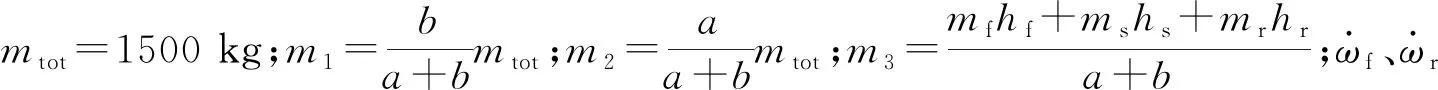
基于滑模变结构控制的ABS的主要控制目标为前、后车轮的滑移率

(2)

式中ωf、ωr分别为前、后轮的角速度。

2 ABS滑模变结构控制器设计

为了提高控制器的鲁棒性，采用滑模变结构控制设计ABS控制器。滑模变结构通过控制汽车前后轮的制动力矩[18-19]，使汽车前后轮滑移率跟踪理想滑移率，保持车轮滑移率在最佳滑移率附近，从而充分利用路面附着系数[20-21]。首先定义滑模变结构控制的车轮滑移率跟踪误差

(3)

式中：S1、S2分别为前后轮滑移率跟踪误差；λfd、λrd分别为前、后轮理想滑移率。

令

(4)

(5)

(6)

对式(3)两边分别求导数，并令S1、S2的导数为0，结合式(1)可以得到前后轮等效控制制动力矩

(7)

由式(4)知：当μf=μr=1时，f1取最小值；当μf=μr=0时，f1取最大值，即：

-g≤f1≤0

，

(8)

由式(4)(5)可知：当μf=0时，f2取最小值；当f1=-g时，μf=μr=1、m1和m3取最大值时，f2取最大值，即：

(9)

式中：m1+、m3+分别为m1、m3的最大值，m1-、m3-分别为m1、m3的最小值。

由式(6)知：当f1=0、μr=1、m2=m2+时，f3取最大值；若m2-≤m3+，则f3可取负值也可取零。即：

(10)

式中：m2-、m2+分别为m2的最小值、最大值。

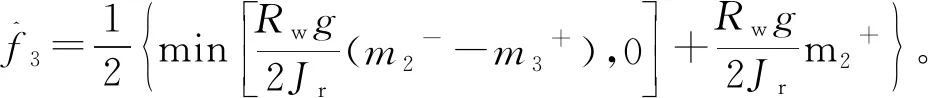
为得到最佳的控制制动力矩，式(8) ～(10)中的f1、f2和f3用其近似值来表示，结合式(7)可以得到较为精确的等效控制制动力矩

(11)

为了保证滑模面的收敛性，需满足关系式

(12)

式中k1、k2为常数。

ABS滑模变结构控制器输出控制前后轮的制动力矩

(13)

式中k3、k4为常数。

由式(11)～(13)可以得前后轮控制力矩

(14)

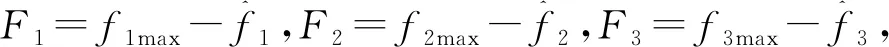
F1=0.5g，

由于滑膜控制的前后轮控制力矩中存在不连续函数sign，制动控制过程中易发生抖动，本文采用积分法消除抖动。定义积分滑模控制的前后轮滑移率跟踪误差

(15)

式中α1、α2为常数。

基于式(15)，重复上述求解滑模变结构控制器输出的前后轮制动力矩计算过程，用稳态函数sat(S)取代不连续函数sign(S)，由式(14)得到ABS控制器输出的前后轮制动力矩

(16)

式中φ1、φ2为常数。

3 EBD模糊控制器设计

EBD系统可以通过调节后轮轮缸压力，使后轮滑移率跟踪前轮滑移率，保证前后车轮能够同时抱死[22-24]。其模糊控制器的设计主要包括：模糊化、模糊推理和反模糊化。模糊控制采用双输入单输出二维模糊控制系统，2个输入变量分别为前后轮滑移率的差值e和前后轮滑移率差值的变化率ec，输出为后轮目标轮缸压力增量u。

模糊控制器输入和输出变量的模糊子集均为{NB，NM，NS，ZO，PS，PM，PB}，其中PB、PM、PS分别表示正大、正中和正小；NB、NM、NS分别表示负大、负中和负小；ZO表示零。e、ec、u的论域分别为[-0.1,0.1]、[-0.8,0.8]、[-1,1]。输入和输出变量的隶属度函数均采用三角隶属函数，如图2～4所示。

图2e的隶属函数 图3 ec的隶属函数 图4 u的隶属函数

e、ec分别有7个隶属函数，模糊控制规则有49条，采用 if A and B, then C的Mamdani模糊推理系统，表2为模糊控制器的模糊规则。

由表2可知：

ifeis NB， andecis NB， thenuis NB，

ifeis NS， andecis ZO，thenuis NS，

……

ifeis PB， andecis PM， thenuis PB。

表2 模糊控制规则

本文的模糊推理通过MATLAB的模糊逻辑工具箱实现，采用Mamdani最小推理法。反模糊化的方法有许多，本文采用重心反模糊法。

4 ABS/EBD系统仿真

为了验证本文建立的ABS、EBD控制器的控制效果，利用MATLAB/Simulink软件进行ABS滑模控制器与EBD模糊控制器的仿真试验验证。

4.1 ABS仿真

利用表1中参数在Simulink软件中建立车辆1/2模型，设定汽车在开始制动时的初始车速为30 m/s，假定在轮胎滑移率λ=0.2时取得最大地面纵向制动力，整个制动过程中汽车沿直线前进。

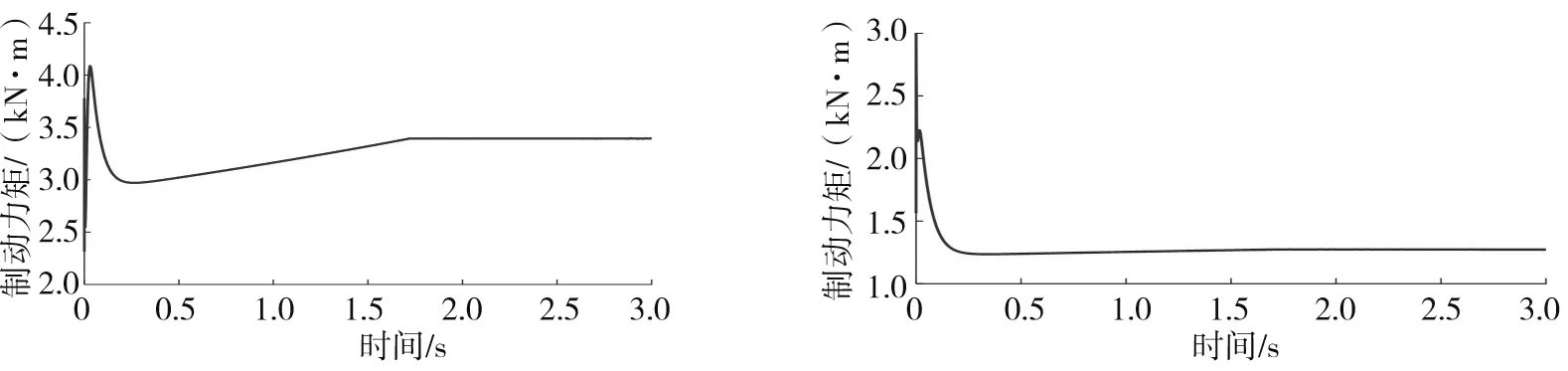
汽车以30 m/s的初速度在干沥青路面上进行直线制动时，仿真结果如图5、6所示。其中图5为制动过程中前、后轮滑移率与理想滑移率误差的变化曲线，图6为制动过程中前、后轮制动力矩的变化曲线。

a)前轮 b)后轮

a)前轮 b)后轮

由图5、6可以看出：ABS滑模控制器能够控制前后轮实际滑移率跟踪理想滑移率曲线的变化，控制误差在±0.010以内。制动时质心前移，前轮实际制动力矩大于后轮制动力矩，能防止后轮先于前轮抱死。

为进一步验证滑模变结构控制的效果，使汽车在不同的路面上进行制动仿真。汽车制动初始速度为30 m/s，第一秒行驶在湿沥青路面、第二秒行驶在雪路面。图7为前后轮滑移率与理想滑移率误差的变化曲线；图8为制动过程中前后轮制动力矩的变化曲线。

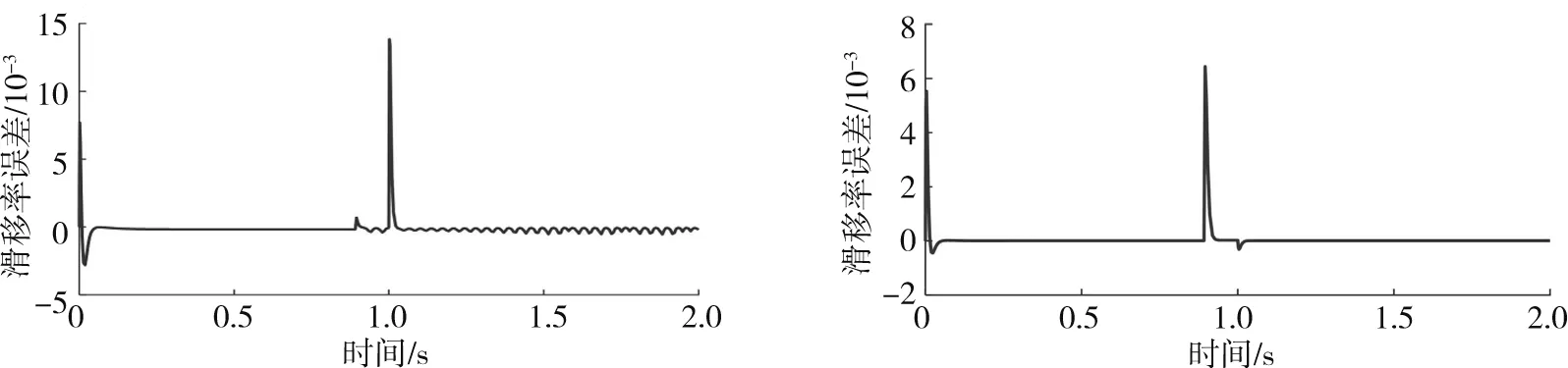
a)前轮 b)后轮

a)前轮 b)后轮

由图7、8可以看出：汽车在湿、雪路面上制动时，ABS滑模控制器能够控制前后轮滑移率跟踪理想滑移率，控制前轮滑移率误差在±0.015以内，后轮滑移率误差在±0.010以内。前轮实际制动力矩大于后轮，能够防止后轮先于前轮抱死拖滑。

4.2 EBD系统仿真

为验证本文建立的EBD控制器的有效性，假定汽车制动时初始车速为30 m/s，在干、湿沥青路面上汽车前轮轮缸压力以6 MPa/s递增，前后轮制动器制动力分配曲线如图9所示。

a)干沥青路面 b)湿沥青路面

由图9可以看出:EBD控制器可以动态调整前后轮制动器制动力的分配，使实际制动力分配曲线跟踪理想制动力分配曲线，保证制动初期充分利用地面制动力。

4.3 ABS/EBD系统仿真

汽车制动初始速度为30 m/s，假定制动开始汽车即进入EBD控制，当前后车轮滑移率达0.2时，ABS开始控制汽车的制动过程直至停车，分别进行干、湿沥青路面的制动仿真。图10为干、湿沥青路面上汽车制动过程中前后轮的滑移率曲线，图11为干、湿沥青路面上汽车制动过程中的制动力矩曲线。

a)干沥青路面 b)湿沥青路面

a)干沥青路面 b)湿沥青路面

由图10、11可以看出：制动初期前后轮滑移率达0.2之前，EBD系统介入控制，前后轮制动力矩按照理想制动力矩分配曲线变化，后轮滑移率跟踪前轮滑移率变化；当滑移率达到0.2时，EBD系统退出，ABS系统介入控制，前后轮滑移率保持最佳滑移率，防止前后车轮抱死拖滑，提高制动效率；整个制动过程中前轮制动力矩始终大于后轮制动力矩，防止后轮先于前轮抱死拖滑的危险工况发生。

5 结论

1)ABS滑模变结构控制器能够将车辆制动时前后车轮的滑移率维持在理想滑移率附近，采用积分滑模控制能很好地解决滑模变结构控制中的抖动问题。

2)EBD模糊控制器可以随时调整前后轮制动器制动力的分配，使前后轮制动器制动力曲线接近于理想制动器制动力曲线，保证车辆制动时的稳定性。

3)ABS/EBD系统在干、湿沥青路面上制动的联合仿真表明，整个制动过程中车辆的稳定性好，验证了本文设计的ABS/EBD系统控制器的有效性。