时延遥操作系统的非对称双通道波变量补偿法

戴沛， 黄攀峰，*， 鹿振宇， 刘正雄

1.西北工业大学 航天学院智能机器人研究中心， 西安 710072 2.西北工业大学 航天飞行动力学重点实验室， 西安 710072

时延遥操作系统的非对称双通道波变量补偿法

戴沛1,2， 黄攀峰1,2，*， 鹿振宇1,2， 刘正雄1,2

1.西北工业大学 航天学院智能机器人研究中心， 西安 710072 2.西北工业大学 航天飞行动力学重点实验室， 西安 710072

为保证遥操作系统在时延条件下的稳定性，以及减少传统波变量方法的跟踪误差，提出一种非对称双通道波变量补偿法。该方法在前向通道波变量补偿法的基础上，采用能量整定器对反向通道的波变量进行补偿。通过调节波阻抗、滤波器和能量整定器的相关参数可以充分保证遥操作系统的稳定性和跟踪性能。实验结果表明该方法在保证时延遥操作系统稳定性的基础上，速度跟踪平均误差比传统波变量法减少70%以上，力跟踪平均误差比前向通道波变量补偿法减少60%以上。为了比较不同时延下本方法的效果，设计时延分别为3 s和0.6 s的2种实验。结果表明本方法在不同时延条件下均可以取得较好的效果。

时延； 遥操作； 波变量； 跟踪性能； 稳定性

当前空间探索的需求增多，延长航天器使用寿命，降低维修成本成为各国航天领域研究和工程人员的共识。目前空间安装、维修任务仍旧主要依赖于航天员，这不仅花销巨大，而且威胁到航天员的生命安全[1-3]。采用人在回路的遥操作技术一方面可以降低空间维护成本，另一方面可以弥补空间机器人在轨操作智能程度不足的缺点。在操作过程中，遥操作给操作者提供了出色的临场感，使操作者不用置身于危险环境中进行操作。但遥操作系统的稳定性容易受到信道中时延的影响[4-5]，尤其是天地大回路遥操作，其时延区间一般在250 ms～3 s，普通的控制方法难以保证系统的稳定性。为了保证遥操作系统在变时延条件下的稳定性和性能，李智军等提出自适应模糊控制的方法及智能网络遥操作控制方法[6-9]。针对多个机器人协同遥操作和不定时延的情况，文献[7]中给出自适应模糊控制的方法，并结合马尔可夫过程对随机网络时延进行建模，最后设计一种自适应模糊控制方法。而对于定时延遥操作，Niemeyer和Slotine提出波变量的方法[10]，从而保证遥操作系统在定时延条件下的稳定性。该方法具有在任意定时延下保证系统无源性和稳定性的能力。但是该方法也具有跟踪误差大和存在波反射这两大问题。针对波反射问题，Niemeyer和Slotine提出阻抗匹配的方法[11]，将从端的控制器等效为与波阻抗相关的阻尼项。该方法消除了波反射，但并不能解决跟踪误差大的问题。Bate等采用去除反向通道波变量从端速度信息的方法[12]，与阻抗匹配方法相比减小了跟踪误差。

针对跟踪误差大的问题，Ye和Liu利用操作者感受到的力和从端控制力对前向通道波变量进行补偿的方法[13]，减小从端的轨迹跟踪误差。Li和Kawashima利用信道中传输的信息对前向和反向的波变量进行补偿的方法[14]，减小从端的轨迹跟踪误差并提高力反馈的逼真度。张永林和宋爱国分析了广义波变量遥操作系统的透明性[15]，给出最小波反射准则和严格阻抗匹配准则。崔艳和居鹤华给出基于波变量的时延双边遥操作系统设计方法[16]，在外部主从端之间直接引入PD调整器，提高从端的跟踪性，但力跟踪误差依然存在。

空间遥操作系统的稳定性和透明性是相互对立的2种性能，相对于波变量方法而言，可以保证遥操作系统在时延条件下具备较强的稳定性，但相应的跟踪性能会受到影响。波变量补偿法分为前向通道补偿和双向波变量补偿法，前向通道波变量补偿法利用速度或力等信息对前向传输的波变量进行补偿，从而消除误差项，提高轨迹跟踪能力。而双向波变量补偿法多为对称结构[14]，前向和反向波变量补偿量均采用能量整定器，会不可避免的牺牲部分操作性能来保证无源性。

针对上述问题，本文提出一种非对称双通道波变量补偿法。该法在前向通道补偿位置误差信息的基础上，通过反向通道对力误差信息进行补偿。由于前向通道和反向通道为非对称信息，需要通过分析其无源性得到参数取值范围。该方法在保证系统无源性的基础上，确保从端的实际速度跟踪主端的速度，并且使得从端的控制力真实的反馈到主端。

1 波变量的基本框架

1.1 波变量的基本定义

(1)

图1 通信信道的波变换
Fig.1 Wave transformation in communication channel

1.2 波变量与无源性

Niemeyer的研究表明将前向波变量信道中加入滤波器可以提高系统的无源性[17]。

(2)

则称该系统是无源的[18]。

波变量为二端口网络，其系统的供给率为

(3)

考虑信道时延的影响

(4)

则在能量域中，系统t时刻的存储能量为

(5)

式中：Estore(0)为系统初始时刻存储的能量；Estore(t)为系统在t时刻存储的能量；Pdiss为系统的耗散功率[19]。

将式(1)和式(4)代入式(5)，可得

(6)

式中：

1.3 基于波变量的遥操作

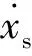
图2 基于波变量的遥操作
Fig.2 Wave variable based teleoperation

在频域中，式(1)变换为

(7)

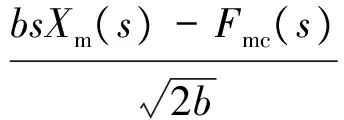
(8)

(9)

(10)

图2系统中的信道时延模型为

Vm(s)=Vs(s)e-sT

(11)

(12)

Xsc(s)和Xm(s)的关系为

(13)

从端反馈给主端的力为

Fmc(s)=Fsc(s)e-sT+bsXm(s)-sXsc(s)e-sT

(14)

Xsc(s)和Xs(s)的关系为

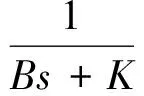
(15)

将式(15)代入式(13)，从端的实际位置为

(16)

理想情况下，从端能够跟踪主端的轨迹且主端能准确感受到从端的反馈力。故图2所示框架中的从端的实际位置Xs(s)和从端反馈给主端力Fmc(s)的理想目标分别为

(17)

Fmc(s)=Fsc(s)e-sT

(18)

相比于式(18)，式(14)中的b(sXm(s)-sXsc(s)e-sT)为力跟踪误差项。

2 非对称双通道波变量补偿法

非对称双通道波变量补偿法在前向通道波变量补偿法的基础上对反向通道波变量进行补偿，从而提高力跟踪性能。

本文将三螺旋理论引入到中高职衔接贯通培养机制研究中，可以更好地认识中高职院校与企业、政府之间的关系，更全面地实现中高职教育的人才培养目标， 更有效地推动中高职教育的校企合作发展。

2.1 前向通道波变量位置补偿

胡凌燕等[20]提出一种具有更好轨迹跟踪性能的前向通道波变量补偿法。该方法利用vs和fsc对前向通道波变量进行补偿。从而使从端的实际位置跟踪主端的位置。

该方法给出的前向通道波变量的补偿量为

(19)

控制框图如图3所示。

易得，补偿后的从端实际位置为

(20)

从而达到式(17)中从端位置的理想目标。但是，该方法并未对力跟踪性能进行改进，式(14)中的误差项依然存在。通过设计反向通道波变量补偿，保证整个系统的无源性的前提下力跟踪误差趋于0。不同于文献[20]，本文将虚线范围内的补偿项等效转化为实线的反馈补偿，从而便于在反向通道对力跟踪误差进行补偿。

图3 改进型前向通道波变量补偿法
Fig.3 Modified forward channel wave variable compensation method

2.2 反向通道波变量力补偿

在2.1节前向通道波变量补偿法的基础上，在反向通道波变量加入一个补偿项ΔVm(s)，反向通道波变量可以表述为

Vm(s)=Vs(s)e-sT+ΔVm(s)

(21)

因此，从端反馈给主端的力为

(22)

将式(21)和式(10)代入式(22)，则Fmc(s)为

Fmc(s)=Fsc(s)e-sT+

(23)

如果式(24)成立：

(24)

式(23)中的bsXm(s)-Xsc(s)e-sT项被抵消，符合式(18)的理想目标。

利用式(7)～式(10)，化简可得

(25)

将式(21)代入式(25)可得

ΔVm(s)=Um(s)-Us(s)e-sT

(26)

2.3 能量整定器

由于反向通道补偿项不可避免的将能量注入遥操作系统，可能会引起系统的不稳定[14]。故使用能量整定器来保证无源性。

根据文献[21]，定义一个能量池如式(27)，用于表示能量整定器所耗散的能量。

(27)

式中：Er(0)为能量池的初始值。

定义一个待补偿量，将输入能量整定器的变量与输出能量整定器的变量之差进行积分。

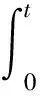
(28)

式中：

Δvm(τ)=um(τ)-us(τ-T)

(29)

最终，能量整定器的输出量vm(t)为

(30)

综上所述，本文所提出方法的整体框图如图4 所示。

图4 系统总体控制框图
Fig.4 Block diagram of overall system control scheme

3 无源性分析与参数设定

3.1 整个系统的无源性分析

整个遥操作系统由操作者、主端、信道、从端和环境等多个部分组成。主从端的操作机构采用质点模型。操作者和主端都具备无源性。所以控制方法设计时需要保证信道、从端和环境这3个部分的无源性。

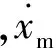
单端口网络的输入功率流为

(31)

则系统t时刻的储存能量为

(32)

如果式(32)成立，就可以保证单端口网络的无源性。从而保证整个遥操作系统的无源性。

若Estore(0)=0，式(32)等效为

图5 遥操作系统的各部分组成
Fig.5 Different regions in teleoperation system

(33)

3.2 基于无源性的系统参数设计

根据文献[23]，若波变量传递函数的幅值小于1就可以保证系统的无源性。调节参数使得|Vs(s)/Um(s)|≤1，即可保证区域②具备无源性。

根据Tanner的研究结果[24]，可得

(34)

|Gse(s)|s=jω=|V(s)/U(s)|≤1

(35)

根据文献[20],Vs(s)/Um(s)可以表述为

(36)

由式(36)可得，|Vs(s)/Um(s)|是λ和ω的函数。通过调节控制器参数并画出不同ω和λ时|Vs(s)/Um(s)|的曲线，就可以找出符合|Vs(s)/Um(s)|≤1的λ值。

令B=3.2 N·s/m，b=3.2，K=80 N/m，ms=0.5 kg，T=0.6 s，Genv=Ze=5 N·s/m，画出不同ω和λ值时的曲线(其中：ω作为横坐标，|Vs(s)/Um(s)|作为纵坐标，λ由1增加到20)。具体如图6 所示。

由图6(a)可知，当ω>30后，|Vs(s)/Um(s)|的值随ω的增大逐渐降低。图6(b)中的虚线表示λ=13时的情况，此时|Vs(s)/Um(s)|在ω=18取得峰值1.024。且图6表明，纵坐标的值随λ的增加而增加，所以当λ>13时的|Vs(s)/Um(s)|在峰值处均超过1。所以，选择λ=13，就可以保证前向通道和从端的无源性。

图6 |V(s)/U(s)|的幅值曲线
Fig.6 Magnitude curves of |V(s)/U(s)|

4 实验校验

4.1 实验建立

实验平台由一台惠普Z820工作站和一个Novint Falcon 手控器组成，详见图7。实验过程中，操作者操作Falcon手控器发出位置控制信号，再由MATLAB/Simulink的HAPTIK[25]工具箱读取主端的位置信息，通过虚拟定时延网络传递给从端。系统从端包含一个质点模型，从端通过与环境交互作用，将反馈力信息和位置信息反馈给主端，并通过HAPTIK工具箱给手控器设置反馈力，整个控制回路按照图4进行设计。操作过程持续时间为50 s，操作者只在手控器坐标系中的x方向进行操作，其他方向的速度和力均为0。图8为Simulink控制框图，各参数如表1 所示。由于波变量方法的特性，所以文本所设计的实验均是基于定时延情况。

图7 实验平台
Fig.7 Experiment setup

图8 Simulink的控制框图
Fig.8 Control loop in Simulink

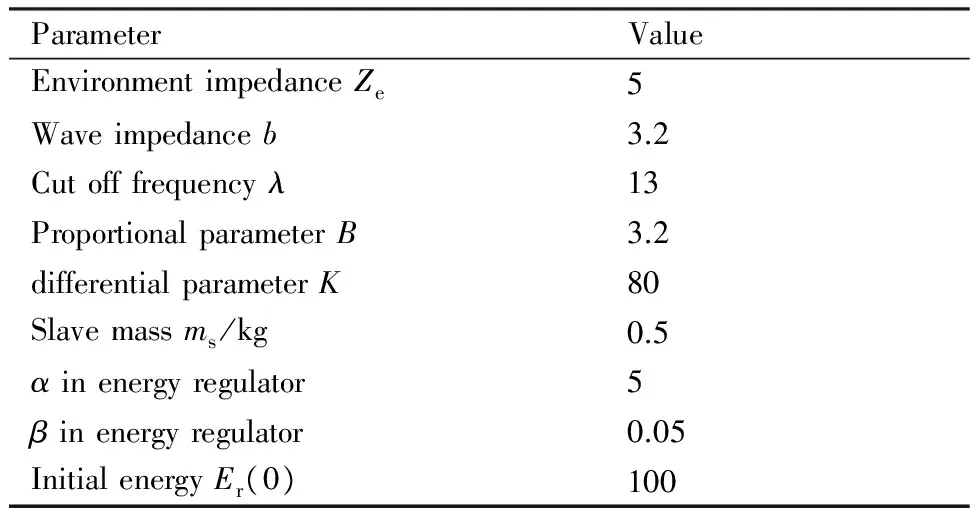
ParameterValueEnvironmentimpedanceZe5Waveimpedanceb3．2Cutofffrequencyλ13ProportionalparameterB3．2differentialparameterK80Slavemassms/kg0．5αinenergyregulator5βinenergyregulator0．05InitialenergyEr(0)100

4.2 实验结果

为比较本文方法在不同时延下的效果，本文设计2种时延条件，一种时延T=0.6 s，另一种时延T=3 s，每种时延下做3组实验，各组所采用的参数相同。实验1采用传统的波变量方法，实验2采用前向通道波变量补偿法，实验3采用本文提出的非对称双通道波变量补偿法。 图9和

图9 f(t)和f(t-T)曲线(T=0.6 s)
Fig.9 f(t) and f(t-T) curves with T=0.6 s

图10为T=0.6 s下曲线平移后的力跟踪和速度跟踪图。图11和图12为T=3 s下曲线平移后的力跟踪和速度跟踪图。

图和曲线(T=0.6 s)Fig.10 (t-T) and (t) curves with T=0.6 s

图11 f(t)和f(t-T)曲线(T=3 s)
Fig.11 f(t) and f(t-T) curves with T=3 s

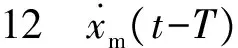
图和曲线(T=3 s)Fig.12 (t-T) and (t) curves with T=3 s

图9和图11表明，在力跟踪性方面，非对称双通道波变量补偿法比传统波变量法和前向通道波变量补偿法都具有很好的跟踪效果，实验3中的fmc(t)和fsc(t-T)的曲线重合度最高，实验1与实验2的曲线误差是由于式(14)中的b(sXm(s)-sXsc(s)e-sT)误差项未被抵消。图9(c) 中fsc(t-T)曲线在峰值时，fmc(t)与其有跟踪误差，其原因是反向通道能量整定器会影响主端力跟踪的响应速度。

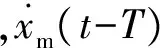
为了便于定量评估跟踪性能，速度跟踪和力跟踪平均绝对误差为

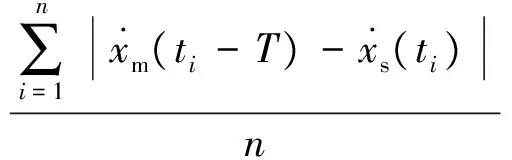
(37)

(38)

式中：n为数据点总数;Δverr为速度跟踪平均绝对误差;Δferr为力跟踪平均绝对误差。

当T=0.6 s时，从表 2 可以看出，在速度跟踪误差方面，非对称双通道波变量补偿法和前向通道波变量补偿法效果均较好，误差分别为0.011 8 m/s 和0.012 1 m/s，相比于传统的波变量方法的误差0.042 5 m/s分别减少了72%和71%。在力跟踪误差方面，非对称双通道波变量补偿法的误差仅为0.144 6 N，相比于传统波变量方法的和前向通道波变量补偿法分别减少了65%和66%。

当T=3 s时，非对称双通道波变量补偿法的速度跟踪误差为0.011 0 m/s，比传统波变量方法的0.053 4 m/s减少79%。力跟踪误差为0.098 2 N，比传统波变量方法的和前向通道波变量补偿法分别减少了76%和70%。实验结果表明本文算法在不同时延条件下均可以取得较好的效果。

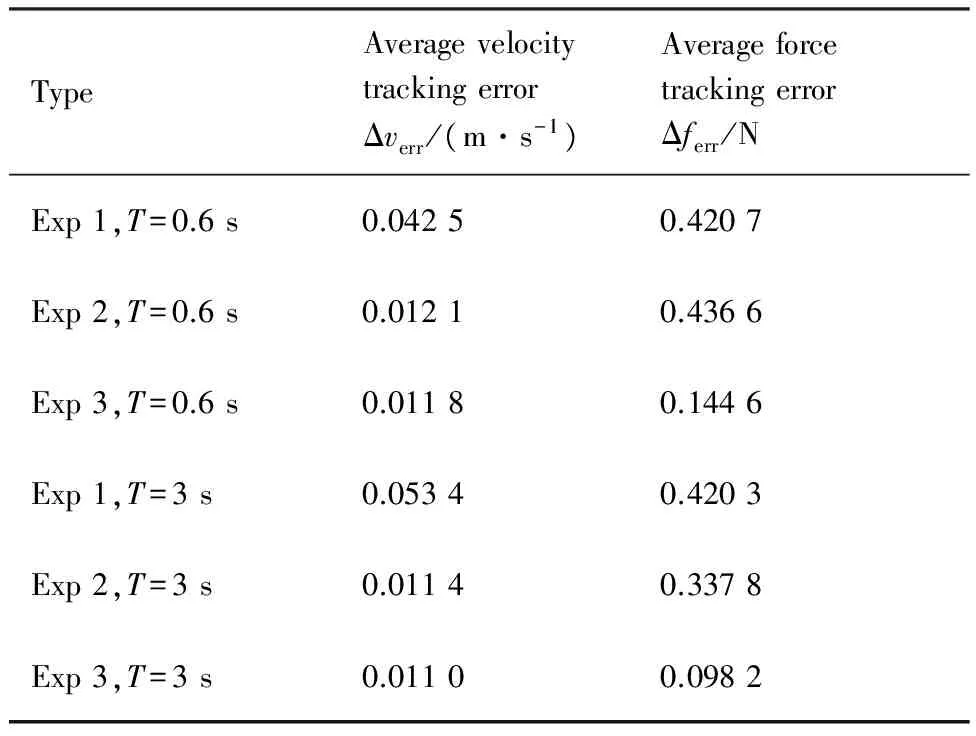
表2 不同实验的跟踪误差Table 2 Tracking errors in different experiments

为保证系统的无源性，记录单端口网络的能量(E2)，如图13所示。曲线表明，2种时延下的3组实验的能量均大于0，可以保证系统的无源性，具体证明见式(32)。

上述分析表明，本文所提的非对称双通道波变量补偿法具有较好的效果。但是本文的方法只局限于定时延遥操作系统。

图13 单端口网络的能量(E)
Fig.13 Energy in 1-port network (E)

5 结 论

波变量方法可以保证遥操作系统在任意定时延下的稳定性，但跟踪性能会受到大幅影响。仅通过前向通道波变量补偿可以在一定程度上保证遥操作系统的速度跟踪性，但力跟踪误差仍然存在。本方法在此基础上，提出非对称双通道波变量补偿法，前向通道对系统的位置速度跟踪误差进行补偿，反向通道对力跟踪误差进行补偿，同时利用能量整定器保证整个系统的无源性。实验结果表明，通过合理的参数设计，在不同时延下，本算法相比于传统波变量法速度跟踪误差减小70%以上，力跟踪相对误差比前向通道波变量补偿法减少60%以上。

[1] 张斌, 黄攀峰, 刘正雄, 等. 基于虚拟夹具的交互式空间机器人遥操作实验[J]. 宇航学报, 2011, 32(2): 446-450.

ZHANG B, HUANG P F, LIU Z X, et al. An interactive space robot teleoperation experiment based on virtual fixtures[J]. Journal of Astronautics, 2011, 32(2): 446-450 (in Chinese).

[2] 丁炳源, 黄攀峰, 刘正雄, 等. 速度型虚拟夹具辅助空间遥操作技术研究[J]. 航空学报, 2012, 34(6): 1436-1444.

DING B Y, HUANG P F, LIU Z X, et al. Research on space teleoperation technology assisted with velocity-based virtual fixture[J]. Acta Aeronautica et Astronautica Sinica, 2012, 34(6): 1436-1444 (in Chinese).

[3] 田志宇, 黄攀峰, 刘正雄. 辅助空间遥操作的虚拟管道设计与实现[J]. 宇航学报, 2014, 35(7): 834-842.

TIAN Z Y, HUANG P F, LIU Z X. Design and implementation of virtual tube as an aid for space teleoperation[J]. Journal of Astronautics, 2014, 35(7): 834-842 (in Chinese).

[4] OBOE R, FIORINI P. A design and control environment for internet-based telerobotics[J]. The International Journal of Robotics Research, 1998, 17(4): 433-449.

[5] 王永, 谢圆, 周建亮. 空间机器人大时延遥操作技术研究综述[J]. 宇航学报, 2010, 31(2): 299-306.

WANG Y, XIE Y, ZHOU J L. A researsh survey on teleoperation of space robot through time delay[J]. Journal of Astronautics, 2010, 31(2): 299-306 (in Chinese).

[6] LI Z J, XIA Y Q, SU C Y. Intelligent networked teleoperation control[M]. Berlin: Springer, 2015: 182-190.

[7] LI Z J, XIA Y Q, SUN F C. Adaptive fuzzy control of multilateral cooperative teleoperation for multiple robotic manipulators under random time delays[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(2): 437-450.

[8] LI Z J, CAO X Q, YANG Y, et al. Bilateral teleoperation of holonomic constrained robotic system with time-varying delays[J]. IEEE Transactions on Instrument & Measurement, 2013, 62(4): 752-765.

[9] LI Z J, CAO X Q, DING N. Adaptive fuzzy control for synchronization of nonlinear teleoperators with stochastic time-varying communication delays[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(4): 745-757.

[10] NIEMEYER G, SLOTINE J J E. Telemanipulation with time delays[J]. The International Journal of Robotics Research, 2004, 23(9): 873-890.

[11] NIEMEYER G, SLOTINE J J E. Stable adaptive teleoperation[J]. IEEE Journal of Oceanic Engineering, 1991, 16(1): 152-162.

[12] BATE L, COOK C D, LI Z. Reducing wave-based teleoperator reflections for unknown environments[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 392-397.

[13] YE Y, LIU P X. Improving trajectory tracking in wave-variable-based teleoperation[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(2): 321-326.

[14] LI H, KAWASHIMA K. Achieving stable tracking in wave-variable-based teleoperation[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(5): 1574-1582.

[15] 张永林, 宋爱国. 广义波变量遥操作系统的透明性分析[J]. 宇航学报, 2008, 29(2): 688-693.

ZHANG Y L, SONG A G. Analysis of transparency in generalized wave based teleoperation[J]. Journal of Astronautics, 2008, 29(2): 688-693 (in Chinese).

[16] 崔艳, 居鹤华. 基于波变量的时延双边遥操作系统设计[J]. 计算机测量与控制, 2012, 20(5): 1324-1325.

CUI Y, JU H H. Design of time-delayed bilateral teleoperation system based on adjusted wave variables[J]. Computer Measurement & Control, 2012, 20(5): 1324-1325 (in Chinese).

[17] NIEMEYER G. Using wave variables in time delayed force reflecting teleoperation[D]. Cambridge: Massachusetts Institute of Technology, 1996: 162-167.

[18] 王久和. 无源控制理论及其应用[M]. 北京: 电子工业出版社, 2010: 14-15.

WANG J H. Passivity-based control theory and its applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 14-15 (in Chinese).

[19] SLOTINE J J E, LI W. Applied nonlinear control[M]. Englewood Cliffs, NJ: Prentice-Hall, 1991.

[20] HU L Y, LIU X P, LIU G P. The wave-variable teleoperator with improved trajectory tracking[C]//2010 8th IEEE International Conference on Control and Automation (ICCA). Piscataway, NJ: IEEE Press, 2010: 322-327.

[21] CHING H, BOOK W J. Internet-based bilateral teleoperation based on wave variable with adaptive predictor and direct drift control[J]. Journal of Dynamic Systems, Measurement and Control, 2006, 128(1): 86-93.

[22] RAJU G J, VERGHESE G C, SHERIDAN T B. Design issues in 2-port network models of bilateral remote manipulation[C]//Proceedings of the 1989 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 1989: 1316-1321.

[23] TANNER N A, NIEMEYER G. Practical limitations of wave variable controllers in teleoperation[C]// Proceedings of the 2004 IEEE Conference on Robotics, Automation and Mechatronics. Piscataway, NJ: IEEE Press, 2004, 1: 25-30.

[24] TANNER N A, NIEMEYER G. Improving perception in time-delayed telerobotics[J]. The International Journal of Robotics Research, 2005, 24(8): 631-644.

[25] DE PASCALE M, DE PASCALE G, PRATTICHIZZO D, et al. The Haptik Library, a component based architecture for haptic devices access[C]//Proceedings of EuroHaptics, 2004: 365-370.

(责任编辑： 苏磊)

URL：www.cnki.net/kcms/detail/11.1929.V.20160530.1450.004.html

Asymmetrictwochannelwavevariablecompensationmethodforteleoperationsystemwithtimedelay

DAIPei1,2,HUANGPanfeng1,2,*,LUZhenyu1,2,LIUZhengxiong1,2

1.ResearchCenterforIntelligentRobotics,SchoolofAstronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.NationalKeyLaboratoryofAerospaceFlightDynamics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Inordertoguaranteesystemstabilityintimedelayedteleoperationandreducetrackingerrorsoftraditionalwavevariablemethod,theasymmetrictwochannelwavevariablecompensationmethodisproposed.Thismethodcompensatesthewavevariableinbackwardcommunicationchannelbyenergyregulatorbasedontheforwardwavevariablecompensationmethod.Bytuningtheparametersofwaveimpedance,andthecutofffrequencyofwavefilterandenergyregulator,thestabilityandtrackingperformanceofteleoperationsystemcanbeguaranteed.Byexperiments,itisrevealedthatthismethodreducesover70%averagevelocitytrackingerrorscomparedwiththetraditionalwavevariablemethodandreducesover60%averageforcetrackingerrorscomparedwiththeforwardwavevariablecompensationmethodintheconditionofensuringsystemstability.Forcomparisonofperformanceindifferenttimedelays,wedesigntwotypesofexperimentswithtimedelayof3sand0.6s.Theresultsrevealthatthismethodhasgoodperformanceintheconditionsofdifferenttimedelays.

timedelay;teleoperation;wavevariable;trackingperformance;stability

2016-03-16；Revised2016-05-18；Accepted2016-05-23；Publishedonline2016-05-301450

s：NationalNaturalScienceFoundationofChina(11272256,61005062,60805034)

.E-mailpfhuang@nwpu.edu.cn

2016-03-16；退修日期2016-05-18；录用日期2016-05-23； < class="emphasis_bold">网络出版时间

时间：2016-05-301450

www.cnki.net/kcms/detail/11.1929.V.20160530.1450.004.html

国家自然科学基金 (11272256,61005062,60805034)

.E-mailpfhuang@nwpu.edu.cn

戴沛， 黄攀峰， 鹿振宇， 等． 时延遥操作系统的非对称双通道波变量补偿法J． 航空学报,2017,38(2):320225.DAIP,HUANGPF,LUZY,etal.AsymmetrictwochannelwavevariablecompensationmethodforteleoperationsystemwithtimedelayJ.ActaAeronauticaetAstronauticaSinica,2017,38(2):320225.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0158

V557+.5; TP242.3

A

1000-6893(2017)02-320225-11