模式稳定层次高 外表朴实内涵深*——2017年江苏省数学高考试题评析与教学启示

●

(大厂高级中学,江苏 南京 210044)

模式稳定层次高外表朴实内涵深*
——2017年江苏省数学高考试题评析与教学启示

●余建国

(大厂高级中学,江苏 南京 210044)

2017 年江苏省数学高考试题延续往年的“江苏模式”，稳中有变，整卷难度均衡，考查全面，设计新颖． 试题很好地体现了数学计算、抽象概括、直观想象、推理论证、数学建模、数据分析等核心素养，较好地实现了区分功能，对高中数学教学具有良好的导向作用．

数学高考; 江苏卷; 试题评析; 教学启示

2017年的江苏卷在《普通高中数学课程标准(实验)》的框架内，从考试内容、形式和文理区分等方面，坚持特色鲜明的“江苏模式”，很好地贯彻了《考试说明(江苏卷)》的“保持相对稳定，命题稳中有新；坚持以人为本，确保社会稳定”和“科学性、规范性、公平性、稳定性、选拔性、导向性”的命题要求，延续了数学高考江苏卷的一贯风格．笔者结合自己的高三教学实践，对此谈一些粗浅的认识，请批评指正．

1 特点分析

1．1 延续模式，稳中有变

文献[1]介绍了“江苏模式”，2017年试题延续了江苏卷自主命题的一贯风格，即卷Ⅰ共6个解答题：第15，16题是三角函数与向量、立体几何平行和垂直证明；第17，18题是应用题、圆锥曲线；第19，20题分别是函数与导数、数列综合．稍微变化的是：1)立体几何证明题10年来第一次与三角和向量解答题交换顺序，变为第一道解答题，事实上这两道题都比较简单，是否需要交换顺序无关紧要；2)应用题以立体几何为背景考查求大小，而不是最常见、考生最习惯的求最值类问题(下文详述)，避免了基本不等式或导数的反复考查；3)在卷Ⅱ第22，23题(这两道题理科考生必做)中，一改空间向量与概率分布“轮流坐庄”的模式，第22题考查空间向量、异面直线所成角和二面角等基础知识，考查运用空间向量解决问题的能力，第23题将计数原理、排列组合与二项式定理、离散型变量的概率分布结合起来考查，这样理科的两个重点内容首次在同一张试卷中都考到，对教学起到了良好的导向作用．

1.2 回归教材，不偏不怪

2017年的江苏卷总体难度稳定．卷Ⅰ满分160，其中填空题平均分为51.88，解答题平均分为44.84，省平均分为96.72，难度系数0.605；卷Ⅱ满分40，省平均分为23.67,与前几年基本相当．

基本题均改编或来源于教材，能迅速消除考生的紧张情绪，有利于考生较快拿到基本分，为其较好地进入答题状态作好铺垫．例如，填空题前10题，考查最基本的概念，运算简单，有的心算便可完成；解答题前两道题涉及的是一些常用方法，与教材上相关章节的练习题型类似、难度相当．

例1某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总储存费用为4x万元．要使一年的总运费与总储存费用之和最小，则x的值是______．

(2017年江苏省数学高考试题第10题)

分析本题直接来源于课本，也是学生耳熟能详的题目，经过适当改编，主要考查学生应用基本不等式求最值和数学建模能力(此为C级考点)．笔者认为，应用基本不等式求最值虽说是“必考点”，但对繁、难的配凑技巧要有度的把握．有的模拟试卷过分强调配凑技巧，是片面理解教学要求．

中等题主要考查考生对数学概念和性质的了解情况以及基本运算能力，如填空题的倒数第3题和第4题以及解答题的中间两道题，虽有一定的运算量，但所用的方法都是课本上最常见的，中等及以上程度的考生应能顺利作答．

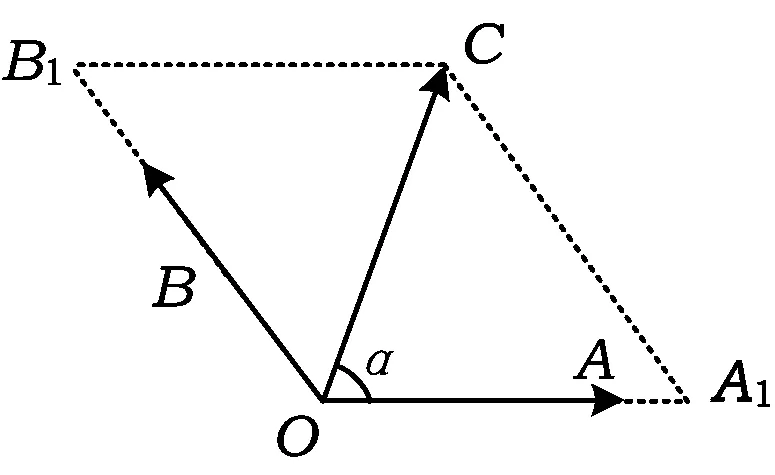
图1

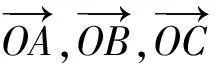
( 2017年江苏省数学高考试题第12 题)

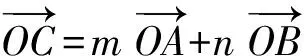
分析如图1，以OC为对角线，构造以OA1，OB1为邻边的OA1CB1．在△OA1C中，∠OCA1=∠COB1=,由tanα=7，得

由正弦定理，得

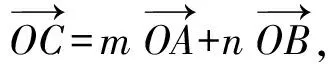
所以

m+n=3.

1.3 应用变脸，核心算理

数学模型是数学与现实世界、其他学科联系的桥梁．数学建模的教学有利于学生感悟数学与现实世界的联系，养成从整体的角度看待和思考的习惯，积累运用数学语言表达现实问题、运用数学知识解决实际问题的经验，从而提升数学应用意识和创新能力．数学建模是数学核心素养之一，江苏卷基本都在第17，18题的位置安排应用题．与以往都是“建立目标函数求最值”型不同的是，2017年应用题以立体几何为背景“求长度”．

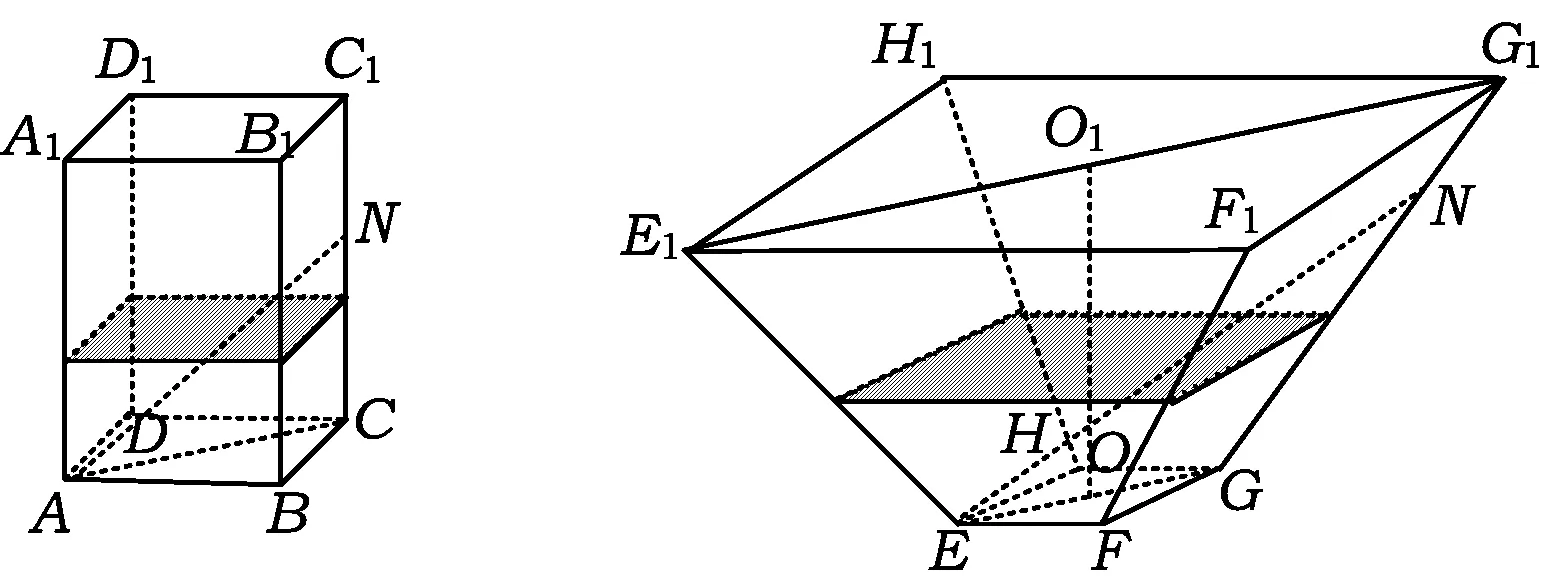
图2 图3

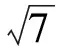
1)将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中的长度；

2) 将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中的长度．

( 2017年江苏省数学高考试题第18 题)

分析对于第2)小题，大部分学生想到解三角形(详见参考答案)，或建立坐标系．笔者用解析法试做后发现：求点N(玻璃棒l与棱GG1的交点)的坐标(x，y)时，要解方程

25x2-16×28x+16×142-1 600×9=0，

即便算出Δ=1 327 104，开方也是个难题．如何改进解析法呢？

以E为坐标原点、EG所在直线为x轴建立如图4所示的直角坐标系，则G(14，0)，G1(38，32)．设玻璃棒l与水面的交点为M，则EM为所求.易知EN=40，可设N(40cosα，40sinα)，因为点G，N，G1共线，所以

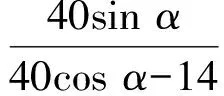
又(30sinα-40cosα)2+(30cosα+40sinα)2=502，

(2)

将式(1)代入式(2)，得

(30cosα+40sinα)2=482，

从而 30cosα+40sinα=48,

(3)

联立式(1)和式(3)，得

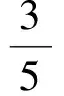
故

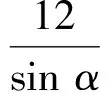
由此可见，简化运算的核心是式(2)．数学运算是数学核心素养之首，运算准确是基本，算理正确是核心．在高强度的考试氛围中，选择合理的运算路径基本靠“感觉”，一般很难做到好中选优．笔者在QQ群中有幸见到南京师范大学单墫老先生“晒的墨宝”，寥寥几行，轻松挥就，不愧为数学解题专家．

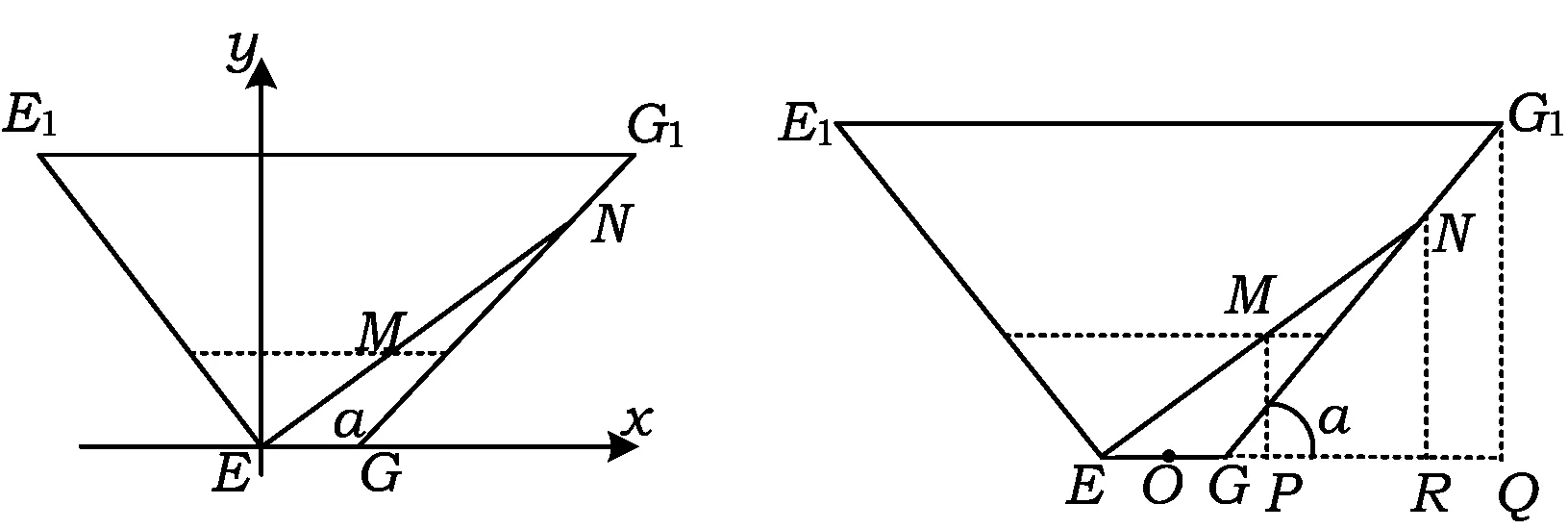
图4 图5

如图5，四边形E1EGG1是等腰梯形，过点G1作高G1Q⊥EG于点Q，则

G1Q=32=8×4.

又作NR⊥EQ,垂足为R,则

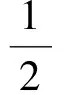
在Rt△GG1Q中，

GG1=8×5=40(勾三股四弦五).

因为G1Q∥NR，在Rt△GNR中，可设NR=4x，GR=3x,在Rt△ENR中，

EN2=ER2+NR2，

即

402=(14+3x)2+(4x)2，

所以

4x=24(x=6)， 14+3x=32 ．

过点M作MP⊥EQ，垂足为P，则MP=12，再由相似可得

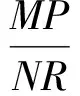
1.4 函数零点，耳目一新

高中代数知识与方法涉及集合、逻辑知识、函数、数列、解析几何、概率统计等众多分支，但就代数的历史发展而言，方程与函数应成为高中代数的核心．因此要仔细研究方程与函数中的思想与方法，使之成为代数推理的“工具包”．例如，填空题第14题以方程解的个数为背景，通过转化、化归为函数问题，渗透数形结合的思想，既有直观形象，又有精细刻画；推理方法既包含直接推理，也包含间接推理，对学生的代数推理能力提出了较高的要求．

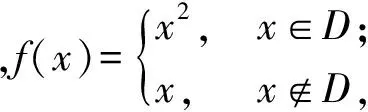
(2017年江苏省数学高考试题第14 题)

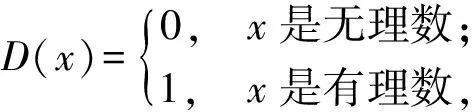
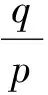
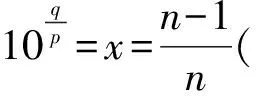
此式左边是10的整数次幂，右边是非整数，这是矛盾的．而此时(x-k)2为有理数，从而lgx=(x-k)2无解．也就是说，交点属于每个周期x∉D的部分，且在x=1处，

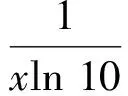
因此在x=1附近仅有一个交点．

本题作为填空压轴题，集中体现了数学抽象、逻辑推理、直观想象等核心素养，是难得一见的好题．因此，高三复习教学不能盲目地做题，也不能在无多大数学意义的变式上浪费时间，复习的真谛应是进一步理解数学的本质，螺旋上升，发展学生的数学思维能力．

1.5 多题把关，思维严谨

把关题题目设计亲切，每个小题由易到难，层层推进，既能使不同层次的考生拿到分，又较好地体现了高考的选拔功能．如解答题的最后两道题，考查的是最简单的等差数列和三次函数，第1)小题考生应该感到很容易上手，后面的小题设计比较新颖，虽有一定的思维量，但涉及的都是中学数学中基本的知识点和方法，如有时间仔细思考，应该都能找到解题的思路和方法，会发现其方法都是平时知道的，无需特别的技巧和方法．

例5已知函数f(x)=x3+ax2+bx+1(其中a>0，b∈R)有极值，且导函数f′(x)的极值点是f(x)的零点(极值点是指函数取得极值时对应的自变量的值)．

1)求b关于a的函数关系式，并写出定义域；

2)证明：b2>3a；

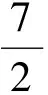
(2017年江苏省数学高考试题第20 题)

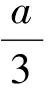
对于第2)小题，由第1)小题可知

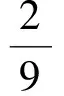
要证b2>3a，只要证

在定义域a∈(3，+∞)的前提下，这个“双三次”不等式不难证明.

对于第3)小题，理解题设不难，难在代数式的变形．

第19题数列综合题、第20题函数与导数题集中反映了严谨思维、推理论证的要求．代数推理既包括演绎推理，也包括合情推理，因此特殊化和一般化也成为代数推理的一项基本技能，这在第19题中体现得淋漓尽致.因篇幅所限，本文不再赘述．

2 教学启示

纵观2017年江苏省数学高考卷，延续了2008年以来的模式，知识点分布、考查要求与近几年的江苏卷基本一致.我们从中发现规律，服务教学，提高高三数学复习效率，在减轻学生学习负担的同时，也减轻教师自己的负担，在发展学生的数学思维和核心素养上多下功夫．

2.1 培养运算能力

运算求解是核心素养之首，也是数学考试的必备技能．准确是运算的最基本要求，但只有清晰、合理的算理才能产生效益．解题训练中需注重算理的培养，包括理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果．平时指导学生注意运算与推理的结合，利用算理简化运算过程或寻找更为合理的运算程序，教师绝不能越俎代庖，思路代替不了运算．

2．2 夯实“四基三会”

从“双基”到“四基”是提高学生素质、发展学生能力的需要，史宁中先生积极倡导的“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”(即“三会”)更是高度概括了学生数学思维发展的方向．教材是学生学习基础知识、形成基本技能的“蓝本”，是数学思想方法的载体，是开展数学基本活动的剧本．教材的例习题都具有一定的典型性，无论是平时教学，还是总复习，都要紧扣《考试说明》，吃透教材，用好教材，充分发挥教材的基础与示范作用[3]．

2.3 培养核心素养

正如前文所分析，试题全面体现了数学运算、抽象概括、逻辑推理、直观想象、数学建模、数据分析等核心素养．高考题具有导向性，在即将全面推开的新的课程改革中，数学教学需要站在更新、更高的角度，把发展学生的数学核心素养作为数学教育的终极目标，在平时的教学中，教师应有针对性地对学生进行训练、培养和发展．

[1] 余建国．提升模式层次 创新模式内涵——2016 年江苏省数学高考试题评析[J]．中学教研(数学)，2016(10)：32-24．

[2] 刘定定．三次函数的图像与性质[J]．中学生数学，2012(2)：7-8．

[3] 董荣森．“四基三能”并重 凸显数学核心素养——2016年高考数学江苏卷评析与启示[J]．数学通讯，2016(8)：1-5．

2017-08-01

余建国(1965-)，男，江苏南京人，江苏省特级教师.研究方向：高中数学解题与课堂教学．

O12

A

1003 - 6407(2017)11-35-04