中心自同构几乎是内自同构的有限p-群

张博儒,郭秀云

中心自同构几乎是内自同构的有限p-群

张博儒,郭秀云

(上海大学理学院,上海200444)

有限p-群G的中心核K(G)是G的每一中心自同构都不变的全体元素所构成的子群.如果G是幂零类为2的p-群,首先给出了|Autc(G):Inn(G)|与|Z(G):K(G)|相等的充分必要条件，其次研究了|Autc(G):Inn(G)|与|Z(G):K(G)|相差一个p的倍数的条件.

中心自同构;中心核;内自同构

本工作中所讨论的群都是有限群,且p恒表示素数.

群G的一个自同构α称为G的一个中心自同构.如果α与G的每一内自同构可交换或等价,则对于G的任意元素x都有x−1xα∈Z(G).显然,群G的所有中心自同构构成G的自同构群Aut(G)的一个正规子群,记为Autc(G).因而一个自然的问题是:什么样的群能满足Autc(G)=Aut(G)?实际上,这个问题已经被许多学者关注[1-4].进一步,Curran等[5]研究了满足条件Autc(G)=Inn(G)的p-群,并对于p-群G给出了Autc(G)=Inn(G)的充分必要条件.这里,p-群G的幂零类为2当且仅当Inn(G)≤Autc(G).本工作将在Inn(G)≤Autc(G)的前提下,研究指数|Autc(G):Inn(G)|和指数|Z(G):K(G)|的关系.实际上,对于p-群G,显然Inn(G)≤Autc(G)当且仅当K(G)≤Z(G),这里

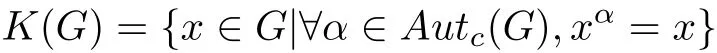
称为群G的中心核.注意到G′≤K(G),证明如下.

设G是幂零类为2的非交换p-群.|Autc(G):Inn(G)|=|Z(G):K(G)|当且仅当Z(G)是循环群.

进一步地，考虑|Autc(G):Inn(G)|/|Z(G):K(G)|=p的情形.

1 预备知识

如果一个非交换群G没有非平凡的交换的直因子,则称G为纯非交换群.显然,一个非交换p-群G的中心Z(G)循环,那么G一定是一个纯非交换p-群.用Hom(G,H)表示群G到交换群H的全体同态映射所成的群,用Cm表示阶为m的循环群,r(G)为群G的秩.如果G 是一个p-群,则 Ωi= 〈x ∈ G|xpi=1〉,

引理1[5]设G是幂零类为2的p-群.

(1)G′≤Z(G);

(2)exp(G′)=exp(G/Z(G));

(3)如果exp(G′)=pc，则存在交换群C 使得G/Z(G)～=Cpc×Cpc×C.

引理2 设G为纯非交换p-群.|Autc(G)|=|Hom(G/K(G),Z(G))|.

证明 根据文献[6]可知,对于纯非交换p-群G,|Autc(G)|=|Hom(G,Z(G))|,即对于任意的σ∈Autc(G)和任意的g∈G,都存在fσ(g)=g−1σ(g)使得fσ∈Hom(G,Z(G))与σHom(G/K(G),Z(G)),故|Autc(G)|=|Hom(G/K(G),Z(G))|.

引理3[5]设Cn,Cm和Cd分别是阶为n,m和d的循环群.如果d=gcd(m,n),则

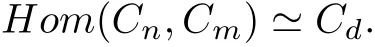
引理4[7]设A,B和C为交换群.

(1)Hom(A×B,C)⋍Hom(A,C)×Hom(B,C);

(2)Hom(A,B×C)⋍Hom(A,B)×Hom(A,C).

引理5[5]设A和B为交换p-群且C,D分别为A和B的子群(商群),则Hom(C,D)同构于Hom(A,B)的一个子群. 更进一步地,令 pm= min{|A|/|C|,|B|/|D|},则

引理6[5]设G=A×N,其中A为交换p-群且A/=1,N 为纯非交换p-群.如果Inn(G)≤ Autc(G),则 |Autc(G):Inn(G)|＞ p2.

引理7 设G是幂零类为2的纯非交换p-群且G/Z(G),G′,K(G),Z(G)的秩分别为t,d,s,z,则

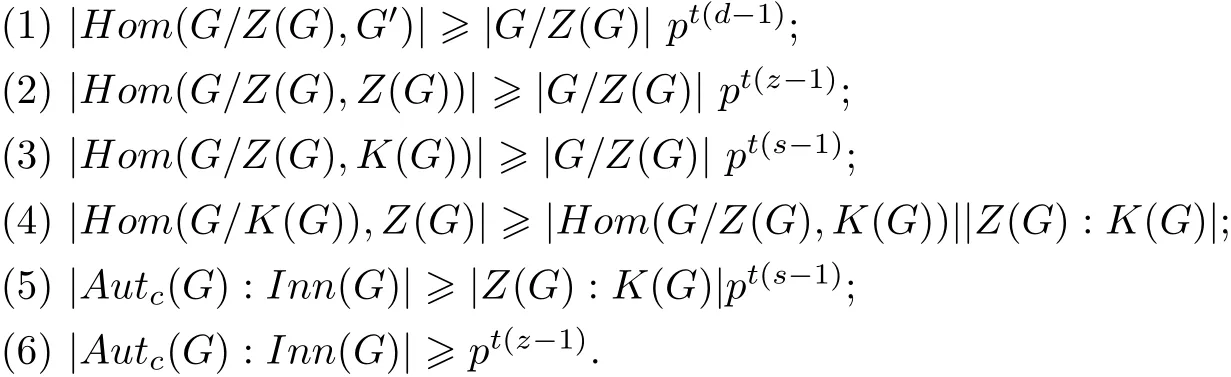
证明 引理7的(1),(2)可从文献[5]得到.由于exp(G/Z(G))=exp(G′)≤exp(K(G)),又由 r(K(G))=s,r(G/Z(G))=t,得 |Hom(G/Z(G),K(G))|≥ |G/Z(G)|pr(s−1).(4)可由引理5得.(5),(6)可由(2),(3),(4)得.

引理8[5]设A,B分别为交换p-群和循环p-群.如果exp(A)≤exp(B),则Hom(A,B)⋍A.

引理 9[5]设G是幂零类为2的p-群.如果Z(G)循环,则 |Autc(G):Inn(G)|=|Z(G):G′|.

引理10 设A,B分别是阶为pt和ps的循环群.

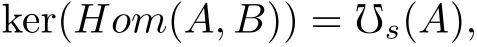
式中,

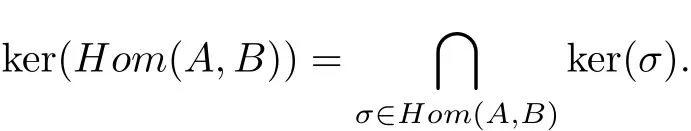
证明 为方便设A=〈a〉,B=〈b〉.如果t＞s,则存在A到B的同态映射进而ker(f)= 〈aps〉,故 ker(Hom(A,B))≤ 〈aps〉. 又对于任意 σ ∈ Hom(A,B),显然有 A/ker(σ)～=σ(A)≤ B,故 pt−s=|A|/|B|≤ |A|/|σ(A)|=|ker(σ)|. 又由于循环群 A 有唯一的 pt−s阶子群 〈aps〉,故 〈aps〉≤ ker(σ). 进而 〈aps〉≤ ker(Hom(A,B)),故 ker(Hom(A,B))= 〈aps〉. 如果t≤s,则存在A 到B 的同态映射易得ker(f)=1,故ker(Hom(A,B))=1.

引理11 如果A,B,C为交换群,则

(1)ker(Hom(A×B,C))≥ker(Hom(A,C))×ker(Hom(B,C));

(2)ker(Hom(A,B×C))=ker(Hom(A,B))∩ker(Hom(A,C)).

证明 (a)设g=(a,b)∈ker(Hom(A,C))×ker(Hom(B,C)).根据引理4中的(1),对于任意α ∈ Hom(A×B,C),都存在 α1∈ Hom(A,C),α2∈ Hom(B,C)使得(a,b)α=aα1bα2,故 gα=(a,b)α=aα1bα2=1.所以 (1)成立.

(b)设a∈ker(Hom(A,B))∩ker(Hom(A,C)).根据引理4中的(2),对于任意α∈Hom(A,B ×C),都存在 α1∈ Hom(A,B), α2∈ Hom(A,C),使得 aα=(aα1,aα2).因此aα=(aα1,aα2)=(1,1),从而 ker(Hom(A,B))∩ker(Hom(A,C))≤ ker(Hom(A,B ×C)).反之,对任意a∈ker(Hom(A,B×C)),根据引理4中的(2),对任意α1∈Hom(A,B),α2∈Hom(A,C),都存在 α ∈ Hom(A,B ×C)使得 (aα1,aα2)=aα.因此 (aα1,aα2)=aα=(1,1),从而ker(Hom(A,B×C))≤ker(Hom(A,B))∩ker(Hom(A,C)),ker(Hom(A,B×C))=ker(Hom(A,B))∩ker(Hom(A,C)).

由于

故由情形1,2知,|Autc(G):Inn(G)|/|Z(G):K(G)|≥p2.

证明 根据文献[10]可得.

引理15 设G是幂零类为2的纯非交换p-群,K(G)为pt阶循环群且r(Z(G))=z.|Autc(G):Inn(G)|/|Z(G):K(G)|≥ pz−1.

证明 由于cl(G)=2,故Inn(G)≤Autc(G),于是K(G)≤Z(G).可设Z(G)⋍Cpt+e1×Cpe2×···×Cpez.又由于G是纯非交换p-群,则根据引理2与4可知,

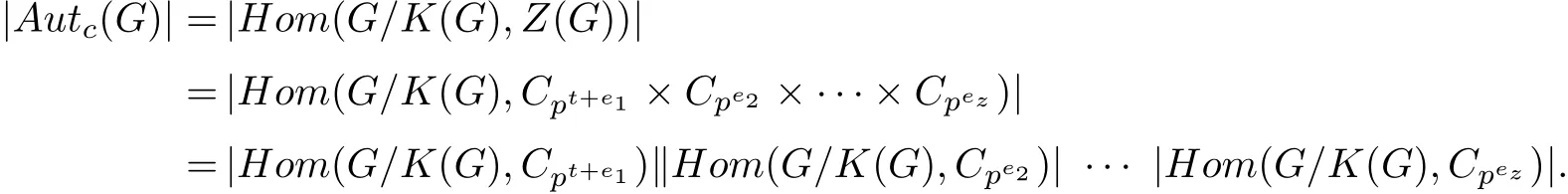
|Hom(G/K(G),Cpt+e1)|≥|Hom(G/S(G),Cpt+e1)|=|G/S(G)|=|G/Z(G)|pe1=pt+e1.又由于r(G/K(G))≥r(G/Z(G))≥2,则对于任意2≤i≤z,|Hom(G/K(G),Cpei)|≥pei+1.故 |Hom(G/K(G),Z(G))|≥ |G/Z(G)|pe1+e2+···+ez+z−1, 从而 |Autc(G):Inn(G)|/|Z(G):K(G)|≥ pz−1.

2 主要结果

定理1 设G是幂零类为2的非交换p-群,则|Autc(G):Inn(G)|=|Z(G):K(G)|当且仅当Z(G)是循环群.

证明 充分性.由于Z(G)循环,故G是纯非交换p-群.由于cl(G)=2,故Inn(G)≤Autc(G),进而 K(G)≤ Z(G),由引理 1得,exp(G/Z(G))=exp(G′)|Z(G)/K(G)|≤exp(K(G))|Z(G)/K(G)|=exp(Z(G)).于是由引理2与8可知,|Autc(G)|=|Hom(G/K(G):Z(G))|=|G/K(G)|,故|Autc(G):Inn(G)|=|Z(G):K(G)|.

必要性.令|Autc(G):Inn(G)|=|Z(G):K(G)|.根据引理13可知,G为纯非交换p-群.于是由引理7中的(5)可知,r(K(G))=1,即K(G)为循环群,故根据引理15可知,Z(G)是循环群.

推论1 设G是幂零类为2的非交换p-群.若Z(G)循环,则K(G)=G′.

证明 由引理9和定理1可知,|Z(G):K(G)|=|Z(G):G′|.又G′≤ K(G),故G′=K(G).

推论2 设G是非交换p-群.Autc(G)=Inn(G)当且仅当Z(G)=G′且Z(G)循环.

证明 充分性.由定理1充分性显然.

必要性.由于Autc(G)=Inn(G),根据引理6得,G是纯非交换p-群.又由引理7中的(6)知,Z(G)循环.由定理1和推论1可知,Z(G)=G′.

定理 2 设G是幂零类为2的非交换p-群,|Z(G):K(G)|=pe,则|Autc(G):Inn(G)|/|Z(G):K(G)|=p当且仅当G满足下列条件之一.

(1)K(G)=G′是阶为pc的循环群,Z(G)⋍Cpc+e−1×Cp,G/K(G)⋍Cpc+e×Cpc;

(2)K(G)=G′是阶为p的循环群,Z(G)⋍Cp1+e1×Cpe2,G/K(G)⋍Cp1+e×Cp(e1+e2=e,e2≥2).

证明 必要性.由于|Autc(G):Inn(G)|/|Z(G):K(G)|=p,故由引理13和引理7中的(5)知,G为纯非交换p-群且K(G)为循环群.不妨令K(G)⋍Cpt.根据引理15和定理1可知,r(Z(G))=2.又K(G)≤Z(G),故可设Z(G)⋍Cpt+e1×Cpe2.于是

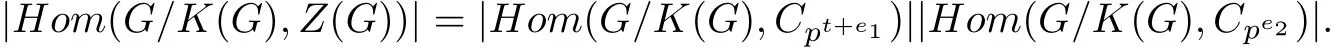
充分性.首先证G为纯非交换p-群.若否,则不妨设G=A×B,其中A为交换p-群且A/=1,B 为纯非交换 p-群.由于 K(G)=G′=B′,故 G/K(G)=G/G′=AB′/B′×B/B′.又因为r(B/B′)≥2且r(G/K(G))=2,所以AB′/B′=1.于是A=1,与假设矛盾,故G是纯非交换p-群.

再证|Autc(G):Inn(G)|/|Z(G):K(G)|=p.如果Z(G)⋍ Cpc+e−1×Cp,G/K(G)⋍Cpc+e×Cpc,则根据引理3和4可知,|Autc(G)|=|Hom(G/K(G),Z(G))|=|Hom(Cpc+e×Cpc,Z(G))|=p2c+e+1.又由于|Z(G):K(G)|=pe,|G/Z(G)|=p2c,则|Autc(G):Inn(G)|/|Z(G):K(G)|=p.如果Z(G)⋍Cp1+e1×Cpe2,G/K(G)⋍Cp1+e×Cp(e1+e2=e,e2≥2),则根据引理3和4可知,|Autc(G)|=|Hom(G/K(G),Z(G))|=|Hom(Cp1+e×Cp,Cp1+e1×Cpe2)|=pe+3.又由于|Z(G):K(G)|=pe,|G/Z(G)|=p2,故|Autc(G):Inn(G)|/|Z(G):K(G)|=p.

推论3 设G为非交换p-群.如果|Autc(G):Inn(G)|=p2,则群G具体如下.

(1)如果|Z(G):K(G)|=p2,则 Z(G)是循环群;

(2)如果|Z(G):K(G)|=p,则 Z(G)不循环,K(G)循环且G/K(G),Z(G)的秩为2;

(3)如果Z(G)=K(G),则K(G)不循环.

证明 由引理7、定理1和2易得.

[1]CURRAN M J.A non-Abelian automorphism group with all automorphisms central[J].Bull Austral Math Soc,1982,26:393-397.

[2]GLASbY S P.2-groups with every automorphism central[J].J Austral Math Soc Ser A,1986,41:233-236.

[3]MORIGI M.On the minimal number of generators of f i nite non-Abelian p-groups having an Abelian automorphism group[J].Comm Algebra,1995,23(6):2045-2065.

[4]赵立博,郭秀云.特定阶的子群都同构且交换的有限p-群[J].应用数学与计算数学学报,2013,27(4):517-521.

[5]CURRAN M J,MC CAUGHAN D J.Central automorphisms that are almost inner[J].Comm Algebra,2001,29(5):2081-2087.

[6]ADNEYJ E,YEN T.Automorphisms of a p-group[J].Illinois J Math,1965,9:137-143.

[7]SHARMA M,GUMbER D.On central automorphisms of f i nite p-groups[J].Communications in Algebra,2013,41:1117-1122.

[8]俞曙霞.有限交换p群的自同构群[J].广西大学学报(自然科学版),1983,25(2):90-95.

[9]BIDwELL J N S,CURRAN M J,MC CAUGHAN D J.Automorphisms of direct products of f i nite groups[J].Arch Math,2006,86:481-489.

[10]AN L J,DING J F,ZHANG Q H.Finite self dual groups[J].J Algebra,2011,341:35-44.

Finite p-groups with central automorphism almost being inner automorphism

ZHANG Boru,GUO Xiuyun
(College of Sciences,Shanghai University,Shanghai 200444,China)

Let G be a f i nite p-group and let K(G)be a subgroup of G consisting of all elements in G f i xed by every central automorphism in G.A necessary and sufficient condition is given on|Autc(G):Inn(G)|=|Z(G):K(G)|for a f i nite p-group G of class 2.The condition for|Autc(G):Inn(G)|=p|Z(G):K(G)|is also studied.

central automorphism;central kernel;inner automorphism

O 152.1

A

1007-2861(2017)05-0714-08

10.12066/j.issn.1007-2861.1744

2016-01-06

国家自然科学基金资助项目(11371237)

郭秀云(1956—),男,教授,博士生导师,研究方向为有限群论.E-mail:xyguo@staf f.shu.edu.cn