新疆喀什高台民居地基变形影响下缺陷协同演化分析
孟 丹, 庞 峰
新疆喀什高台民居地基变形影响下缺陷协同演化分析
孟 丹1, 庞 峰2
(1.青岛农业大学建筑工程学院,山东青岛266109;2.青岛理工大学艺术学院,山东青岛266033)
针对地基变形引起的新疆喀什高台民居砌体结构建筑物开裂损伤的工程实际情况,借助协同学的方法,选取序参量为建筑物裂纹在坐标系方向上投影矢量和的夹角,在考虑涨落的情况下利用势函数的特征,通过将平衡相变系统的熵类比到协同系统来研究其相变特征,以揭示建筑物受到地基变形影响过程中的相变行为及序参量的演化规律.分析结果表明,砌体结构建筑物裂纹演化的过程与建筑物的自由能紧密相关,根据建筑物自由能变化规律及其相关影响因素,可以获得建筑物的开裂损伤演化规律,进而为高台民居地基变形引起的建筑物损伤防护提供理论依据.
高台民居;地基变形;缺陷;协同演化
高台民居为高约40 m、长约800 m的黄土高崖上的维吾尔族聚居区,位于新疆维吾尔自治区喀什市老城东北端,是展示维吾尔族古代民居建筑和民俗风情的一大景观(见图1),距今已有600多年的历史.针对高台民居维护方面的研究,目前的成果更多的是从建筑景观和地质灾害的角度出发[1-5],以及从边坡稳定性的角度出发[6-7],而从建筑物地基变形引起建筑物开裂破坏方面的研究较少.然而,高台民居超过98%的建筑结构形式为土木、砖木以及砖混结构,该类结构形式对地基的变形十分敏感.因此,本工作以高台民居建筑物保护为目的,通过协同学的方法研究地基变形引起的建筑物开裂损伤演化问题,为更好地传承中国历史建筑文化遗产、保护高台民居区居民的生命财产安全提供理论参考.

图1 喀什高台民居Fig.1 High loess slopes in Kashgar
1 工程概况
本工作的研究对象为高台民居中的一栋砌体结构建筑物(见图2).可以看出,在地基变形的影响下,建筑物的墙体出现了裂缝.这主要是因为地基变形引起建筑物内部的附加应力不断增大,当附加应力值超过结构的强度极限时,就会导致建筑物的墙体和其他构件出现开裂损伤.

图2 地基变形影响下开裂的砖木Fig.2 Masonry structure inf l uenced by deformation of foundation
2 砌体构件裂纹演化的相变分析
2.1 序参量的选取
在地基负曲率变形影响下,建筑物内部的附加应力会导致墙体产生正八字裂缝和水平裂缝[8-10](见图3).建筑物左半部分(地基变形槽中心线为界)的正八字裂缝平行于坐标系x方向,右半部分的正八字裂缝平行于坐标系y方向.为了采用协同学的方法分析建筑物的损伤演化过程,选取序参量如下:建筑物左半部分所有裂缝在平行于裂纹开展方向和垂直于该方向的投影矢量的矢量和为L;右半部分所有裂缝在两个方向的投影矢量的矢量和为R.由于裂纹最初是随机分布的,那么初始的L和R的方向相同,都是坐标系第一象限夹角平分线的方向.如果取两个矢量和的夹角为序参量,并且为了方便计算分析,对该序参量用数学方式进行归一化处理——取两侧矢量和的夹角与π/2的比值代表序参量(用符号q表示),则初始时建筑物的裂纹是随机分布的,序参量q的值为0;随着地基变形的增大,建筑物裂纹从无序向有序发展,L顺时针旋转,R逆时针旋转,q由0逐渐增大,最终趋近于1.

图3 地基沉降影响下建筑物裂纹分布及序参量的变化Fig.3 Crack distributions and variations of order parameters in building under the inf l uence of foundation settlement
与上述情况相反,当地基变形为正曲率时序参量q同样由0逐渐增大,此时建筑物左右两侧的裂纹在坐标轴方向上投影的矢量和分别向相反方向旋转,建筑物出现倒八字裂缝.
2.2 砌体结构自由能表达形式
将建筑物看作一个系统,假设其自由能为F,根据协同学原理,如果附加应力作用下建筑物的名义应力为σ,则自由能可以表示为[11-13]

在临界点的邻域内,将F用q展开可得

对于地基变形影响下的建筑物,根据前面的描述可知序参量q具有反演对称性,因为序参量前面的正负号仅是同一应力状态下不同坐标系的结果,因此可以取

同时,由于在临界点邻域的q很小,可以忽略高次项的影响,即

式(4)也可以表示为
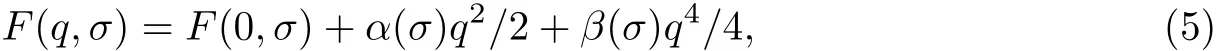
式中,α(σ)=F′′(0,σ)是外参量,随着地基变形引起建筑物内部附加应力的变化,建筑物的名义应力不断变化,对应的α(σ)可以从负值转变为正值,同时系统由一相转变到另一相,
根据协同学的原理可知,出现几率最大的相和自由能最小的相就是宏观上能实现的相.因此,通过自由能的极值条件

可计算出无序相和有序相的序参量的值为

式中,q01=0代表无序相,q02=±(−α/β)1/2代表有序相.
无序相:∂2F(q,σ)/∂q2= ∂2(F(0,σ)+α(σ)q2/2+β(σ)q4/4)/∂2q= α +3βq2> 0,将q01=0代入得出无序相的α>0;有序相:q02要有实根,而β>0,故要求α<0,因此在临界点处 ∂2F/∂q2=0,α =0.
2.3 相变分析
在相变过程中的临界点处α=0,无序相和有序相的自由能表达式分别为F(q01,σ)=F(0,σ)和F(q02,σ)=F(0,σ)−α2/(4β),即有序相和无序相的自由能相等,那么临界点处的自由能是连续的.
由自由能给出连续相变系统的序参量方程为

利用式(8),根据建筑物在附加应力作用下的名义应力可以确定建筑物的相变过程.
3 砌体构件裂纹演化考虑涨落的相变特征分析
考虑涨落的作用,在非平衡相变分析中系统的动力学方程表达为朗之万方程[12]

式中,F(t)为涨落力,且具有白噪声的性质,即

相应的Fokker-Plank方程(Fokker-Plank equation,FPE)为

式中,f=f(q,t)为t时刻序参量q的概率分布.对于自然边界条件,式(12)的定态解为
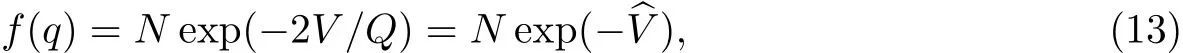

通过式(14)可以定性分析系统的宏观变化.势函数曲线随着外参量α值的变化如图4所示.可以看出,当α<0时,系统有3个定态,在q01=0处,势变为极大值,所对应的定态不稳定;势的极小值出现在q02=±(−α/β)1/2处,这两处对应的两个定态在宏观上均能实现,α=0为临界点.当α>0时,势函数的值均为非负,此时所对应的定态是宏观上能实现的态.

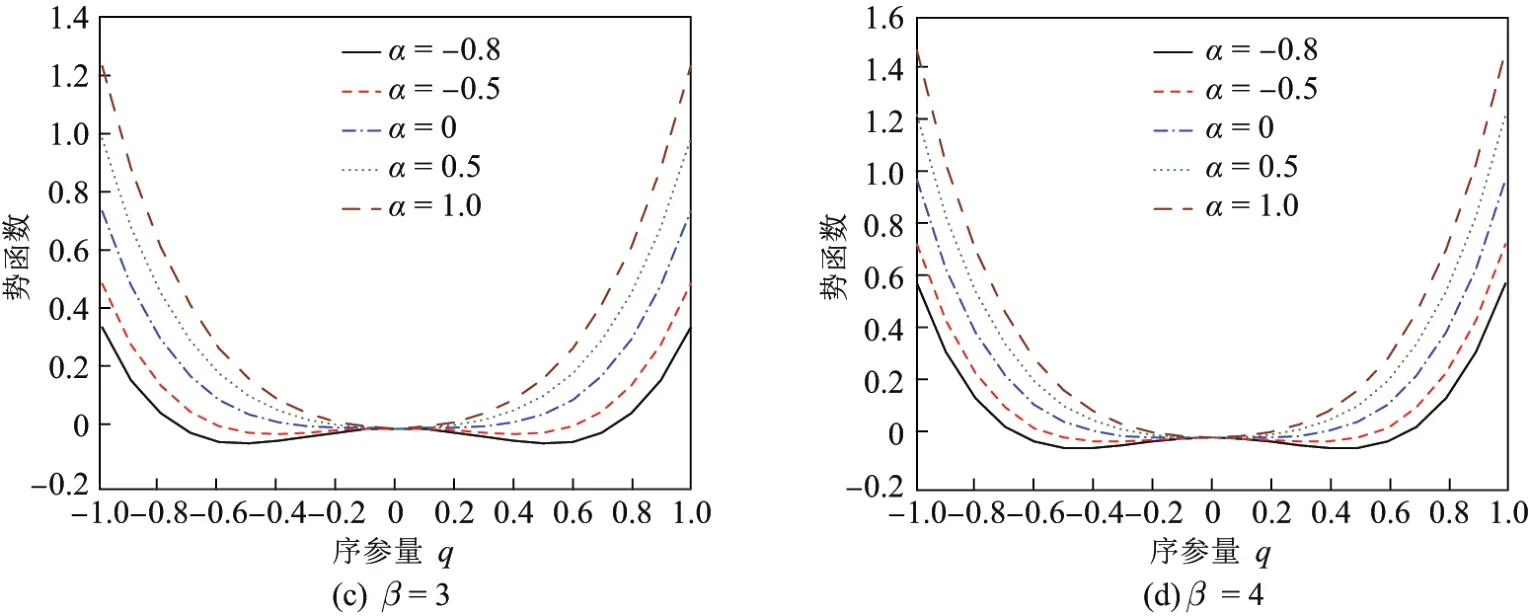
图4 不同α值对应的势函数曲线Fig.4 Potential function curves for dif f erent α values
图5描述了α取值不同时,β值和势函数曲线的关系.可以看出,势函数曲线随着β值的增大逐渐变得陡峭.并且,当α<0时,随着β值的增大,其稳定平衡点q02=±(−α/β)1/2的绝对值逐渐减小.

图5 不同β值对应的势函数曲线Fig.5 Potential function curves for dif f erent β values
用第2节所述方法可以求得系统无序相和有序相的序参量分别为q01=0和q02=±(−α/β)1/2,并且在临界点处α=0.
对于非平衡相变系统的熵,一般类比到协同系统的〈q2〉,通过推导得[12]

因此无序相和有序相两相的熵分别为 〈q2〉1= −1/α 和 〈q2〉2=(−α/β)/2−1/α,在临界点处α=0,可知熵是连续的.
无序相和有序相两相比热分别为 C1= ∂〈q2〉1/∂α =1/(2α2) 和 C2= ∂〈q2〉2/∂α =−1/(2β)+1/(2α2),在临界点处,C1−C2/=0,比热有一突变.
4 砌体结构裂纹演化过程的相变描述
上述过程在地基变形影响下的砌体结构建筑物裂纹演化中的相应描述如下:在建筑物尚未受到地表变形产生附加应力的作用时,α是一个非负值.随着附加应力逐渐增大,α值逐渐减小,但只要保证α>0,q=0就是系统的稳定平衡点,该平衡点在α=0时达到一种随遇平衡状态,此时的平衡点即为建筑物的相变点;随着α的继续减小,稳定平衡点变为不稳定平衡点,同时又出现两个新的稳定平衡点q02=±(−α/β)1/2,其中正号的平衡点对应于建筑物下方地表变形为负曲率变形,负号的平衡点对应于建筑物下方的正曲率变形.
5 结束语
本工作利用协同学原理,以受地基变形影响的建筑物两侧裂纹在坐标轴方向投影矢量和的夹角与π/2的比值为序参量,通过计算进行序参量演化分析和相变分析.研究结果表明,建筑物的自由能不仅决定序参量q演化方程中系数α和β的取值,还决定了q的相变点及其稳定性.因此,通过研究建筑物损伤过程中的自由能变化规律及其相关影响因素,可以获得建筑物的损伤演化规律,进而为高台民居地基变形引起的建筑物损伤防护提供理论依据.
[1]王小东,刘静,倪一丁.喀什高台民居的抗震改造与风貌保护[J].建筑学报,2010(3):78-81.
[2]蔡森.喀什高台民居建筑特色保护与更新的探索[D].乌鲁木齐:新疆师范大学,2010.
[3]王晨,庞峰.喀什高台民居地道安全隐患分析与治理对策优化[J].河南理工大学学报(自然科学版),2013,32(6):751-755.
[4]马小军,贺根义.新疆喀什市高台民居区崩塌地质灾害与治理研究[J].中国水运,2014,14(4):237-238;185.
[5]张玮.喀什市老城区高台民居边坡稳定性研究[D].青岛:青岛理工大学,2011.
[6]刘森林.中国传统民间住宅建筑研究[J].上海大学学报(社会科学版),2008,15(4):107-111.
[7]褚雪松,李亮,张玉强.新疆喀什高台民居边坡拐点附近三维楔形体的稳定性分析[J].石河子大学学报(自然科学版),2012,30(3):386-388.
[8]于广明,杨伦,苏仲杰,等.地层沉陷非线性原理、监测与控制[M].长春:吉林大学出版社,2000.
[9]时伉丽,丁虎,陈立群,等.移动载荷黏弹性Pasternak地基梁动力学响应[J].上海大学学报(自然科学版),2012,18(6):617-621.
[10]JADAAN O M,POwERS L M,GYENkENYESI J P.Multixial creep life prediction of ceramic structures using continuum damage mechanics and the f i nite element method[J].Journal of Engineering for Gas Turbines and Power,1999,121(4):577-585.
[11]KRAjCINOvIC D.Creep of structures—a continuous damage mechanics approach[J].Journal of Structural Mechanics,1983,11(1):1-11.
[12]潘永战.城市隧道施工引起建筑结构协同损伤理论及其应用[D].青岛:青岛理工大学,2012.
[13]RISkEN H.The Fokker-Plank equation:methods of solution and applications[M].Berlin:Springer,1984.
Synergetic evolution analysis of building defects under inf l uence of foundation deformation of high loess slopes in Kashgar,Xinjiang
MENG Dan1,PANG Feng2
(1.School of Architectural Engineering,Qingdao Agricultural University,Qingdao 266109,Shandong,China;2.Academy of Art,Qingdao Technological University,Qingdao 266033,Shandong,China)
To deal with the cracking damage caused by foundation deformation in masonry buildings of the high loess slopes in Kashgar,Xinjiang,the phase change behavior and evolution of order parameter in the loading of buildings are studied by comparing the entropy of the equilibrium phase transformation system to the cooperative system.Order parameter is represented by the angle between vector sums of the crack projected onto the coordinate system.The results show that evolution of the crack in masonry structure is closely related to the free energy of the building.Study on the variation of free energy in the process of building damage and its related factors can help understand the evolution of building damage,and provide a theoretical basis for preventing damage due to foundation deformation for high loess slopes in Kashgar.
high loess slope;deformation of foundation;defect;synergetic evolution
TU 362
A
1007-2861(2017)05-0772-08
10.12066/j.issn.1007-2861.1717
2015-11-26
新疆维吾尔自治区喀什市老城区高台民居保护改造研究资助项目(13YJA760036)
孟 丹(1980—),男,博士,研究方向为建筑物损伤检测、风险评价等.E-mail:md1101@163.com
本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

