时变系数自回归模型参数的贝叶斯估计
陈云仙,高星月,王钰莹,何幼桦
时变系数自回归模型参数的贝叶斯估计
陈云仙,高星月,王钰莹,何幼桦
(上海大学理学院,上海200444)
针对时变系数的自回归模型,假设其系数的先后状态具有一定相关性.在仅有一条样本函数的情况下,运用贝叶斯方法给出一阶模型参数估计的表达式.通过数值模拟展示了模型系数的取值和样本容量对估计效果的影响.实证分析表明,该估计方法所得的统计结果能够较好地揭示实际问题的内在规律性.
时变系数;自回归模型;贝叶斯估计;人均GDP
对于一般的时间序列,当观察时间较长时其内在结构可能会随时间发生变化,针对这类现象学者们提出了各种不同的时变模型.Dahlhuaus[1]对平稳时间序列进行拓展,丢弃平稳性的假设,给出了一般非平稳过程的通用估计方法——一般最小距离估计,即Whittle方法的一般化,并给出了估计的步骤,将得到的结果与最小二乘估计的结果进行比较,结果表明在异方差的情况下最小二乘估计不如最小距离估计有效.West等[2]提出了一种新的建立在非平稳时间序列模型上的分析方法,该方法将时间序列分解成一系列带有时变频率内容的部分;将这种分析方法应用于脑电图(electroencephalogram,EEG)时间序列分析,只要确定了这些潜在的部分,就可以得到脑电图时间序列在频率结构变化方面的定量比较.Prado等[3]针对不确定阶数的时变自回归(time-varying autoregressive,TVAR)模型进行了研究,该研究假设模型阶数的演化过程是在有界范围内离散的随机游走过程,其自回归系数采用贝叶斯方法估计.Bibi等[4]研究了模型系数根据已知的固定周期发生转换的一类时间序列,给出了参数估计强一致性和渐进正态性的条件,以及模型系数的估计量为伪广义最小二乘估计量的均值.Francq等[5]对时变滑动平均自回归(autoregressive moving average,ARMA)过程进行了研究,与以往不同的是,该模型系数的时变性体现在过程中的马尔可夫链机制重复出现非周期性变化;另外,还给出了最小二乘估计量和伪广义最小二乘估计量满足一致渐进正态性的具体条件.Triantafyllopoulos等[6]对带有时变系数的高斯滑动平均(moving average,MA)过程进行了估计与预测,认为模型系数噪声的方差是时变的,且方差呈指数形式随时间衰退;同时假设模型系数的演化是缓慢的,在默认时间序列是局部平稳的情况下,采用了贝叶斯方法进行研究.Nakajima等[7]也采用了贝叶斯方法,对时变系数的向量自回归(vector autoregression with time-varying parameter,TVP-VAR)模型进行了研究.该研究假设模型的系数和噪声方差的对数服从随机游走过程,并将该方法应用于日本的经济和货币政策进行了实证分析.Ijima等[8]给出了时变自回归过程系数明确的回归方法,即将模型系数看成事先确定的一组基函数的线性组合.王永民等[9]针对TVAR的时变系数建立一个向量自回归时间序列模型,利用最小二乘法计算系数矩阵,并给出了时变自回归序列点预测和区间预测的方法.Bekiros[10]研究的对象是TVP-VAR模型,其独特之处在于将TVP-VAR模型的表达式转换成一个多元状态空间的表达式.在状态空间系统下,有观察等式和状态等式两种状态,状态等式中的变量可能是可观察的,也可能是不可观察的,可以通过卡尔曼滤波来进行估计.Barnett等[11]对时变系数的时间序列进行了综合研究,其目的是对内在结构变化的英国GDP增长、通货膨胀和短期的利息率进行预测,为此将各种时变系数的模型进行了比较.
本工作所讨论的TVAR模型与上述模型不同的是,没有对模型参数施加服从随机游走过程之类的限制,而是仅假设不同时刻的参数之间存在一定相关性,且时间间隔越短其相关性越强.只要参数连续依赖于时间,那么这个假设的要求并不高.关于样本观察次数,在可以获得多条样本数据的情况下,用最大似然估计方法即可解决模型的参数估计问题.但由于时间的不可重复性,在很多情况下只能获得单条样本,那么最大似然估计方法将无法得到有效的估计,故本工作采用贝叶斯方法来解决单条样本下模型的参数估计问题.
1 模型及参数估计方法
对于时间序列{xt},满足时变系数自回归模型
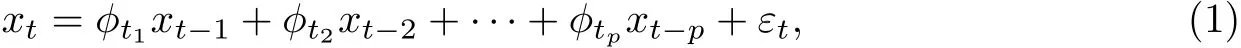
对于TVAR模型,p阶与一阶模型的推导原理类似.为了简洁起见,仅对TVAR(1)模型进行讨论,最后将给出p阶情形的描述.TVAR(1)模型为

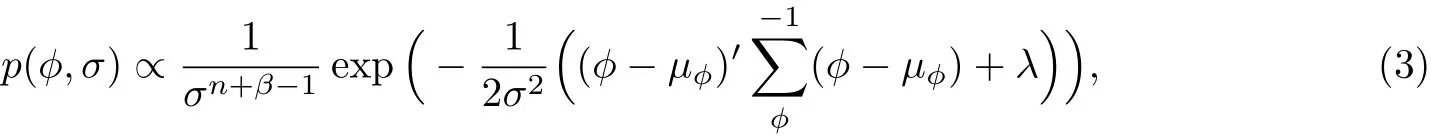

式中,
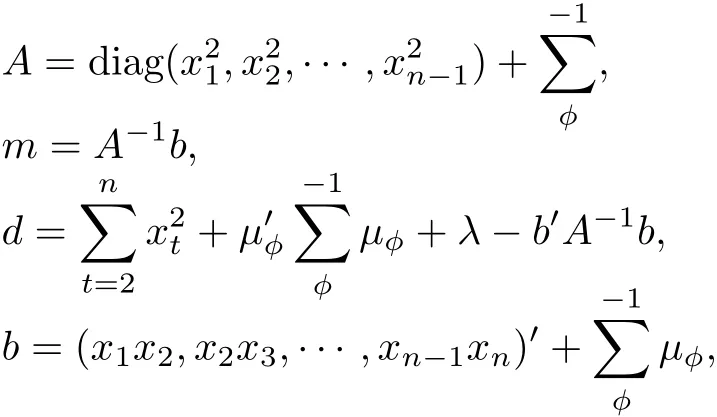
则

对于n+β>2以及|A|>0,
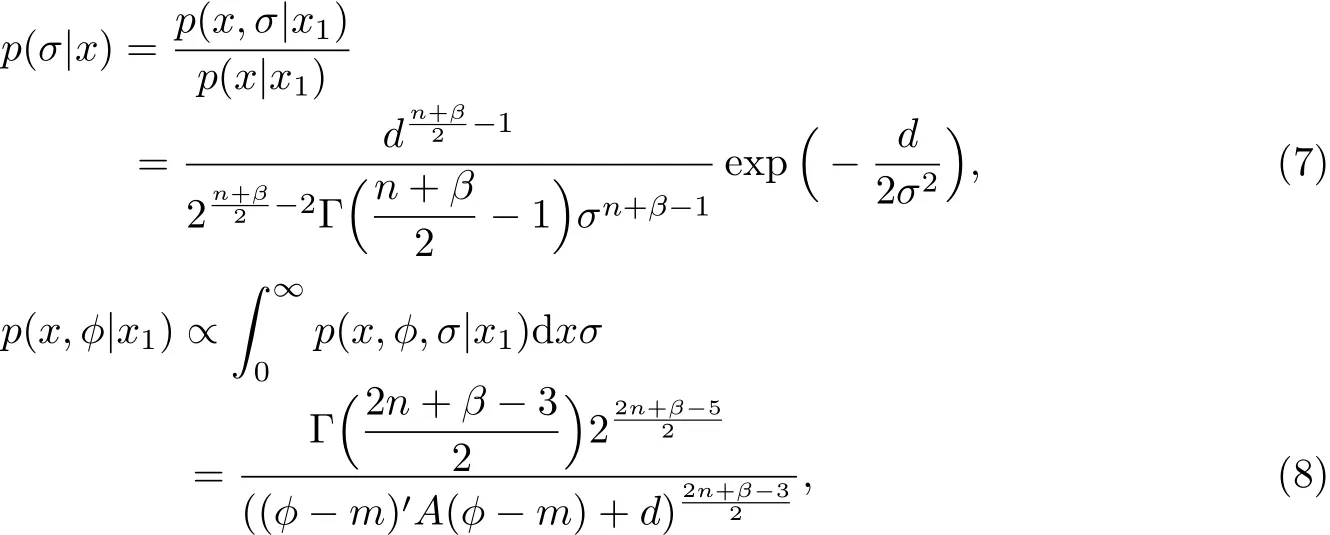

在二次损失下,n+β>3时,φ的贝叶斯估计为

σ的贝叶斯估计为

2 数值模拟
本工作采用随机模拟方法对所得估计量的性能进行研究.重复生成已知内在规律的时间序列样本数据来研究估计量(10)和(11)的统计特性.

式中,r为相邻时刻φt之间的相关系数.
2.1 两个时变模型估计的直观效果
第一个时变模型取φ(t)=sin(2πt).T=2,n=200,{εn}iid~N(0,1).假设φ的先验均值为µφ=0.就一次模拟样本得到参数估计为b σ(t)=0.945 5(σ的真实值为1).参数φ的估计值和真实值如图1所示.

图1 φ(t)及其贝叶斯估计值bφ(t)(模型1)Fig.1 φ(t)and its Bayesian estimationbφ(t)(model 1)
假如对参数φt的变化趋势有一定了解,那么在先验分布中令µφ=0.5φ,在这组模拟样本下得 σb=0.972 3,的分量均方误差值降至0.029 6.

图2 φ(t)及其贝叶斯估计值bφ(t)(模型2)Fig.2 φ(t)and its Bayesian estimationbφ(t)(model 2)
2.2 估计量的均方误差及收敛性计算
本工作通过重复的数值模拟,研究了不同样本长度对估计精度的影响.模拟时选定φ(t)=sin(t2+t),离散化后的随机扰动项仍为{εn}i~idN(0,1).记N次随机模拟中t时刻参数的第k次估计值为则衡量参数φ的均方误差(mean square error,MSE)和全局均方误差(global mean square error,GMSE)分别定义为

衡量参数σ的均方误差值为

本工作分别模拟了样本长度为50,150,300和400的样本,作为小样本、中等样本和大样本的代表.图3中显示参数φ在不同样本长度下的均方误差MSEφ(t).由图3可知当样本量为50时,参数的均方误差普遍较大,随着样本量增大,各个时刻的均方误差MSEφ(t)逐渐减小;另外,在样本量较小时,时间t=0.8,1.7左右处的均方误差较大,而在时间t为0.2和1.3左右处MSEφ(t)最小.与图2对应来看,即当|φt|较大时,其估计量的均方误差也较大;当|φt|较小时,其估计量的均方误差也较小.但当样本量较大时,这种现象则不明显.另外,bφt位于时间区间边界处估计的均方误差改善效果略差于处于区间内部的参数.

图3 在不同样本长度下参数φ的MSEφ(t)Fig.3 MSEφ(t)of φ for dif f erent length of samples
图4和5分别描述了在不同样本长度下参数φ的全局均方误差GMSEφ和σ的均方误差MSEσ均随样本长度的增大而减小.特别是当从小样本开始增加样本时,下降幅度较大.当样本长度继续增大时,其下降速度逐渐变缓,这与图3显示的信息是一致的.在实际应用中,如果样本长度取的过大,则bφ和b σ的表达式(10),(11)中的n−1维矩阵A的阶数会很高,计算量将大大增加.因此考虑到计算负担及实际可获得样本长度的情况,通常在计算负担与估计效果之间权衡,进而选取适当的样本长度.

图4 在不同样本长度下参数φ的GMSEφFig.4 GMSEφ of φ for dif f erent length of samples

图5 在不同样本长度下参数σ的MSEσFig.5 MSEσ of φ for dif f erent length of samples
3 实证分析
人均GDP是一个国家经济发展的综合表现.由于人均GDP的波动受到经济环境和政治环境等多方面因素的影响,因此不存在恒定的内在规律来描述这种波动,可以认为其增长变化是动态的.为了反映这种动态变化,本工作对我国人均GDP增长率情况建立了一阶时变自回归模型,并将估计结果与实际情况进行了对比分析(见图6).样本选取1952—2014年我国人均GDP序列Gn[12](见图7),n=1,2,···,63,其年增长率
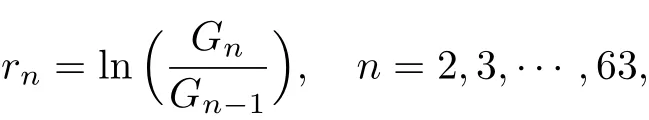
xn为rn的中心化变量,


图6 人均GDP年增长率Fig.6 Annual growth rate of capita GDP
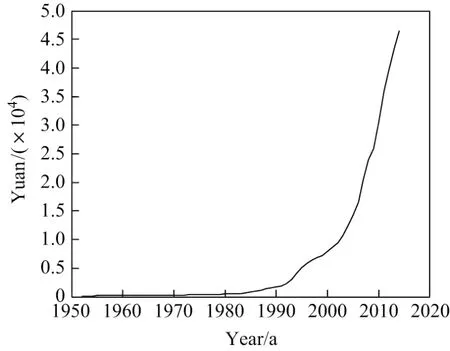
图7 1952—2014年我国人均GDPFig.7 Capita GDP of China during 1952—2014
对xn建立一阶时变系数自回归模型:
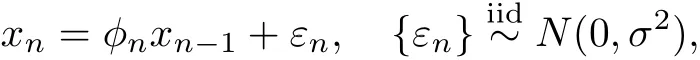
φ与σ的先验分布为式(3),为了充分利用样本信息,把上一次计算得到的后验均值作为下一次计算的先验均值,即=0,=m(k−1),k>1,m(k−1)是第k−1次后验均值.最终得到φ的贝叶斯估计值(见图8)和σ的贝叶斯估计值 σb=0.062 3.

图8 φn贝叶斯估计值bφnFig.8 Bayesian estimationbφnof φn
图8中,φn是我国人均GDP增长率变化的控制参数,其变化趋势显示在20世纪50年代人均GDP呈快速增长态势,在20世纪60年代至70年代呈停滞状态,甚至出现下降的情况,到了20世纪70年代后期则出现转机,φn开始提升,使得人均GDP出现了新一轮快速增长,φn在20世纪90年代中期到达顶峰.
图8所描述的我国人均GDP控制参数的变化状况与我国国情基本吻合.在20世纪50年代,我国开始实施计划经济建设,集中力量优先发展重工业.因此,在该阶段我国人均GDP增长速度较快,但是因为基数较低,所以在图7中反映不明显.到了20世纪60年代和70年代,我国在探索经济建设的道路上出现偏差,使得国民经济比例失调,对经济建设造成了巨大的破坏,经济发展处于停滞状态.这一点从估计值cφn在20世纪60至70年代中期的形态中可以看出.自1978年以来,我国实行改革开放政策,加快了国际经济一体化进程,进入了经济起飞阶段.我国经济迅猛发展的势头一直保持到20世纪90年代中期,之后我国经济增长的速度逐步调整到平稳状态.1995年以后,由于总人口增长速度减慢、资本的报酬收益递减及结构变革为经济增长所提供的动力日益减少等原因,我国经济增速步伐放缓.因此,总体来说,图8中显示的贝叶斯估计值bφn的波动情况与我国经济波动情况基本一致.
如果对xn建立定常AR(1)模型:
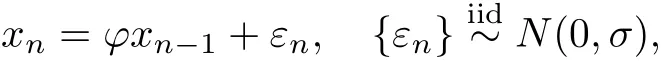
AR(1)的参数估计分别为b ϕ=0.607 7,b σ=0.064 8.
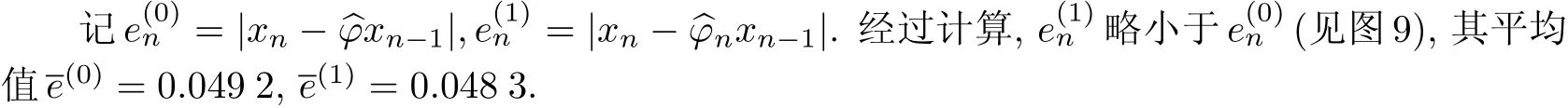

图9 xn在AR(1)模型下和TVAR(1)模型下的一步预测误差的绝对值Fig.9 Absolute errors of one-step prediction for xnfollowing AR(1)and TVAR(1)respectively
AR(1)与TVAR(1)模型的一步预测误差相差不大,但后者能更清晰地反映出经济波动现象背后的内在规律性.
4 p阶时变自回归
对于p阶时变自回归动态模型(1),记

则给定参数Φ,σ以及x0=(x1,x2,···,xp),样本x=(xp+1,xp+2,···,xn)的概率密度函数为

设σ服从倒Γ分布:

在给定σ下,Φ|σ~N(n−p)×p(M,W⊗V),W和V为对称正定阵,其中W=σ2S,且S和V均与σ 无关.令φ=(φp+1,1,φp+1,2,···,φp+1,p,···,φn,1,φn,2,···,φn,p)′,则样本x,参数Φ 和σ 的联合密度函数即为样本x,参数φ和σ的联合密度函数:
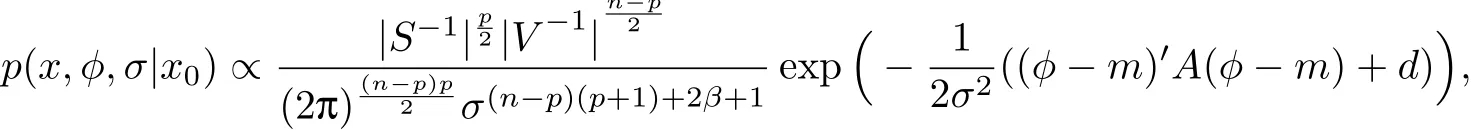
式中,

最终可以得到φ和σ的后验分布:
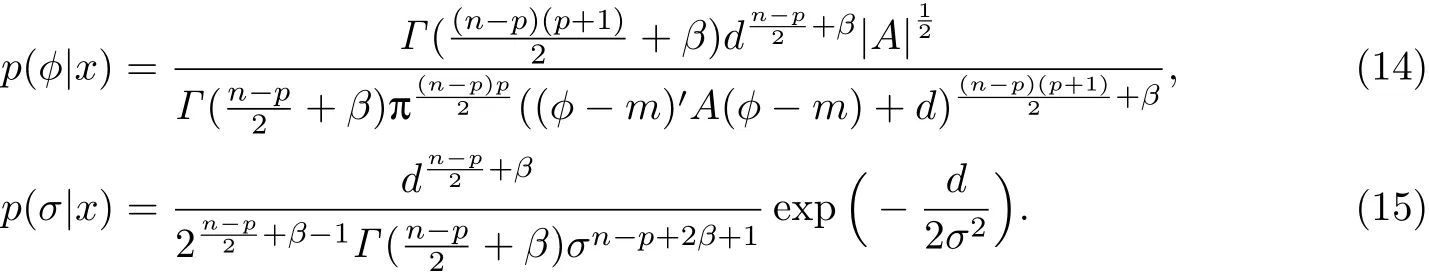
在二次损失下,φ的贝叶斯估计为

σ的贝叶斯估计为

5 结束语
本工作的研究对象为时变自回归模型,对于时变系数φt,本模型除在不同时刻下有一定相关性的假设外,没有附加过多的限制或假设条件.为使得在仅有一条样本信息的情况下仍可以得到较好的估计结果,本工作采用贝叶斯估计方法.实证分析表明,通过贝叶斯方法得到的估计结果能较好地描述实际问题的内在规律,相比于时不变(定常)系数模型具有更高的精确度.这是因为时变系数模型具有较高的灵活性,可在每个时刻用最合适的模型系数进行拟合.
[1]DAHLHUAUS R.Fitting time series models to nonstationary processes[J].The Annals of Statistics,1997,25(1):1-37.
[2]WEST M,PRADO R,KRYSTAL A D.Evaluation and comparision of EEG traces:latent structure in nonstationary time series[J].Journal of the American Statistical Association,1999,94(446):375-387.
[3]PRADO R,HUERTA G.Time-varying autoregressions with model order uncertainty[J].Journal of Time,2002,23(5):599-618.
[4]BIbI A,FRANCq C.Consistent and asymptotically normal estimators for cyclically timedependent linear models[J].Annals of the Institute of Statistical Mathematics,2003,55(1):41-68.
[5]FRANCq C,GAUTIER A.Estimation of time-varying ARMA models with Markovian changes in regime[J].Statistics and Probability Letters,2004,70(4):243-251.
[6]TRIANTAFYLLOpOULOS K,NASON G P.A Bayesian analysis of moving average processes with time-varying parameters[J].Computational Statistics and Data Analysis,2007,52(2):1025-1046.
[7]NAkAjIMA J,KASUYA M,WATANAbE T.Bayesian analysis of time-varying parameter vector autoregressive model for the Japanese Economy and Monetary Policy[J].Journal of the Japanese and International Economies,2011,25(3):225-245.
[8]IjIMA H,GRIvEL E.Deterministic regression methods for unbiased estimation of time-varying autoregressive parameters from noisy observations[J].Signal Processing,2012,92(4):857-871.
[9]王永民,何幼桦,忻莉莉,等.时变自回归模型系数的估计及预测[J].应用数学与计算数学学报,2007,21(2):35-41.
[10]BEkIROS S.Forecasting with a state space time-varying parameter VAR model:evidence from the Euro area[J].Economic Modelling,2014,38(C):619-626.
[11]BARNETT A,MUMTAZ H,THEODORIDIS K.Forecasting UK GDP growth and inf l ation under structural change:a comparison of models with time-varying parameters[J].Bank of England Quarterly Bulletin,2012,89(3):1237-1246.
[12]中华人民共和国国家统计局National data—–国家数据[EB/OL].[2015-12-30].http://data.stats.gov.cn/easyquery.htm?cn=C01.
Bayesian estimation of autoregressive models with time-varying coefficients
CHEN Yunxian,GAO Xingyue,WANG Yuying,HE Youhua
(College of Sciences,Shanghai University,Shanghai 200444,China)
This paper analyzes a time-varying autoregression model where coef f cients are correlated at dif f erent time.When only one sample path is chosen,the Bayesian method is used for estimation.Formulas of estimation of the f i rst order model are presented.This paper also discusses how the estimation is af f ected by the coef f cient values and the length of samples.To conclude,based on an empirical evidence,it is shown that the statistical results are consistent with the actual data.
time-varying coef f cients;autoregressive model;Bayesian estimation;per capita GDP
O 212
A
1007-2861(2017)05-0732-10
10.12066/j.issn.1007-2861.1754
2016-03-16
国家自然科学基金资助项目(11371242)
何幼桦(1960—),男,副教授,博士,研究方向为概率论与数理统计.E-mail:heyouhua@shu.edu.cn

