长周期地震动下大跨斜拉桥随机地震反应对比

张 婷

(上海同豪土木工程咨询有限公司，上海 200092)

长周期地震动下大跨斜拉桥随机地震反应对比

张 婷

(上海同豪土木工程咨询有限公司，上海 200092)

长周期地震动下大跨桥梁的抗震性能研究备受关注。以某超大跨斜拉桥为研究对象，建立ANSYS三维有限元模型，利用改进虚拟激励法，进行长周期和普通地震动作用三向激励下对比分析。结果表明：两类地震动三方向激励对该桥响应特性的影响规律大体相同，且长周期地震动作用下该斜拉桥的内力和位移响应明显大于普通地震动下的响应值。

长周期地震动；功率谱密度；斜拉桥；改进虚拟激励法；数值对比分析

0 引言

随着大跨桥梁、体育场馆和高层建筑等超大超高复杂结构的大量兴建，这些具有长周期性质的建筑物因共振现象，在长周期地震动作用下，破损加剧、甚至倒塌。例如1995年日本阪神发生7.3级地震，主跨为485 m一座钢结构斜拉桥发生了局部破坏[1]；1996年我国黄海发生6.1级地震，上海东方明珠电视塔部分消雷器被震断；2008年我国汶川发生8.0级地震，死伤惨重，大量桥梁和房屋严重被毁坏[2]。因此，对大跨桥梁结构开展长周期地震动下抗震性能研究意义重大。需要说明的是，本文并非是从地震学角度，而是从工程角度上的长周期振动[3]。

目前，大跨桥梁结构地震反应研究的重点集中于普通地震动作用下的分析。秦权等[4]利用生成的非一致地震人工地面加速度时程作为输入，对苏通大桥进行了多点激励下地震反应研究；Wang等[5]对4座连续梁桥，进行了多种工况(桥墩高度、激励方向和视波速的不同)下的弹塑性行波效应研究；闫聚考等[6]利用有限元软件SAP2000对泰州长江大桥进行了考虑行波效应的地震响应分析，并与振动台试验结果作对比。

研究以文献[7-8]基于大量强震记录，选用Clough-Penzien模型，采用最小二乘法拟合求取的长周期与普通地震动功率谱密度函数为输入，借助ANSYS软件建立某超大跨斜拉桥三维有限元模型，采用改进虚拟激励法，对该斜拉桥进行了两类地震动三方向激励下的随机地震响应对比分析。

1 随机地震反应分析原理

1.1随机地震动场模拟

多点激励随机振动分析中，空间地震动模型在频域内可表达为[9]：

(1)

其中，Sjj(ω)为自功率谱；Cjk(ω)和Qjk(ω)分别为互功率谱的实部和虚部。

地面任意两点的互功率谱可由各点自功率谱表示为[10]：

(2)

其中，|ρkl(iω)|和exp[iθkl(ω)]分别反映了相干效应和行波效应的影响，而和体现了场地k点和l点的局部场地效应。

1.2结构峰值响应计算

直接利用随机振动反应的各阶谱矩进行结构设计和研究还不够直观，一般通过响应量的各阶谱矩估计出响应极值的均值和方差来体现结构响应的大小。目前计算结构响应均值和方差较为普遍的方法是Davenport所提出的方法[11]，具体计算过程如下：

令随机反应绝对值X(t)在时间[0，T]内的最大值可表示为：

(3)

其均值和方差分别为：

(4)

式中，γm、△m称为峰值因子，公式如下：

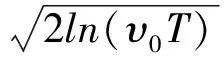
(5)

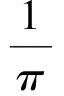
2 大跨斜拉桥有限元模型及动力特性分析

以某漂浮结构体系的双塔双索面斜拉桥为研究对象。主桥跨径及结构布置如图1所示，主梁采用封闭钢箱梁，其上翼缘为正交异性板结构，含风嘴全宽41.0 m，中心线处高度为4.0 m；桥墩选用灌注群桩基础；索塔采用人字形钢筋混凝土结构，承台以上高为300 m；斜拉索采用高强度平行钢丝拉索，共272根。

图1 主桥跨径及结构布置图

ANSYS软件建立的有限元模型如图2所示。全桥各部位所采用的模拟单元如下：主梁、桥塔及墩(BEAM44)、斜拉索(LINK10)、二期恒载及附加质量(MASS21)。借助Ernst公式修正斜拉索的弹性模量[12]，以此考虑斜拉索垂度的影响。主梁与桥塔横向主从约束，其它向均自由；主梁与桥墩纵向自由，其它向均约束。

图2 大跨斜拉桥有限元模型

振动阶数频率/Hz振动阶数频率/Hz10．079110．50120．125120．52330．183130．56940．232140．60250．338150．62860．360160．65670．395170．68580．430180．69790．469190．711100．486200．725

采用子空间迭代法对该斜拉桥进行结构动力特性分析。限于篇幅，表1仅给出前20阶自振频率。由表可见，一阶频率可求出一阶周期为12.67 s，该桥具有长周期性质；自振频率属密集分布，且变化较均匀。振型分析结果表明：一阶振型为主梁纵漂，体现了漂浮体系基本特点；二阶及三阶振型分别为主梁对称横弯和对称竖弯；四阶振型为主梁反对称竖弯；结构振型具有显著的三维耦合性。

3 结构随机地震反应对比分析

为了考察不同地震动功率谱作用下超大跨斜拉桥随机地震响应的情况，选取基于Clough—Penzien随机地震动模型拟合的长周期与普通地震动软土场地的平稳功率谱密度曲线作为输入，如图3所示；相应的拟合随机地震动模型参数见文献[7-8]。借助ANSYS有限元软件，采用直接求取位移的改进虚拟激励法[13-14]，对该斜拉桥进行了长周期与普通两类地震动三向激励下(纵向+横向+竖向)随机地震响应对比分析。

图3 两类拟合功率谱密度函数曲线

按7度抗震设防、III类场地进行分析。在考虑三向地震分量共同作用时，X、Z和Y方向的加速度峰值的比例为1:0.85:0.65，则X、Z和Y方向的自功率谱密度的比列为1:0.7225:0.4225[15]；由此可计算出X、Z和Y三个方向的自功率谱密度(长周期：0.004 m2/3、0.00289 m2/3、0.00169 m2/3；普通：

0.003 m2/s3、0.00217 m2/s3、0.00127 m2/s3)。并根据结构的自振频率，确定了有效频域积分区间为ω∈[0.5,90.0]rad/s，积分间隔为0.05 rad/s。

两类地震动下该桥主梁在三向地震激励时不同位置处内力及位移响应最大值的均值图，如图4和图5所示。两类地震动下该桥左塔在三向地震激励时不同位置处内力及位移响应最大值的均值图，如图6和图7所示。由于左右桥塔响应规律较为相似，且限于篇幅，本文仅给出了左桥塔的响应结果。

(a)扭矩(Mx)最大值均值

(b) 横向弯矩(My)最大值均值

(c) 纵向弯矩(Mz)最大值均值

(d) 竖向剪力(Fy)最大值均值

(e) 横向剪力(Fz)最大值均值

(a) 竖向位移(Uy)最大值均值

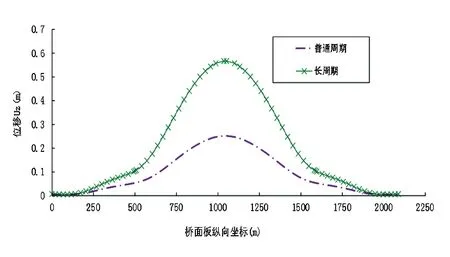
(b) 横向位移(Uz)最大值均值

(a) 横向弯矩(Mx)最大值均值

(b) 纵向弯矩(Mz)最大值均值

(c) 纵向剪力(Fx)最大值均值

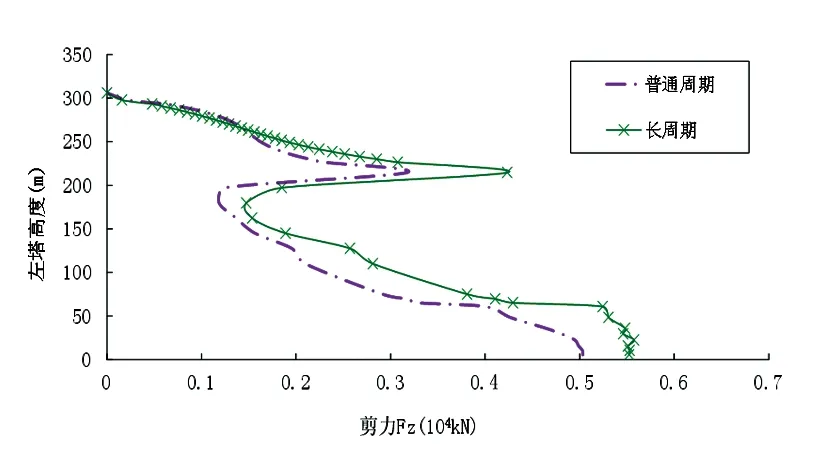
(d) 横向剪力(Fz)最大值均值

(a) 纵向位移(Ux)最大值均值

(b) 横向位移(Uz)最大值均值

由图4可知，两类地震动下主梁内力响应的规律大体相同，沿桥面纵向呈现多个峰值。扭矩(Mx)在桥塔处达最大值，且长周期地震动下的约为普通地震动下的1.6倍；横向弯矩(My)在两桥塔处及主跨跨中位置均出现较大的峰值；纵向弯矩(Mz)在主跨跨中处，长周期地震动下为9.96×104kN，而普通地震动下仅为5.98×104kN；竖向剪力(Fy)在左右辅助墩处达到峰值，长周期地震动下分别为0.51×104kN和0.62×104kN；横向剪力(Fz)在两桥塔处出现最大峰值，长周期地震动下的约为0.38×104kN。

由图5可得，两类地震动下主梁位移响应最大值均出现在桥面板主跨跨中位置，边跨部分的位移值相对较小。长周期地震动作用下竖向位移(Uy)和横向位移(Uz)峰值分别为和，均明显大于普通地震动下的位移响应。

从图6可看出，两类地震动下桥塔内力响应沿塔高的减小均呈现逐渐增大的规律，横向弯矩(Mx)在桥塔倒Y形索塔分岔点处、桥塔横梁处以及塔底均出现比较大的峰值。纵向弯矩(Mz)在塔底处达到最大值，长周期地震动下为7.8×105kN，约普通地震动的1.5倍。纵向剪力(Fx)和横向剪力(Fz)在长周期地震动下塔底处达最大值，分别为0.55×104kN、0.54×104kN。

由图7可表明，两类地震动下桥塔位移响应沿塔高的增大呈现逐渐增大的趋势，塔顶处达到最大值，纵向位移(Ux)及横向位移(Uz)长周期地震动下最大响应分别约为普通周期地震动下的2倍。

4 结论

由结构动力特性分析可得出，该斜拉桥存在较强的三维运动耦合性，在对大跨斜拉桥进行随机振动分析时有必要考虑三个方向共同作用。

通过分析可知，两类地震动下主梁最不利受力断面出现的位置基本一致，主要位于两桥塔处、主跨跨中、主跨四分点处、边跨距桥塔处、边跨辅助墩处；桥塔最不利受力断面主要位于塔顶截面、倒Y形索塔分岔点处、桥塔横梁处截面、塔底截面。

算例中两类地震动功率谱三向作用下主梁和桥塔内力及位移响应变化趋势大体相似，但长周期地震动作用下的结果明显大于普通地震动作用下的，故具有长周期特性的大跨结构考虑长周期地震动作用是非常有必要的。

[1] 李春锋,张旸.长周期地震动衰减关系研究的迫切性[J].地震地磁观测与研究,2006(3):1-8.

[2] 庄卫林,刘振宇,蒋劲松,等.汶川大地震公路桥梁震害分析与对策[J].岩石力学与工程学报，2009(7):1377-1387.

[3] 谢礼立,周雍年,胡成祥,等.地震动反应谱的长周期特性[J].地震工程与工程振动,1990(1):1-19.

[4] 秦权,孙晓燕,贺瑞,等. 苏通桥对非一致地震地面运动的反应和人工波质量的讨论[J].工程力学,2006(9):71-83,188.

[5] WANG J, CARR A J, COOKE N, et al. The response of a 344m long bridge to non-uniform earthquake ground motions[J].Engineering Structures, 2009(11):2554-2567.

[6] 闫聚考,李建中,彭天波,等.三塔两跨悬索桥行波效应振动台试验及数值研究[J].振动与冲击,2016(7):44-48,55.

[7] 陈清军,张婷,陈志海,等.长周期随机地震作用下超大跨斜拉桥的行波效应分析[J].湖南大学学报,2014(4):1-9.

[8] 张婷. 长周期随机地震动模拟与大跨桥梁结构地震反应研究[D].上海:同济大学,2015.

[9] JIA H Y, ZHANG D Y, ZHENG S X, etal. Local site effects on a high-pier railway bridge under tri-directional spatial excitations: Nonstationary stochastic analysis[J]. Soil Dynamics and Earthquake Engineering,2013(52):55-69.

[10] 林家浩，张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004.

[11] DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Procceeding Institution Civil Engineering, 1961(2):187-196.

[12] 范立础. 桥梁工程[M].北京:人民交通出版社,2012.

[13] 李永华, 李思明. 绝对位移直接求解的虚拟激励法[J].振动与冲击,2009(10):85-190.

[14] 贾宏宇, 郑史雄.直接求解多维多点地震动方程的虚拟激励法[J].工程力学,2013(3):341-346.

[15] 丁阳, 林伟, 李忠献.大跨度空间结构多维多点非平稳随机地震反应分析[J].工程力学,2007(3):97-103.

ComparativeAnalysisofLong-spanCable-stayedBridgeunderLong-periodStochasticSeismicExcitation

ZHANG Ting

(Shanghai Tonghao Civil Engineering Consulting Co., Ltd.Shanghai 20092,China)

Seismic response of a long-span cable-stayed bridge under long-period and general earthquake motions has been paid close attention. In the paper, some super-long-span cable-stayed bridge is taken as a case study whose three-dimensional finite element model is established in ANSYS. Then a comparative analysis of the bridge under long-period and general earthquake motions in three directions is performed using improved pseudo-excitation. Results show that similar patterns arise for the response characteristics of the bridge under three directional excitations, in addition the response of internal force and displacement under long-period earthquake motions is distinctly larger than that under general earthquake motions.

long-period ground motion; power spectral density; cable-stayed bridge; improved pseudo-excitation method; digitally comparative analysis

TU311.3；TU997

A

1009-7961(2017)05-0057-05

2017-07-20

张婷(1983-),女，安徽宣城人，助理工程师，博士，主要从事桥梁抗震性能研究。

(责任编辑：孙文彬)