基于ADE7878的零序电流相位角计算方法研究

秦亚杰，朱建良，薄煜明，吴盘龙

基于ADE7878的零序电流相位角计算方法研究

秦亚杰，朱建良*，薄煜明，吴盘龙

(南京理工大学 自动化学院，南京 210094)

单相接地故障是电力系统配电网络中故障发生的主要原因之一。针对通过零序电流大小判断单相接地故障的局限性，为了有效快速隔离配电网单相接地故障点，研究通过零序电流相位角来判断故障点所在位置区间的方法。通过ADE7878读取三相电流以及三相电压的瞬时值，分别使用全周积分算法和全波傅里叶算法来处理数据，得到零序电流、电压的实部和虚部，求取夹角得出相位角的大小。结果表明，全波傅里叶算法得出的数据误差标准差比前者降低了80%，面对复杂的电力系统，该算法可以更为有效处理三相电能数据，符合微机保护准确性和可靠性的要求，在电力系统网络故障隔离中有关键作用。

ADE7878；相位角；全周积分算法；全波傅里叶算法

0 引言

随着电力系统的不断发展，继电保护的设备及技术也有了长足的进步与提高，常规的继电器保护越来越不能满足现今电网发展的需求，而综合的微机保护发挥的作用将越来越大。

电力系统配电网络结构复杂且故障多发，单相接地故障也是故障发生的主要原因之一[1]。虽然发生单相接地故障后，系统还能够继续运行一段时间，供电可靠性相对较高，但是接地故障产生的过电压还是会对系统产生威胁，甚至有可能中断正常供电。为了迅速解决此类问题，我们必须要快速准确隔离故障地点，零序电流相位角将是判断故障地点的重要依据[2-3]。

一般方法中三相电流和电压的采集多采用芯片采集到的有效值，此次研究使用的方法将是采集计量芯片ADE7878中的三相电流和电压的瞬时值。对正弦交流量的处理多以全波积分算法居多，但是电力系统复杂多变，通过与全波傅里叶算法的对比来得到更适合计算相位角的方法[4]。为了实现系统三相电流与三相电压的瞬时值采样，实际采用NXP公司出产的LPC2366芯片，配合采样芯片ADE7878来完成。考虑到软件复杂程度和采样精度及MCU芯片和综合计量芯片的性能，控制器采用每工频周期采样40点，不仅保证了软件处理的快速性，还保证了测量的精度。计算结果对照表明，利用傅里叶算法处理采集到的数据能计算出更准确的零序功率相位角[5]。

1 ADE7878计量芯片

ADE7878是一款三相电能专用计量芯片。该器件采用串行接口，提供三路灵活的脉冲输出，且输出精度高，功能多样。内置基准电压源电路、数字积分器、二阶Σ-Δ型ADC以及所有必需的信号处理电路，ADE7878可以执行有效值计算，以及各相及合相全波无功功率、有功功率、视在功率、基波无功和有功功率测量。该芯片是通过一个固定功能数字信号处理器(DSP)来执行这种信号处理。

三角形或Y形等三线、四线的三相配置无功功率、有功功率和视在功率都适合用ADE7878来测量。各相均具有增益校准、相位校准和有效值失调校正等系统校准功能。CF1、CF2和CF3逻辑输出可提供无功功率、有功功率、电流有效值和或总视在功率等功率信息。ADE7878允许访问所有ADC输出，具有波形采样寄存器。该芯片还提供瞬时高电流变化、瞬时低压或高压检测、相电压与电流之间的角度以及线电压周期测量等电能质量监测状态。除此之外，ADE7878芯片还提供了一个SPI接口用来方便与外部MCU之间进行计量参数读取[6]。

2 系统硬件设计

该系统硬件设计主要包含采样电路ADE7878、串口通信模块、GPRS模块、控制继电器线圈的IO输出、状态IO输入以及控制开关的IO输出设计。

接下来主要是高精度功率计量芯片ADE7878采样电路的设计与实现，三相电压、三相电流的瞬时值等工频量信息采样主要通过主控芯片LPC2366与ADE7878通过SPI总线进行读取与计算。

芯片ADE7878的输入交流电压信号不能大于500 mV，所以需要对输电线路上的大电压以及大电流进行调理变换。在ADE7878芯片的采样电路设计中，电流的输入采样要先经过电流互感器的耦合,再通过精密电阻R1、R2转换成不超过500 mV以内的差分交流电压信号。二极管D1主要防止电压过大损坏芯片。信号输入过程中还存在高频噪声信号，通过R3、R4、C1以及C2组成的阻容抗混叠滤波电路来进行滤波处理。经过滤波之后的信号再输出到ADE7878的电流信号输入端。对电压的输入采样首先要经过定值精密电阻R0转换成弱电流信号，之后在经过电压互感器的耦合得到同频同相的交流电流信号。然后再通过调理电路将交流电流信号转换成差分电压。最后再经过抗混叠滤波后输出到ADE7878的电压信号输入端。这种电流电压的输入采样方式让芯片与电网隔离，保证了电路的抗干扰性能。

3 算法原理

采样算法和滤波算法是三相电压与电流的采集主要考虑的两个方面，目的是滤除电能信号质量不确定的线路上的噪声分量，保证能够快速并准确地采样得到需要的电气量参数。应用何种软件算法主要考虑计算精度和计算速度这两个方面。其中，计算速度包括算法需要的运算工作量以及算法要求的采样点数(或称为数据长度)。平衡矛盾的精度和速度是软件算法的研究的主要方面。一般情况下，采样点数越多，采样精度也越高，但是采样点数增多会增加运算工作量，所以选取合适的算法需要结合实际的保护情况来确定。

此外，为了滤除线路上可能出现的噪声信号和高次谐波，控制器还需要选用合适的滤波算法，否则采样精度会降低，而且对于一些快速动作的保护可能由于噪声信号而产生误动作。有一些采样算法同时具有数字滤波功能，在实际工业应用中应用广泛。

3.1采样点数的选择

为了完成系统三相电流电压信号的采样，实验配合采样芯片ADE7878，采用NXP公司出产的的LPC2366芯片。LPC2366芯片为Cortex-M3架构，该架构CPU具有3级流水线和哈佛结构，除了拥有独立的数据总线与本地指令总线，还有用于外设的性能略低的第三条总线。为了使Flash中代码执行达到最佳性能，LPC2366还增加了一个专用的Flash加速器。ADE7878是一块外接的多功能高精度三相电能专用计量芯片，LPC2366一般情况下的操作频率最高可以达到120 MHz，两者通过SPI接口与MCU进行参数传递，通讯速率可达10 Mbps。

综合考虑采样精度和软件复杂程度及对MCU芯片和计量芯片的性能，为了保证了测量的精度和软件处理的快速性，控制器采用每工频周期采样40点。

3.2全周积分算法

因为一个正弦量在任意一个周期内的绝对值的积分为一个常数S,且积分值S与积分起始点以及初始角α没有关系，所以交流正弦量一般用全周积分算法来处理[7]。首先通过ADE7878采样得到当前电量瞬时值，以任意一相电流为例，电压同理，该相电流在任意一个周期内的绝对值的积分计算公式为

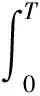
(1)

式中,(ω,t,α)是正弦量的相位,α称为正弦量的初相角,ω称为角频率。

电流有效值值可表示为

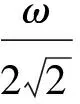
(2)

通过梯形法求和算出一个周期面积S常数

(3)

式中，ik为第k次采样点，k=0时采样值为i0，一周期的采样点数为N。

然后通过以上公式得到的三相电流可以计算零序电流和零序电压的实部与虚部(零序电压的实部和虚部计算同理)：

(4)

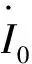
(5)

因为在全周积分中高频分量叠加在基波成份上的幅度不大，其对称的正负全周可以互抵消，剩下没有被抵消的部分占比很小，所以全周积分算法可以滤除一定的高频分量。但是全周积分算法不能抑制直流分量，这种算法运算工作量很小，需要的采样点数可调，非常简单的硬件就可以实现。

3.3全波傅里叶算法

通过计量芯片采集到的电能信号理论上是正弦波，但是有很多直流分量和各次谐波分量。傅立叶算法来源于傅立叶级数，基本原理是将周期函数分解为正弦和余弦分量，它适用于处理周期性的时间函数[8]，就是将一个周期性输入函数I(t)用傅立叶级数展开各次谐波的正弦项和余弦项之和，可表示为

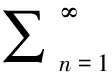
(6)

式中,n为自然数，n=0,1,2,3…表示谐波分量次数。电流中的基波分量i1(t)可以表示为

i1(t)=a1×sin(ω1t)+b1×cos(ω1t)

(7)

i1(t)还可以整理为

(8)

式中,α1t为t=0时基波分量的初相角，I1为基波有效值。用和角公式将sin(ω1t+α1)展开，可以得到I1和α1以及I1、a1和b1的关系。

a1=2I1×cosα1

(9)

b1=2I1×sinα1

(10)

从式(9)和(10)中可以看出要求得基波的有效值和初相位角α1，只要求出基波的正弦和余弦项幅值。

根据傅立叶级数的逆变换可求得a1和b1：

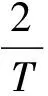
(11)

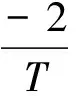
(12)

式中，T为基波分量周期。

将式(11)、(12)离散采样后可得：

(13)

(14)

式中,i(k)为k时刻的采样值，N为每基频周期内的采样点数。

这样就可以得到n次谐波的幅值为:

(15)

对采集到的三相电流和电压数据使用向量合成，得到的零序电压和电流实部和虚部，进而得到它们的的大小和方向。以零序电流为例(零序电压同理)，根据式(13)和(14)，且3P0n=PAn+PBn+PCn，采用全波傅里叶算法将三相电流离散，然后进行向量合成得到零序电流实部和虚部的算式为

(16)

(17)

其中，N为每周期内的采样点数，综合考虑LPC2366芯片的计算性能采用N为40，每全周期采样20点的方法进行计算。

同理计算零序电压实部和虚部，再根据上面计算得到的零序电流实部和虚部，然后求取夹角即相位角，最后通过相位角来判断零序方向。

通过这种方法得到的算式有较好的暂态性能。如果需要更快的动作速度,也可采用半波傅立叶算法求取零序电流的实部和虚部[9-10]。

3.4零序功率相位角计算

通过算法处理后得到零序电流和电压的实部和虚部，然后可以计算得出相位角的大小[11]。零序电压与零序电流相位角示意图如图1所示。

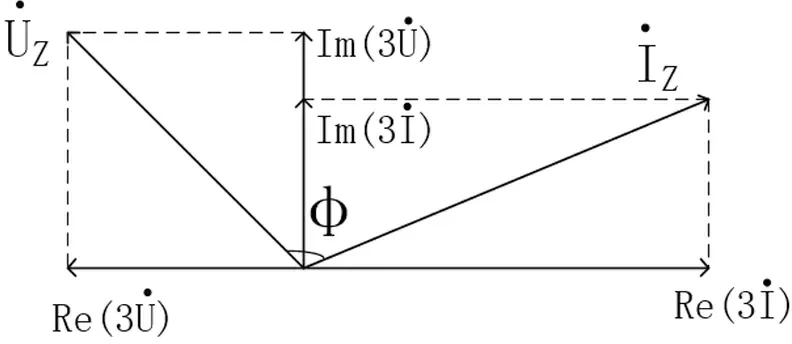
图1相位角示意图

令零序电流实部虚部分别为IRe、IIm,零序电压实部虚部分别为URe、UIm,零序零序电压与零序电流夹角计算公式为：

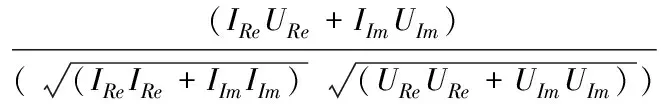
(18)

零序电压与零序电流相位角计算公式为：

(19)

4 实验结果与分析

为了验证全周积分算法和全波傅里叶采样算法处理读取的瞬时值的性能以及计算相位角的准确性，就要验证对比两种算法处理得到的相位角的大小。

实验采用南京丹迪克公司研发的DK-34B1交流采样变送器校验装置，它可以产生标准的工频正弦三相电流电压信号，将该设备将输出值分别调整为A相电流为4 A，B相电流为4 A，C相为2 A；A相电压为50 V，B相电压为100 V，C相电压为100 V。主控芯片LPC2366则在1000定时中断中读取ADE7878瞬时值寄存器，再通过两种算法分别计算得到的零序电流、电压的实部和虚部，最后计算得出相位角的大小。将计算后的结果均通过串口发送到上位机，读取数据，列出全周积分算法与全波傅里叶算法的结果对比。

根据处理后的三相电流与电压计算得出零序电流与零序电压的实部与虚部，从而计算得出相位角的大小，在设定值的基础上相位角理论值大小为 240°。

分别取全周积分算法与全波傅里叶算法处理后得到的相位角的100次数据，用Matlab绘图比较误差如图2。

图2全周积分算法与全波傅里叶算法处理后得到的相位角大小比较

相位角理论值与计算值及其误差比较如下表。表1比较两种算法得出的相位角与设定值比较的误差，全周积分算法得出的数据误差标准差接近1%，而全波傅里叶算法得出的数据误差标准差比前者降低了80%。

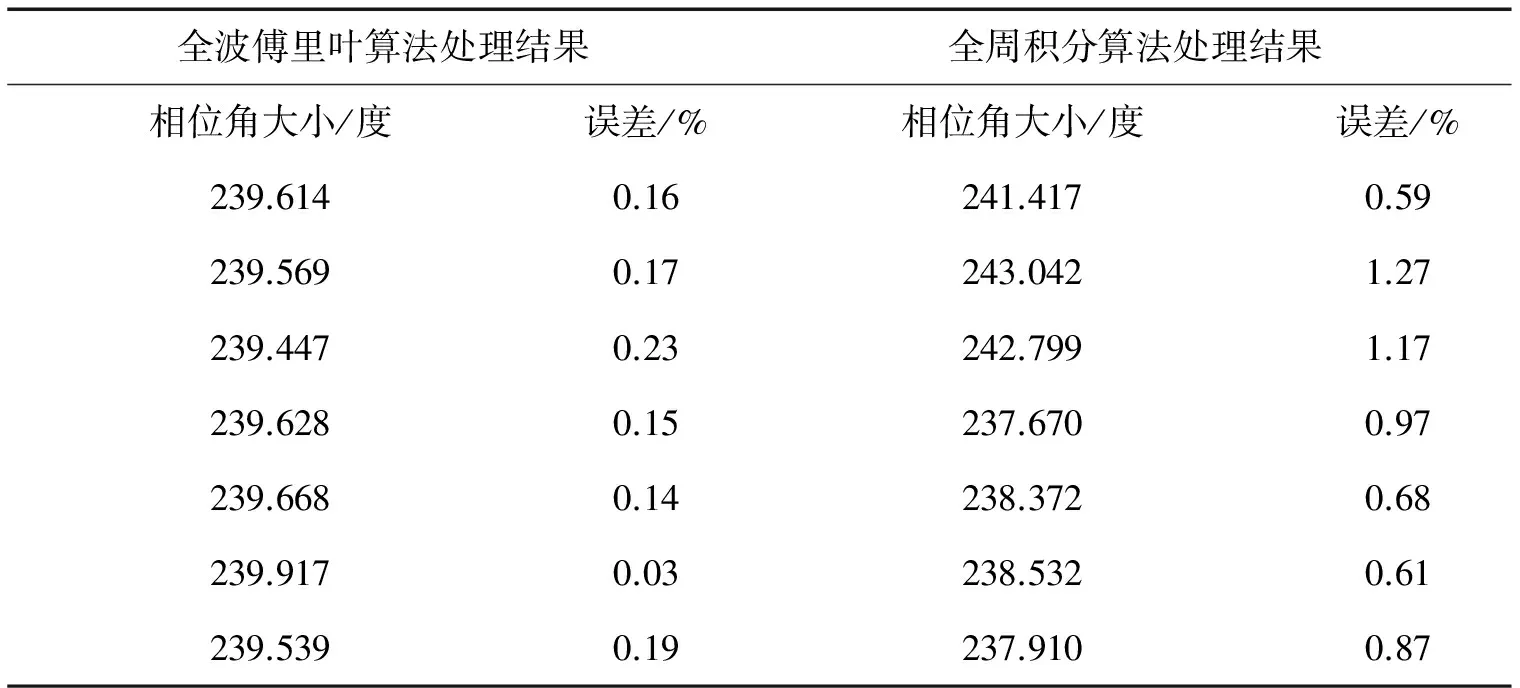
表1 相位角理论值与计算值对比

5 结论

根据ADE7878功率计量芯片的特点，考虑工程实际应用中对数据采集以及相位角计算准确性的要求，提出了利用全周积分算法和全波傅里叶算法处理所读取的ADE7878瞬时寄存器数值，并利用计算得出的零序电流、电压的实部和虚部计算得出了零序功率的相位角，结合以上方法在芯片LPC2366上进行了实验对比与验证。实验结果表明，全波傅里叶算法得出的数据误差标准差比前者降低了80%，且计算结果比较稳定。与全周积分算法相比较，傅立叶积分算法可以更广泛的用于计算各种周期性时间函数，还可以计算初相角。其积分运算结果同样可以抵消一个周期内的正负全周的高次谐波，同样具有数字滤波的功能，运算工作量也不大。全周积分算法是时域角度分析，傅里叶算法是从频域角度分析，电力系统数据复杂多变，后者可以更有效处理这些数据并得到准确的零序电流和电压的实部和虚部，以此来推算出的相位角准确且稳定，对电力系统网络故障隔离有重要意义。

[1] 徐永峰.中性点直接接地系统接地短路的零序电流及方向保护[J]. 黑龙江科技信息,2015(24):72-72.

[2] 陈曦,傅锦发,樊征臻,等.线路非全相运行及其再故障零序方向保护的动作特征分析[J].电力系统保护与控制. 2013(6): 82-88.

[3] 阿里木江·卡德尔,索南加乐,阿米那古丽·艾尼,等. 基于超高压自耦变压器中性点零序电流的方向比较纵联保护的研究[J]. 电力系统保护与控制,2014(22):24-31.

[4] 饶成诚,吴禹臻,王海云,等.110 kV线路零序电流方向保护校验及事故分析[J].电力学报. 2015(6):04-05.

[5] 程真何,刘桂林. 110 kV线路零序电流保护误动原因分析及对策[J]. 电测与仪表,2014(23):120-128.

[6] 马芸芸. 基于ARM和ADE7878的多功能电力监测装置[D].南京：南京理工大学，2012.

[7] 赵佳楠,张丕状. 基于半周期积分算法的微小振动测量研究[J]. 电子产品世界,2017(4):47-50.

[8] 刘益青,高伟聪,孙天德. 适用于数字化保护的改进递推傅里叶算法[J]. 电网技术,2016(5):1601-1606.

[9] 王晋,胡斌. 基于全波傅里叶算法的智能变电站谐波分析方法[J]. 湖北电力,2013(2):20-21.

[10] 张骁,肖岚,陈永华. 一种滤除衰减直流分量的全波傅里叶相角修正算法[J]. 佳木斯大学学报:自然科学版,2014(2):253-257.

[11] 潘清甫,刘靓. 相序坐标与零序电流相位测量[J]. 华中电力,2012(1):22-24.

ResearchonPhaseAngleCalculationMethodofZeroSequenceCurrentBasedonADE7878

QIN Ya-jie, ZHU Jian-liang*, BO Yu-ming, WU Pan-long

(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

The single-phase earth fault is one of the main reasons for the malfunction of power system distribution network in China. Since the use of zero-sequence current size to detect single-phase earth fault is limited, the method adopted in the research is judging fault point through zero-sequence current phase angle in order to isolate the single-phase earth fault points of the distribution network efficiently and quickly. First using ADE7878 to read the instantaneous value of three-phase current and three-phase voltage, then applying Full-Cycle Integral algorithm and Full Wave Fourier algorithm respectively to process data and get the real part and imaginary part of zero-sequence current and voltage, and finally calculating the included angle to get the phase angle. The experimental results indicate that the data error standard deviation from Full Wave Fourier algorithm is 80% lower. In the face of complicated power system, Full Wave Fourier algorithm can process three phase electric energy more effectively, meets the requirements of accuracy and reliability of microcomputer protection, and plays a key role in the power system network fault isolation.

ADE7878; phase angle; Full-Cycle Integral algorithm; Full Wave Fourier algorithm

TM77

A

1009-7961(2017)05-0023-05

2017-08-11

国家自然科学基金(61473153)；江苏省产学研联合创新资金-前瞻性联合研究项目(BY2016004-04)

秦亚杰(1993- )，男，江苏盐城人，在读硕士，主要从事电气自动化研究。*为通信作者。

(责任编辑：孙文彬)