筒仓仓壁摩擦对仓壁侧压力影响的研究
张 昭 ,刘克瑾 ,肖昭然 ,王世豪 *
(1.郑州市轨道交通有限公司,河南 郑州450002;2.河南工业大学 土木建筑学院,河南 郑州 450001)
筒仓仓壁摩擦对仓壁侧压力影响的研究
张 昭1,刘克瑾2,肖昭然2,王世豪2*
(1.郑州市轨道交通有限公司,河南 郑州450002;2.河南工业大学 土木建筑学院,河南 郑州 450001)
采用离散单元法模拟分析仓壁摩擦因数不同的筒仓在贮料和卸料工况下的仓壁侧压力变化。研究结果表明,卸料引发的仓壁峰值压力分布为筒仓结构设计的控制压力。随着仓壁摩擦因数的增大,超压因数呈增大的趋势,而筒仓侧壁的静止压力和卸料压力峰值均有减小的趋势,且摩擦因数对仓壁侧压力的影响程度随着深度的增加而增大。
筒仓;离散单元法;摩擦因数;侧压力
0 引言
筒仓具有仓容量大、占地面积小等优点,在贮存散体材料方面具有其他贮存构筑物不具有的优势。因此,目前国内外对筒仓的应用越来越多,应用范围也越来越广[1]。为保证筒仓结构在使用过程中的稳定性,对筒仓仓壁在贮料静止状态以及卸料过程进行受力分析、精确确定贮存材料的载荷尤为重要。
国内外大量试验数据[2-4]表明,在筒仓内散体物料的卸料过程中,筒仓侧壁受到的卸料压力峰值比贮料压力要大得多,大部分筒仓工程事故都是由这种过大的卸料压力引起的[5],因此,对筒仓仓壁受力的深入研究很有必要。近几十年来,世界各国专家对此进行了大量的研究,但由于筒仓卸料过程中颗粒的受力及运动太过复杂,所以目前并没有形成统一的计算理论。
20世纪70年代,Cundall提出用离散元的思想对刚性圆球的运动及其相互间作用进行模拟。离散元法可以对不同形状的颗粒材料进行模拟;它可以解决静力状态的问题,也可以解决动力状态的问题[6-7]。因此离散单元法在研究筒仓仓壁受力问题上有较大优势。目前,离散单元法在采矿、岩土等领域已被广泛应用。
徐泳等[8]采用颗粒离散元法模拟了平底仓的卸料过程,研究了颗粒材料模量对卸料特性的影响;俞良群等[1]利用其对筒仓装卸料过程中的力场和速度场进行了研究;陈长冰等[2]用PFC2D研究了筒仓卸料过程中储料的流动状态、颗粒间接触力以及侧壁压力的变化,并将模拟得到侧壁动、静压力与试验值比较,结果显示其吻合性很好。Kobylka等[3]通过离散元模拟和室内实验研究了仓壁内部附着物对侧压力分布的影响。Weinhart等[9]用离散单元法研究了粗粒度对模拟结果的影响。文献[1-3]都用实际模型验证了离散元法模拟仓筒卸载问题的可行性。Moysey等[10]用试验和离散单元对不同仓壁对相同贮料的摩擦力进行了研究。Li等[11]利用离散单元法研究了仓壁摩擦对卸料流动状态的影响。
作者基于离散元软件PFC对筒仓卸料过程模拟,研究在贮料及卸料工况下不同仓壁摩擦因数对卸料水平压力的影响,并探讨了在不同工况及不同深度下其影响的作用大小。
1 模型建立
为研究仓壁摩擦因数对筒仓卸料流动状态和卸料压力的影响,本文共建立3个模型仓,不同的模型仓只改变墙体的摩擦因数。根据《钢筋混凝土筒仓设计规范》(GB 50077—2003)墙体摩擦因数μ分别设为0.0、0.3及0.4,分别对应于理想状态、钢筒仓和混凝土筒仓对小麦的摩擦因数。墙体和球体的其他物理参数保持不变。为保证模拟结果的真实性,参考文献[12],贮料为小麦的模型参数选取见表1。

表1 模型参数Table 1 Model parameters
模型仓高1 m,直径0.5 m,出口直径0.1 m,颗粒直径5 mm。每个模型仓设立测墙共20个,左侧和右侧测墙各10个,左侧测墙从上到下依次编号1~10,右侧测墙从上到下依次编号11—20。仓体模型如图1所示。

图1 仓体模型Fig.1 Silo model
2 筒仓贮料模拟分析
为保证满仓静止状态的准确性,对不同仓壁摩擦因数的模型仓均采用中心进料的方法填至满仓,每个模型仓内储存颗粒数量一定,均为20 400个。满仓后,程序继续运行一定时步使颗粒不平衡力基本为零,并使测墙压力曲线为一定值,此时系统达到稳定状态。
稳定状态下,不同仓壁摩擦因数、仓壁各个高度侧压力与Janssen公式对应计算值对比如图2所示。
由图2可知,μ=0.3和μ=0.4的数值模拟结果与对应的Janssen公式计算值基本吻合,说明数值模拟结果可以反映筒仓的实际受力情况。对比不同仓壁摩擦因数的静止侧压力值发现,摩擦因数越大,同一高度仓壁所受的压力越小,这说明摩擦的存在均化了筒仓侧壁受力,对仓壁侧压力有积极的影响。

图2 静止状态下仓壁侧压力的数值模拟结果与Janssen值Fig.2 Numerical simulation results Vs.Janssen values of lateral pressure under static state
Janssen公式中,一定高度的仓壁侧压力与该高度的竖向压力呈正比,即该高度的竖向压力越大,其仓壁侧压力就越大。仓壁高的摩擦因数会对仓壁附近的颗粒产生竖直向上的摩擦力,减小其竖向压力,从而使仓壁侧压力减小。模拟结果与Janssen公式的这一推论一致。
3 筒仓卸料模拟分析
3.1 卸料过程仓壁侧压力
图3为不同仓壁摩擦因数卸料过程中对应侧压力的动态分布图。由图3可知,卸料过程中不同仓壁摩擦因数的筒仓仓壁侧压力的变化规律基本一致:随着卸料的进行,仓壁侧压力先增大到压力峰值,再逐渐减小,在增大和减小的过程中会出现震荡现象[13]。
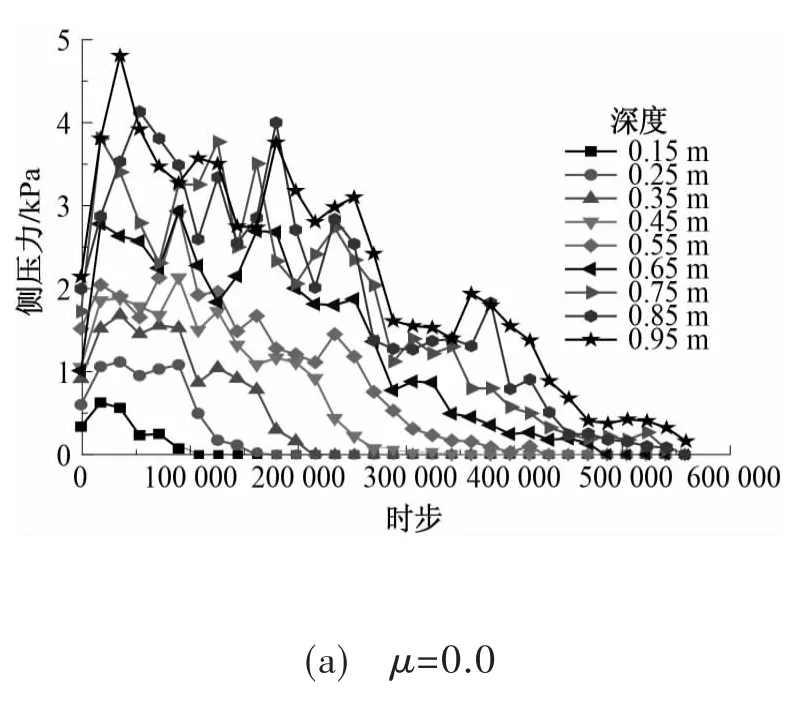

图3 卸料过程中仓壁侧压力Fig.3 Lateral pressure during discharge
由图3可知,卸料产生的侧压力峰值不是在卸料刚开始的时候出现的,而是在卸料进行一段时间之后才出现,这与肖昭然等[14]的研究结果一致。对比图3中(a)、(b)和(c)发现,在相同深度,仓壁摩擦因数越小,卸料产生的侧压力峰值越大。
3.2 仓壁摩擦对侧压力影响分析
为进一步研究仓壁摩擦因数对贮料工况和卸料工况下的侧压力的影响,定义一定深度的摩擦影响因数如下:

摩擦影响因数反映了不同摩擦因数在筒仓不同深度处对仓壁侧压力的影响大小,其数值越大,表明摩擦因数对仓壁侧压力的影响越大。贮料工况和卸料工况下的摩擦影响因数沿深度方向上的分布如图4所示。
由图4可知,贮料工况和卸料工况下,对于μ=0.3和μ=0.4的筒仓,随着贮料深度的增加,其摩擦影响因数总体均呈增大趋势。贮料工况下,在仓壁有摩擦的条件下,仓壁对附近的颗粒产生竖直向上,且正比于该深度侧压力的摩擦力。由Janssen公式可知,随着深度的增加,仓壁侧压力非线性增大,因此,仓壁对附近贮料产生的摩擦力也非线性增大。贮料工况下摩擦影响因数随深度增加而增大的趋势可能是由摩擦力的非线性增大引起的。
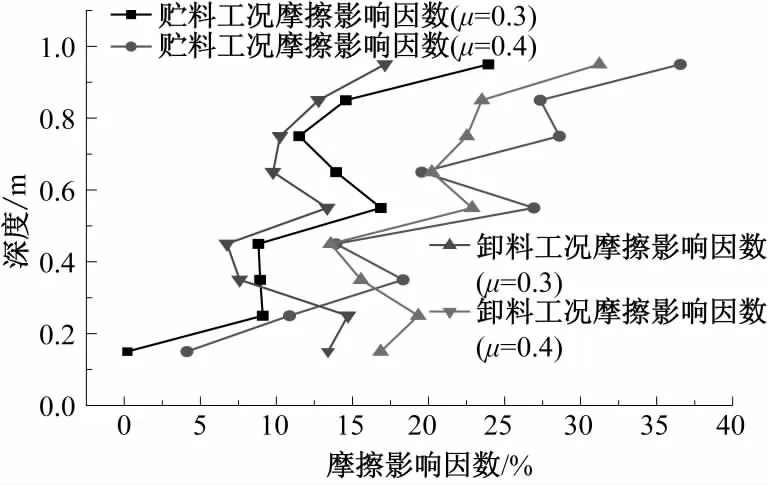
图4 摩擦影响因数Fig.4 Friction impact coefficient
对比图4中贮料工况下μ=0.3和μ=0.4的摩擦影响因数曲线发现,μ=0.4的摩擦影响因数均大于μ=0.3的仓壁摩擦因数。由静摩擦力的计算公式可知,在侧压力不变的条件下,仓壁对贮料产生的竖向摩擦力正比于仓壁和贮料的摩擦因数。因此,在贮料摩擦因数一定的条件下,仓壁摩擦因数越大(不大于贮料摩擦因数),仓壁附近贮料受到的竖向摩擦力越大,从而引起μ=0.4的摩擦影响因数较μ=0.3的大。
对比卸料工况下和贮料工况下的摩擦影响因数发现,对于相同仓壁摩擦因数的贮料压力和卸料压力峰值,仓壁摩擦因数在筒仓下部对侧压力的影响基本一致。但在筒仓上部,仓壁摩擦因数对卸料压力峰值的影响大于对贮料压力的影响。其中的内在机理还有待进一步研究。
3.3 贮料与卸料压力对比
将不同仓壁摩擦因数的动静压力的模拟结果与Janssen值和规范计算结果进行对比,同一高度的最大卸料压力与静压力的比值记为该高度超压因数。对比结果及超压因数见图5和图6。

图5 模拟静压力、卸料压力、Janssen值及规范卸料压力Fig.5 Static pressure,emptying pressure of simulation,Janssen value and code emptying pressure

图6 超压因数Fig.6 Overpressure coefficient
从图5可以看出,对于不同仓壁摩擦因数的模型仓,贮料压力和卸料压力峰值随着深度的增加而增加,其最大值均出现在筒仓底部附近[15-16]。对比相同深度的贮料压力和卸料压力发现,各个深度的卸料压力峰值都远大于对应的贮料压力值[2-417],且图6显示卸料压力峰值为贮料压力值的2~2.5倍。
由图5可知,仓壁摩擦因数越大,贮料工况下仓壁侧压力和卸料压力峰值越小,这与规范计算结果相吻合。但模拟结果显示,卸料压力峰值比规范计算结果大,对比图6,并结合筒仓结构失效的实例,说明规范选取超压因数可能偏小,尤其是对于仓壁比较光滑的筒仓。结合图5卸料压力曲线和图4发现,仓壁摩擦因数对筒仓下部卸料压力峰值的影响较上部更为明显。图6显示,超压因数在高度方向上分布无明显规律。对比不同仓壁摩擦因数对应的超压因数可以发现,仓壁摩擦因数越大,超压因数越大,但贮料和卸料工况下仓壁侧压力均有减小,这表明增大仓壁摩擦因数对筒仓结构受力是有利的。
4 结论
通过对3个不同摩擦因数的模型仓进行贮料及卸料过程的模拟分析,得出以下结论:
(1)筒仓内散体颗粒在静止状态下,在高度方向上仓壁侧压力分布基本与Janssen公式计算值吻合,最大值出现在筒仓底部附近。
(2)卸料过程中,卸料压力峰值需要经过一段时间才会出现,且在增大到峰值的过程中可能会出现在短暂时间内仓壁侧压力减小的情况。侧压力在达到峰值后逐渐减小,且在减小的过程中会出现短暂时间内仓壁侧压力增大的情况。
(3)仓壁摩擦因数对贮料压力和卸料压力峰值的影响程度随着深度的增加而增大。且仓壁摩擦因数越大,其对贮料压力和卸料压力峰值影响越大。
(4)仓壁摩擦因数越大,超压因数越大,贮料压力和卸料压力峰值越小。
[1]俞良群,邢纪波.筒仓装卸料时力场及流场的离散元法模拟 [J].农业工程学报,2000,16(4):15-19.
[2]陈长冰,梁醒培.筒仓卸料过程的离散元模拟分析[J].粮油食品科技, 2008,16(1):11-13.
[3]KOBYLKA R, MOLENDA M.DEM sim ulations of loads on obstruction attached to the wallofa modelgrain silo and offlow disturbance around the obstruction[J].Powder Technology, 2014, 256:210-216.
[4]刘定华,郭明昌,杨建斌.筒仓仓壁动态压力的测试和分析 [J].西安冶金建筑学院学报,1989(1):108-113.
[5]李国柱,刘定华.筒仓动态压力的计算和测试[J].宁波高等专科学校学报,2000(4):1-7.
[6]王军,何迎春,孙红亮.散体物料对筒仓结构动力响应影响的离散元数值模拟[J].河南工业大学学报(自然科学版), 2009,30(2):74-77.
[7]曾长女,于航.基于线性接触模型的小麦三轴试验细观模拟[J].河南工业大学学报(自然科学版),2015, 36(2):66-70.
[8]徐泳,KAFUI K D,THORNTON C.用颗粒离散元法模拟料仓卸料过程[J].农业工程学报,1999,15(3):65-69.
[9]WEINHART T,LUDING S,LABRA C,et al.Influence of coarse-graining parameters on the analysis of DEM simulations of silo flow[J].Powder Technology, 2016,293:138-148.
[10] MOYSEY P A,RAO N V R,BAIRD M H I, et al.Dynamic coefficient of friction and granular drag force in dense particle flows:Experiments and DEM simulations[J].Powder Technology,2013,248:54-67.
[11] LI Y,GUI N, YANG X ,et al.Effect of friction on pebble flow pattern in pebble bed reactor [J]. Annals of Nuclear Energy,2016,94:32-43.
[12] 戚迎花.散储粮储藏容重与若干影响因素的关系试验研究及离散元模拟[D].郑州:河南工业大学,2014.
[13] 陈长冰.筒仓内散体侧压力沿仓壁分布研究[D].合肥:合肥工业大学,2006.
[14] 肖昭然,王军,何迎春.筒仓侧压力的离散元数值模拟[J].河南工业大学学报(自然科学版),2006,27(2):10-12.
[15] HAMMADEHH.Science-flow and pressure during centric and eccentric discharge in cylindrical silos[J].Bulk Solids Handling,2012(4) :44-48.
[16] YANG Y, ROTTER M, OOI J,et al.Flow channelboundaries in silos [J].Chemical Engineering Technology, 2011, 34(8):1295-1302.
[17] VIDAL P, GUAITA M, AYUGA F.Analysis of dynamic discharge pressures in cylindrical slender silos with a flat bottom or with a hopper: comparison with eurocode 1[J].Biosystems Engineering, 2005, 91(3):335-348.
INFLUENCE OF THE WALL FRICTION ON THE LATERAL PRESSURE OF SILO WALL
ZHANG Zhao1,LIU Kejin2, XIAO Zhaoran2, WANG Shihao2
(1.Zhengzhou City Rail Transit Co.,Ltd.,Zhengzhou450002,China;2.College of Civil Engineering and Architecture,Henan University of Technology,Zhengzhou450001,China)
The paper simulated and analyzed the changes of lateral pressure on the wall of silos with different wall friction coefficient under storage and dischage conditions by using discrete element method. Results showed that the peak pressure distrubution on the wall caused by discharge was the control pressure for silo structure design. With the increase of the wall friction coefficient, the overpressure coefficient increased, but the static pressure and the peak discharge pressure on the side wall of silos decreased. The influences of the friction factor on the laterial pressure on the wall were deepened wiht the depth.
silo; discrete element method; friction coefficient;lateral pressure
文献标志码:
1673-2383(2017)05-0088-05
http://kns.cnki.net/kcms/detail/41.1378.N.20171030.0936.032.html
网络出版时间:2017-10-30 9:36:40
2017-06-13
河南工业大学高层次人才基金项目(150597);国家自然科学基金项目(51178165;51708183)
张昭(1979—),男,河南信阳人,博士,高级工程师,研究方向为离散元工程应用。
*通信作者

