电动汽车永磁同步电机滑模低速控制*

郭 栋, 吴 琦, 祁晓野

(1. 辽宁工业大学 电气工程学院,辽宁 锦州 121001;2. 北京航空航天大学 流体传动与控制技术研发中心,北京 100191)

电动汽车永磁同步电机滑模低速控制*

郭 栋1,2, 吴 琦1, 祁晓野2

(1. 辽宁工业大学 电气工程学院,辽宁 锦州 121001;2. 北京航空航天大学 流体传动与控制技术研发中心,北京 100191)

针对采用永磁同步电机id=0矢量控制调速的电动汽车电机驱动控制系统，为了改善其抗负载扰动能力，并且当电动汽车处于低速运行时，能够输出大转矩，将滑模变结构控制中的变指数趋近律进行改进，设计了一种滑模速度控制器。为了减小滑模变结构控制的抖振问题，引入饱和函数来代替符号函数，同时考虑到滑模速度控制器中存在滞后问题，将饱和函数与经过积分环节后得到的信号相乘，在提高了响应速度的同时增强系统的抗扰动能力。经过仿真验证，不同负载工况下，滑模速度控制器具有较强的鲁棒性和抗扰动能力，满足电动汽车低速运行工况下输出大转矩的要求。

滑模变结构控制；永磁同步电机；电动汽车

0 引 言

电机驱动控制系统是电动汽车的心脏，永磁同步电机(Permanent Magnet Synchronous Mortor,PMSM)因其高功率密度、高效率等优势在电动汽车上得到了广泛应用。由于PMSM是一个含有非线性环节以及强耦合的多变量系统，虽然PI控制在一定范围内可以达到控制要求[1-2]，但应用于电动汽车的电机控制时，由于电动汽车低速运行时常常处于如爬坡、频繁地起动停止等复杂运行工况，而PI控制达不到控制性能的要求。为使电动汽车电机驱动系统对负载的抗扰动能力得到改善，并且在低速运行时可以输出大转矩，许多现代控制理论被应用到PMSM调速系统中[3-8], 如模糊控制、神经网络控制和滑模变结构控制等。但是模糊控制的设计尚缺乏系统性，神经网络控制器的理论和学习算法还有待于进一步地完善和提高，而滑模变结构控制对扰动和不确定参数具有较强的鲁棒性，系统的结构根据系统当前状态有目的地实时变化，是一种非常特殊的非线性控制方法，且响应速度快。因此，本文将滑模变结构控制应用于电动汽车的电机驱动控制系统，使其能够满足低速运行时的工况要求和性能指标。

文献[9]针对PMSM，采用了一种改进的指数趋近律，具有抖振小、速度响应快、超调量小等优点,对于PMSM最大转矩电流比(Maximum Torque Per Ampere，MTPA)控制调速系统，文献[10]对滑模变结构控制进行了改进，提高了对参数的自适应能力，增强了对负载抗扰动能力。文献[11]采用了一种指数趋近律，该控制器对转速实现了无超调跟踪，对参数扰动具有较好的鲁棒性。文献[12]采用了一种新型幂次趋近律，并应用于PMSM的矢量控制系统，其控制精度和调速性能良好，可以很好地抑制外部扰动。这些文献中设计的控制器中包含的积分项，虽然可以削弱抖振现象以及消除系统的稳态误差，但并未考虑到引入积分环节后导致的滞后问题。

本文采用饱和函数代替符号函数解决滑模变结构控制中的抖振问题，同时采用饱和函数与经过积分环节运算后得到的信号相乘的方法解决控制器中引入积分环节导致的滞后问题。经过仿真验证，所设计的控制器提高了系统的鲁棒性，具有良好的动态、静态性能。

1 PMSM数学模型

本文研究中对PMSM作如下假设：

(1) 电机的转子磁场以正弦波的方式分布于气隙空间中；

(2) 感应电动势为正弦波；

(3) 磁路为线性，忽略铁心饱和、铁心涡流以及磁滞损耗的影响。

采用id=0矢量控制策略，PMSM在d-q旋转坐标系下的电压方程为[13]

式中:ud、uq——d、q轴电压；

id、iq——d、q轴电流；

Ld、Lq——d、q轴电感；

ψf——永磁体磁链；

Rs——定子相电阻；

ω——转子电角速度。

PMSM的电磁转矩方程为

PMSM的运动方程为

式中:Te——电磁转矩；

TL——负载转矩；

p——PMSM的极对数。

2 速度控制器的设计

2.1状态空间方程的建立

选取PMSM控制系统状态变量为

式中:ω*——给定转速；

ω——实际转速。

结合式(2)～式(4)可得

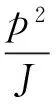
2.2滑模面的选取

为满足使系统无超调达到稳定的要求，选取一阶线性滑模面s=cx1+x2(c>0，为待设计参数)，并对其求导，得

2.3趋近律的选取

趋近律控制方法可以保证趋近运动的动态品质,使控制系统获得良好的控制效果。由于指数趋近律只能在原点附近来回抖振，变速趋近律则会趋近并稳定于原点，而变指数趋近律[10]是将指数趋近律与变速趋近律相结合，吸收二者的优点，其表达式为

式中:q——指数趋近律系数，q>0;

ε|x1|——变速趋近律系数，ε>0。

由式(8)可知，滑模面外的轨迹，是按指数增长的方式向滑模面运动的；当快要到达滑模面时，变速项-ε|x1|sgn(s)起主要作用；当到达滑模面时，因为转速误差和滑模面运动过程的关系，会导致运动幅度逐渐减小，趋近于原点。

2.4稳定性分析

根据Lyapunov理论，滑模变结构控制的存在性和可达性满足如下关系：

式中:V(x)——Lyapunov函数，V(x)=(1/2)s2；

s≠0。

将式(8)代入式(9)，得

无论s取何值，满足存在性和可达性条件，即式(10)始终成立。

2.5控制律的求取

根据选取的趋近律并结合式(7)得控制器输出的表达式为

从而可得q轴电流的给定值为

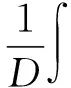
2.6改进的控制律

因为sgn(s)函数是一种不连续型函数，故导致系统出现抖振现象。为了削弱系统的抖振问题，这里引入饱和函数sat(s,δ)代替式(12)中sgn(s)函数，由于sat(s,δ)·s与sgn(s)·s的符号特性相同，故根据式(10)满足稳定性条件。

饱和函数sat(s,δ)的表达式为

其中，δ为较小的正常数，但不宜过小。如果δ取值太小，则会导致抖振问题。

所以，

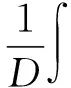
另外，为了解决积分环节引起的滞后问题，本文将控制律作了改进，即

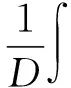
3 仿真结果与分析

图1 系统仿真模型结构框图

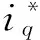
本文研究对象为：价格在5～8万元的电动汽车。通过查找相关方面的资料，选用的PMSM参数如表1所示。

表1 PMSM参数

3.1不同负载起动工况分析

为了验证本文所设计的滑模速度控制器的控制性能，设计了以下三种工况的仿真来验证，即轻载起动、额定负载起动和重载起动。

图2 不同负载起动工况下的速度响应曲线

在t=0 s，转速为3 000 r/min，起动转矩分别为5、24、40 N·m时，各种工况下传统PI控制与滑模变结构控制的速度响应曲线如图2所示。其中，24 N·m是额定转矩；当转矩为40 N·m时，电机转速仅为1 800 r/min，达不到3 000 r/min。

从图2可以得到表2中的数据。经分析知所设计的滑模速度控制器响应速度快，响应曲线很平滑、无超调，因此，采用滑模控制得到的控制效果更佳，并且缩短了响应时间。

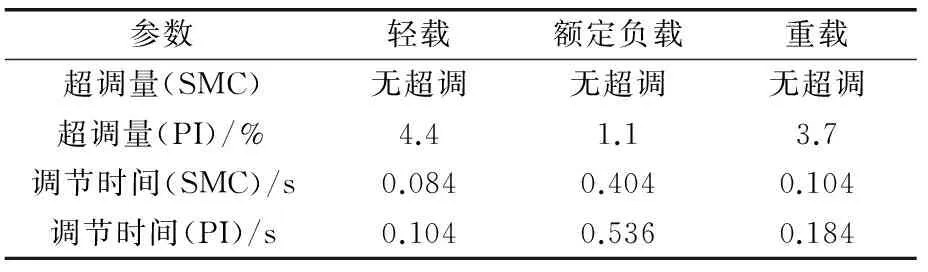
表2 不同工况不同控制策略下性能参数

3.2不同负载干扰工况分析

在额定负载起动的情况下，针对不同的负载干扰情况进行仿真，验证控制器的控制性能。

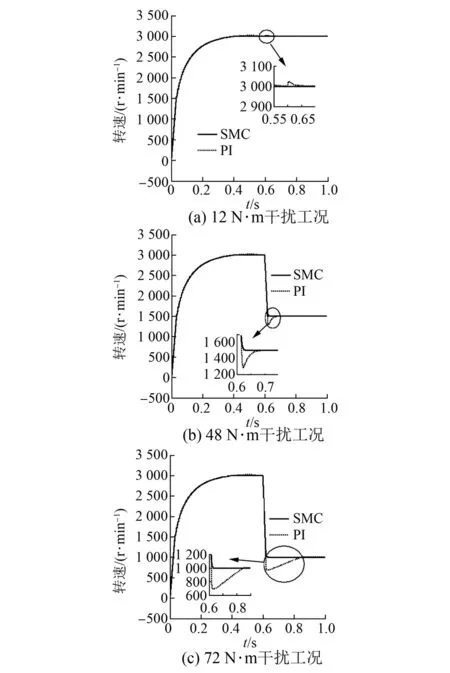
图3 不同干扰工况下的速度响应曲线

在t=0 s、转速为3 000 r/min、起动转矩为24 N·m的起动条件下，当t=0.6 s时，设置以下三组干扰转矩和转速，即：12 N·m和3 000 r/min、48 N·m和1 500 r/min、72 N·m和1 000 r/min。此时，各工况下传统PI控制与滑模变结构控制的速度响应曲线如图3所示。

从图3可以得到表3中的数据，经分析知与PI控制相比，所设计的滑模速度控制器对负载干扰有更好的抑制能力，提高了系统的鲁棒性。

表3 突加干扰不同控制策略下性能参数

3.3改进的控制律的有效性分析

在t=0 s、转速为3 000 r/min、起动转矩为5 N·m时，控制律表达式(15)中积分环节后的信号与饱和函数是否相乘的速度响应曲线，如图4所示。

图4 改进的控制律速度响应曲线

由图4可知，当滑模控制中参数都设定为c=100、ε=10、q=50时，将饱和函数与经过积分环节得到的信号相乘，采用这种方法设计的速度控制器控制性能更好、响应速度快、稳定性好；而没有与饱和函数相乘的方法，响应有一定的超调，约为4.4%。但将参数由c=100改为c=80时，控制器的调节时间较慢。因此，将饱和函数与经过积分环节得到的信号相乘的控制方法可以很好地解决积分环节引起的滞后问题。

4 结 语

本文将改进的变指数趋近律的滑模变结构控制策略应用于电动汽车PMSM的id=0矢量控制调速系统，设计了PMSM的滑模速度控制器。在控制方法中，采用饱和函数代替符号函数，减弱了滑模变结构控制的抖振现象；并且将饱和函数与经过积分环节得到的信号相乘，在一定程度上，解决了积分环节引起的滞后问题。仿真结果表明，本文所设计的PMSM滑模速度控制器改善了电机驱动控制系统的抗负载扰动能力，提高了系统的鲁棒性，满足了电动汽车低速运行时输出大转矩的工况要求，同时说明了本文所提出的控制策略具有可行性和优越性。

[1] 孙强,程明,周鹗,等.新型双凸极永磁同步电机调速系统的变参数PI控制[J].中国电机工程学报,2003,23(6): 117-123.

[2] LAI C K, SHYU K K. A novel motor drive design for incremental motion system via sliding-mode control method[J]. IEEE Trans on Industrial Electronics, 2005,52(2): 499-507.

[3] BOSSANYI E A. GH bladed theory manual[R]. UK-Bristal: Grand Hassan and Partner Limited,2009: 13-36.

[4] MOHAMED A R I. Adaptive self-tuning speed control for permanent-magnet synchronous motor drive with dead time[J].IEEE Transactions on Energy Conversion,2006,21(4): 855-862.

[5] SHEN Y X, WU D H, JI Z C. Model reference fuzzy adaptive control of permanent magnet synchronous motor[C]∥ Proceeding of the Chinese Control Conference, 2006: 1522-1527.

[6] EL-SOUSY F F M. High-performance neural-network model-following speed controller for vector-controlled PMSM drive system[C]∥ IEEE International Conference on Industrial Technology, ICIT’ 04, 2004: 418-424.

[7] 李晨丹,黄文新.基于遗传算法的永磁同步电动机矢量控制系统的优化设计[J].微电机,2012,45(5): 73-76.

[8] 龚贤武,徐淑芬,张丽君,等.永磁同步电机模糊自适应补偿速度控制系统[J].计算机仿真,2014,31(1): 356-360.

[9] 胡耀华,刘闯,宁银行.永磁同步电机改进型指数趋近率滑模控制[J].微电机,2012,45(8): 54-57.

[10] 金宁治,王旭东,李文娟.电动汽车PMSM MPTA控制系统滑模速度控制[J].电机与控制学报,2011,15(8): 52-58.

[11] 张宏达,贾贵玺,郭锦波,等.永磁同步电机的趋近律滑模控制[J].重庆理工大学学报(自然科学),2015,29(3): 89-94.

[12] 刘庆华,吕永健,阳杰.电动汽车PMSM滑模变结构控制[J].计算机仿真,2015,32(12): 129-132.

[13] 张晓光,赵克,孙力,等.永磁同步电机滑模变结构调速系统动态品质控制[J].中国电机工程学报,2011,31(15): 47-52.

SlidingModeLowSpeedControlofPMSMforElectricVehicle*

GUODong1,2,WUQi1,QIXiaoye2

(1. School of Electrical Engineering, Liaoning University of Technology, Jinzhou 121001, China;2. R&D Centre of Fluid Power Transmission & Control Technology, Beihang University, Beijing 100191, China)

Aiming at the motor drive control system of electric vehicle for using permanent magnet synchronous motor with vector control, in order to improve its capability of resisting load disturbance, and when the electric vehicle was running at low speed, it could output large torque. A sliding mode speed controller was designed to improve the exponential reaching law of sliding mode variable structure control. In order to reduce chattering of the sliding mode variable structure control, the saturation function was introduced instead of the sign function. At the same time, considering the hysteresis in sliding mode speed controller, the saturation function and the integral signal are multiplied, so that the response speed could be improved and the disturbance rejection capability could be enhanced. Simulation results showed that when the load was changed, the sliding mode speed controller had strong stability, which could made the electric vehicle output large torque at low speed.

slidingmodevariablestructurecontrol;permanentmagnetsynchronousmotor(PMSM);electricvehicle

国家自然基金项目(51275021);辽宁省自然科学基金指导计划项目(201602370);辽宁省教育厅科学研究一般项目(L2015229)

郭 栋(1976—)，男，副教授，研究方向为电机驱动与控制、液压伺服控制、嵌入式系统设计。

吴 琦(1990—)，男，硕士研究生，研究方向为现代电力电子应用技术。

祁晓野(1961—)，男，副教授，研究方向为液压伺服控制、电机驱动与控制。

TM 301.2

A

1673-6540(2017)10- 0119- 05

2016 -12 -20