推本溯源 就式论式
——浙江省高考数列压轴题的解题突破
● (温州市第二十一中学,浙江 温州 325000)
2017-07-03
许光军(1968-),男,浙江温州人,中学高级教师.研究方向数学教育.
推本溯源就式论式
——浙江省高考数列压轴题的解题突破
●许光军
(温州市第二十一中学,浙江 温州 325000)
浙江省数学高考连续3年都以数列不等式的综合题作为压轴.文章剖析2017年浙江省数学高考的压轴题,推本溯源,归纳出数列不等式的解题突破——就“式”论“式”,并用“就式论式”的思路突破浙江省近几年的数列不等式压轴题,为新一轮的高三数学复习备考,提供一个启迪思维、探究解法的视角.
数列压轴题;就式论式;转化变形
数列不等式综合题是以数列知识为背景,以数列的通项、递推公式、前n项和为载体,考查数列的构造、求和、等价转化以及不等式的证明.由于题目条件结构简明,知识交汇丰富,思维跨度较大,能力辐射面广,思想方法渗透自然,具有较好的选拔功能,常常作为高考卷或模拟卷中的压轴题出现.
解答数列不等式综合题,对学生的数学思维能力和常用的数学思想方法应用要求较高,相应的题目难度也比较大.特别是近几年的浙江省数学高考压轴题,题目简明单一,条件变形灵活,学生在解答时,不知从何入手.对于大多数学生来说,更多的是用不完全归纳法做一点浅层次地解答,甚至直接放弃,非常可惜.笔者剖析浙江省近几年的数列不等式的压轴题,试图以题目结论为目标,就“式”论“式”,对题目条件进行有针对性地转化、变形,推本溯源,寻找这类数列不等式压轴题的解题突破.
1 2017年浙江省高考压轴题的“就式论式”
例1已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(其中x∈N*),证明:当n∈N*时,
1) 0 (2017年浙江省数学高考理科试题第22题) 要证0 1.1 第1)小题的分析 要证明0 xn-xn+1=ln(1+xn+1). 方法1分类讨论 若xn+1=0,则xn=xn+1=0,与x1=1矛盾; 若xn+1<0,则xn-xn+1=ln(1+xn+1)<0,即xn+1>xn,从而xn+1>xn>…>x1=1,矛盾; 若xn+1>0,则xn-xn+1=ln(1+xn+1)>0,即xn+1 方法2直接应用不等式 可得xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1, 从而 因为x1=1,所以 又xn+1>0且xn-xn+1=ln(1+xn+1)>0,故0 1.2 第2)小题的分析 xn=xn+1+ln(1+xn+1)≥ 1.3 第3)小题的分析 xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1, 从而 因为x1=1,所以 即 从而 于是 故 下面以浙江省高考最近两年的数列不等式压轴题为例,进一步说明“就式论式”的解题突破. (2015年浙江省数学高考理科试题第22题) 累加可得 因此 这是本题的难点所在,也是解答本题的关键.对比例1的解题过程,例2的变形更加灵活. 1)证明:|an|≥2n-1(|a1|-2); (2016年浙江省数学高考理科试题第22题) 从而 于是 即 |an|≥2n-1(|a1|-2). 于是 即 |an|≤2. 评注累加是解决本题的关键.与例2相比,例3的条件变形没有那么多样,而是把条件的等价变形式向两个方向累加,这是凸显学生解题能力的亮点.两个小题,一正一反两个方向,方法富有哲理,给人以茅塞顿开的启迪. 回看2008年浙江省数学高考压轴题,如果用“就式论式”的视角来看,解题的突破口也非常自然可以找到. 1)an 2)Sn>n-2; 3)Tn<3. (2008年浙江省数学高考理科试题第22题) 2)要证Sn>n-2,将其变形为Sn-n>-2,即证 (a1-1)+(a2-1)+…+(an-1)>-2. (a1-1)+ (a2-1)+…+(an-1)= 由第1)小题可知an<1,从而 于是Sn>n-2. 即 从而 找到解题的突破,于是 就式论式,向目标靠近,寻求解题突破的本源. 由4年浙江省数学高考压轴题分析可知:在数列不等式的求解中,数列求和、不等式的放缩等技巧仅仅是求解过程的某个环节.高考中的数列压轴题,更加注重能力立意,全方位地考查数学思维能力,面对这类试题,重复的题海训练往往感到乏力.在解题教学中,指导学生立足题目的结论,探究题目条件等价变形的方向,就式论式,推本溯源,才是一种有效的选择. 从整个数学问题的求解来看,解题的本质,就是从题目的条件到题目结论建立起逻辑联系,平时在教学中常提的一些数学思想方法,都是达成这种联系的必要工具,学生的数学思维和数学能力,具体体现在建立这种联系的过程中.从这一点上来看,“就式论式”不仅仅是数列不等式的解题突破,也可以为新一轮高三数学复习备考中“如何启迪思维,怎样提升数学素养,探求解题本源”提供一个新的视角. [1] 蔡小雄.更高更妙的高中数学思想与方法[M].杭州:浙江大学出版社,2012. [2] 卢明.稳中求变 体现创新——2015年浙江数学高考理科数列试题评析[J].中学教研(数学),2015(8):23-27. [3] 许光军.如何从n=k到n=k+1[J].高中数学教与学,2008(10):3-5. O122 A 1003-6407(2017)10-41-04

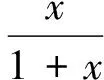
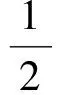
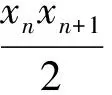
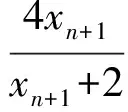

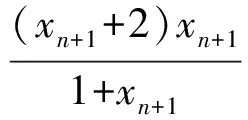

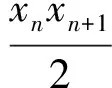

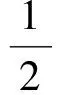
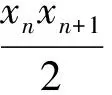
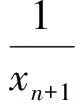
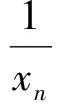
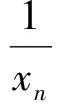
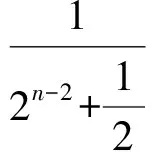
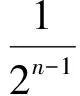
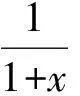
2 “就式论式”突破2015年和2016年的高考压轴题

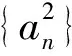
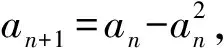
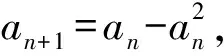
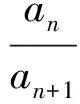
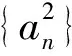


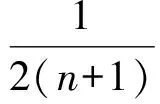

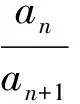

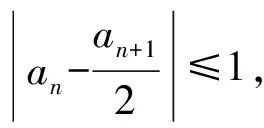
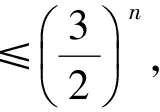

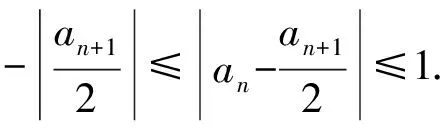
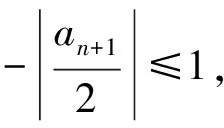



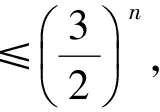


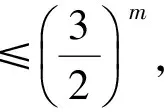



3 2008年高考压轴题的再“论式”