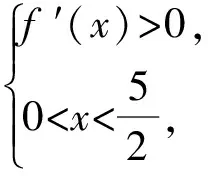对2017年全国卷Ⅰ理科第16题的寻源探变

● (虞阳中学,福建 福清 350307)

2017-07-28

教育部福建师范大学基础教育研究中心2017年开放课题(KC-2017053)

汤小梅(1971-)，女，福建福清人，中学高级教师.研究方向数学教育.

对2017年全国卷Ⅰ理科第16题的寻源探变

●汤小梅
(虞阳中学,福建 福清 350307)

高中数学应用一题多解与一题多变的方法，让学生将所学知识进行灵活运用，并开拓思路，从而做到融会贯通．这就需要我们面对数学试题，学会多角度欣赏与思考，从中发现试题的解决规律，并能寻“根”探“源”与同“源”探“变”，进而掌握一类题的应对策略．

一题多解;寻根探源;同源变式

1 试题展现

例1如图1，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边△ABC的中心为O．D,E,F为⊙O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得点D,E,F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为______．

(2017年全国数学高考卷Ⅰ理科试题第16题)

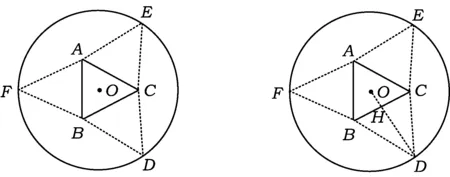
图1 图2

点评这道高考题文字表述流畅、图像优美，令人赏心悦目．借用平面图形的翻折为背景，考查利用导数解决三棱锥体积的最大值问题，意在考查学生的空间想象能力、转化和化归能力、实际应用能力以及运算求解能力．在近5年的新课标试卷中，利用导数解决最优化问题是首次考查，此类考题规避了特殊技巧，凸现了数学本质，能有效地考查学生的创新意识，培养学生的应用意识．

2 解法探究

从而三棱锥的高为

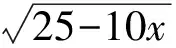
于是

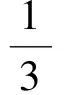
f′(x)=20x3-10x4.

f(x)max=f(2)=16，

于是

解法2联结OD,交BC于点H(如图2),设AB=2x，则

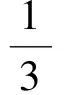
从而三棱锥的高为

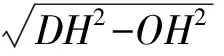
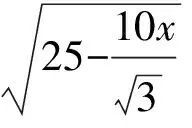
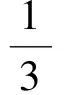
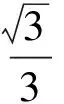
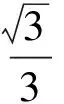
点评在上述的两种解法中，解法1是常规解法，为大多数学生所选．通过观察已知图形特征，设弦心距为x，快速找到三棱锥的体积是关于x的函数，借用“导数”的工具性，通过求导，判断函数的单调性，求出三棱锥体积的最大值．注意隐蔽条件“自变量在实际意义中的取值范围”在解题中的应用．解法2设正三角形的边长为2x，求出三棱锥的体积关于x的函数，借用“5个正数的算术—几何平均不等式”(也称基本不等式的推论)，展现了基本不等式的推论在求最值中的威力和魅力，充分显示了解法的灵活性，实属巧思妙解，干净利落，意犹未尽．

3 寻根探源

图3 图4

例2[1]一块边长为10 cm的正方形铁片按如图3所示的阴影部分裁下，然后用余下的4个全等的等腰三角形加工成一个正四棱锥(底面是正方形，从顶点向底面作垂线，垂足是底面四棱锥的中心)形容器(如图4)，试把容器的容积V表示为x的函数．

(人教A版《数学(必修2)》第37页复习参考题B组第4题)

例3[2]用半径为R的圆形铁片剪出一个圆心角为α的扇形，制成一个圆锥形的容器，问：扇形的圆心角α多大时，容器的容积最大？

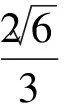
(人教A版《数学(选修2-2)》第67页复习参考题B组第3题)

例1是例2和例3的整合：只需把“圆形铁皮或正方形铁片”变为“圆形纸片”，把“围成圆锥或四棱锥”变为“三棱锥”，并把结论“容器的容积最大时的自变量的值或容积V表示为x的函数”变为“求三棱锥体积的最大值”，即得例1．在强调命题改革的今天，通过改编、创新等手段来赋予课本例题、习题新的生命，这已成为高考命题的一种新走向．近几年高考试题的命制越来越新颖多变，尤其是对不等式的考查，形式多样，但万变不离其宗，大多数高考题都能在课本中找到其原型.因此，我们在高三复习备考的过程中要注意对课本例题、练习题的训练，把握其实质，掌握其规律，规范其步骤，做到“胸中有本”.

4 同源变式

俗话说：“铁打的营盘，流水的兵．”高考中不变的是知识，变化的是情景的呈现形式、问题的结构方式．这就要求我们面对数学题能突破常规，陈题巧改编，旧瓶装新酒．

思考1把例1的背景精雕细琢，变为实际生活中的应用问题，并把“圆形纸片的半径为5 cm”变为“圆形包装纸的半径为10 cm”，便可得到如下立意新颖、构思独特的好题[3]：

图5

变式1某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10 cm的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点(如图5)．设正三棱锥的底面边长为xcm，体积为Vcm3，在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是______，此时x的值为______．

思考2去掉高考题中的图形的翻折背景，并把条件中的“正三棱锥”变为直接呈现“正四棱锥”，并添加条件“侧棱长为1”，结论还是“求体积的最大值”，即可得到如下题意简洁、清晰的好题：

变式2设正四棱锥的侧棱长为1，则其体积的最大值为______．

分析设正四棱锥的底面边长为x，则体积为

设x2=t(其中0

y=t2(2-t)=2t2-t3，

从而

y′=4t-3t2=-t(3t-4)，

思考3仍用例1的背景，只是把条件与结论中的“三棱锥”变为“四棱锥”，即可得如下“新口味”的好题：

变式3如图6，圆形纸片的圆心为O，半径为5 cm，该纸片上的正方形ABCD的中心为O．E,F,G,H为⊙O上的点，△EAB,△FBC,△GCD,△HDA分别是以AB,BC,CD,DA为底边的等腰三角形．沿虚线剪开后，分别以AB,BC,CD,DA为折痕折起△EAB,△FBC,△GCD,△HDA，使得点E,F,G,H重合，得到四棱锥．当正方形ABCD的边长变化时，所得四棱锥体积(单位：cm3)的最大值为______．

图6 图7

分析联结OE，交AB于点M(如图7)，则OE⊥AB.设OM=x，则BC=2x，EM=5-x,从而四棱锥的高为

且

S正方形ABCD=4x2,

f′(x)=20x3-10x4.

f(x)max=f(2)=16，

于是

由上可知:课本素材是高考考题编拟的蓝本，对高考典型试题进行多角度思考，实际上是对高考试题的“二次开发”，即通过一道题，明晰一类题．对典型试题，尤其是涉及核心知识内容的典型试题的剖析和思考更是必不可少，通过对典型试题的灵活变换和多角度思考，展开问题的来龙去脉和知识间的纵横联系，让学生站在一定的高度去思考问题，突出数学的本质，使学生的思维得到提升，使知识达到融会贯通.如此，不论高考题的构思多么新颖，学生也能做到以不变应万变．

[1] 课程教材研究所.普通高中课程标准实验教科书·数学(必修2)[M].北京：人民教育出版社，2016：37.

[2] 课程教材研究所.普通高中课程标准实验教科书·数学(选修2-2)[M].北京：人民教育出版社，2014：67-67.

[3] 编写组.2017高考数学经典题型与变式[M].北京：西藏人民出版社，2016.

O123

A

1003-6407(2017)10-38-03