对一道向量最值高考试题的三重研究
● (阳新县高级中学,湖北 阳新 435200)
2017-08-01
邹生书(1962-),男,湖北阳新人,中学高级教师.研究方向数学教育.
对一道向量最值高考试题的三重研究
●邹生书
(阳新县高级中学,湖北 阳新 435200)
2017年全国数学高考新课标卷Ⅲ理科第12题,是一道以平面几何图形为背景、以向量线性表示的等式为呈现方式,求线性系数和最大值的试题.试题在能力立意方面是一道值得深入研究的佳题,文章从一题多解、结论拓展和多题一法这3个方面对这道试题进行了三重研究.
向量;线性表示;最值;高考题;研究
2017年高考已尘埃落定,“研究高考试题,探寻高考新动向,指导高中教学和复习备考”是一线教师面临的重大课题.全国数学高考新课标卷Ⅲ理科第12题是一道以平面向量为载体求最大值的试题,题目能力立意平中见奇,思路入口宽,解法灵活多样,既能很好考查考生对基础知识、基本技能、通性通法的掌握情况,同时考查综合运用多种数学思想如化归转化思想、数形结合思想和函数方程思想分析问题和解决问题的能力,又能有效考查考生运算求解、推理论证和灵活选择解题策略的能力.下面笔者谈谈对这道试题从解法到问题推广,再到这类问题的求解通法的三重研究,希望对读者有所帮助.

( )
1 解法研究,探求一题多解
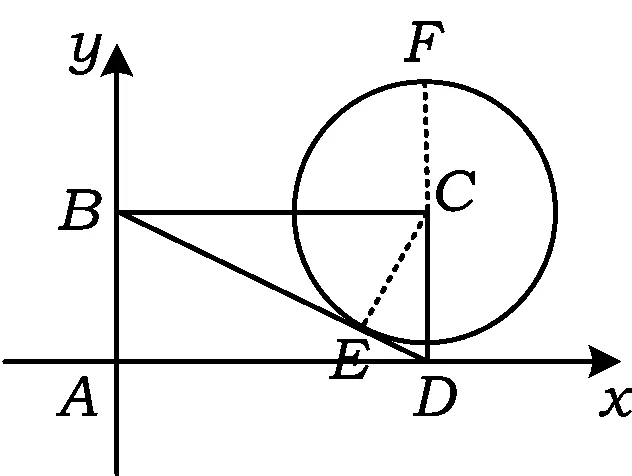
图1
建立如图1所示的直角坐标系,设⊙C与BD相切于点E,联结CE,则CE⊥BD.由面积法得圆的半径为
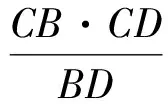
解法1(特殊点法)延长DC交⊙C于点F,则
由题意,得
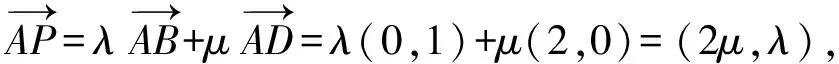
当动点P为点F时,
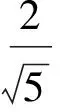
于是
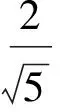
此不等式可用分析法证明.选项B,C,D均不正确,故选A.
解法2(用三角函数求最值)设P(x,y),则
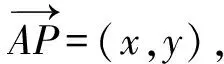
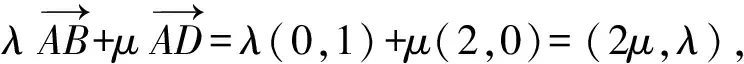
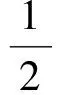
于是
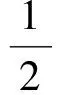
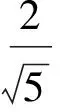
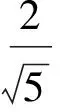
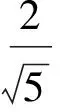

故选A.
解法3(利用直线与圆的位置关系)由解法2得
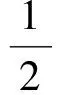
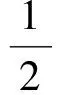
x+2y-2z=0,
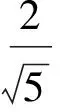
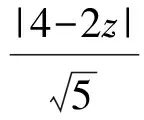
亦即
|z-2|≤1,
解得1≤z≤3.故选A.
解法4(利用线性规划的思想方法)由解法2得
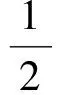
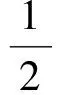
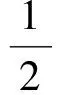
此方程表示经过点P的动直线,其中z就是直线在y轴上的截距.由图1知:当直线与⊙C相切时,z分别取到最大值和最小值,此时圆心到直线的距离等于半径,即
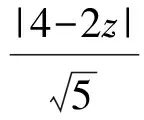
亦即
|z-2|=1,
解得z=1或z=3.其中z=3为最大值.故选A.
点评上述4种解法的共同特点是坐标法,即通过建立直角坐标系将向量问题通过坐标运算转化为代数问题来处理,即用向量的代数特征求解.下面用向量的几何特征再给出一种向量解法.

图2
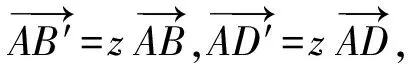
又点P,D′,B′共线,从而
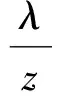
则
z=λ+μ.

2 纵向研究,探索本质属性
试题中的矩形较为特殊,λ+μ的最大值和最小值是否与矩形的形状或大小有关?通过纵向研究发现:λ+μ的最大值和最小值均为定值,与矩形的形状和大小无关,性质与证明如下:

解法1(从圆的参数方程切入,用三角函数求最值)建立如图1所示的直角坐标系,设⊙C与BD相切于点E,联结CE,则CE⊥BD.由面积法得圆的半径为
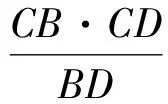
设点P(x,y),则

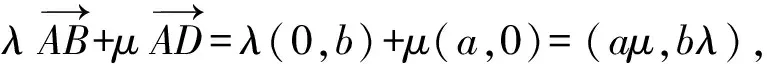

则

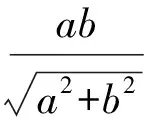
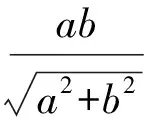
所以

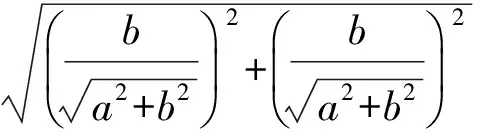
故λ+μ的取值范围是[1,3].
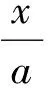
bx+ay-abz=0,
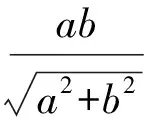
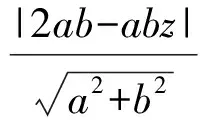
亦即
|z-2|≤1,
解得
1≤z≤3,
故λ+μ的取值范围是[1,3].
解法3(利用线性规划的思想方法)由例1的解法2可得



此方程表示经过点P的动直线,其中bz就是直线在y轴上的截距.由图1知:当直线与圆相切时,bz分别取到最大值和最小值,从而z分别取到最大值和最小值.此时圆心到直线的距离等于半径,即
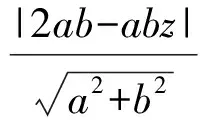
化简得
|z-2|=1,
解得z=1或z=3.故λ+μ的取值范围是[1,3].
解法4(向量方法)与例1的解法5类似,这里从略.
3 横向研究,探寻通性通法
将这道高考题的几何背景一般化,可得如下一般性问题:
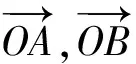
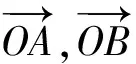
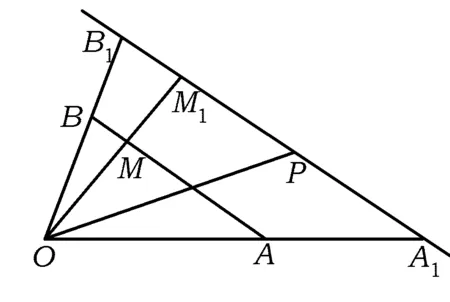
图3
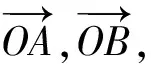
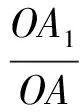
当直线l与AB在点O的两侧时,
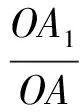
证明因为AB∥A1B1,所以
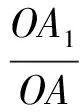
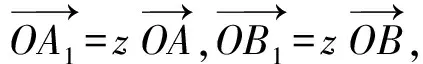
又因为点P,A1,B1共线,所以
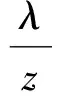
则
λ+μ=z.
当直线l与AB在点O的同侧时,z>0,则
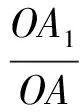
当直线l与AB在点O的两侧时,z<0,则
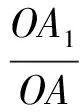
下面举例说明直接运用等高线定理可简单快捷地解答这类问题.
例3在ABCD中,E,F分别为CD,BC的中点,若其中λ,μ∈R,则λ+μ=______.
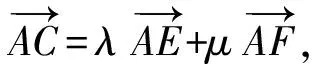
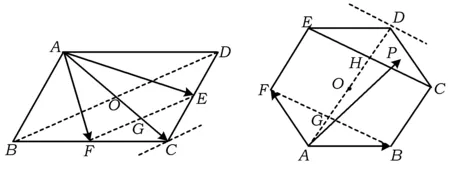
图4 图5
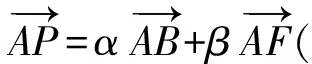
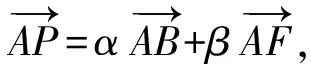

(2011年江西省南昌市数学联考试题)
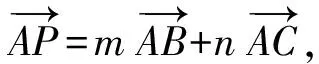

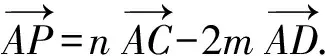
过点P作CD的平行线l,由定理1知:当点P与点C重合时,
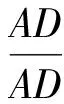
当点P与点B重合时,

又因为P是△ABC内任一点,所以n-2m的取值范围是(-2,1).
点评本解法需要根据所求最值式n-2m构造新基底,灵活运用定理1,从而使问题获解.
图6 图7

(2012年全国高中数学竞赛湖北省预赛高一试题第7题)
解如图7,联结OA,OB,因为O是△ABC的内心,所以OA,OB分别平分∠BAD和∠ABC.延长BO交AC于点D,因为AB=BC=2,所以点D是线段AC的中点.作OE∥BC交AC于点E,因为AO是△ABD的内角平分线,由三角形内角平分线性质定理得
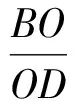
由OE∥BC,得
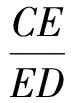
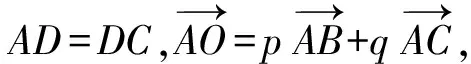
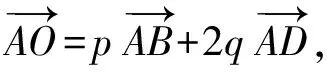
又点B,O,D共线,所以
由式(1)和式(2),得

故
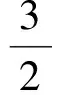

( )
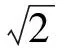
(2013年安徽省数学高考理科试题第9题)

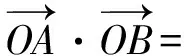
从而

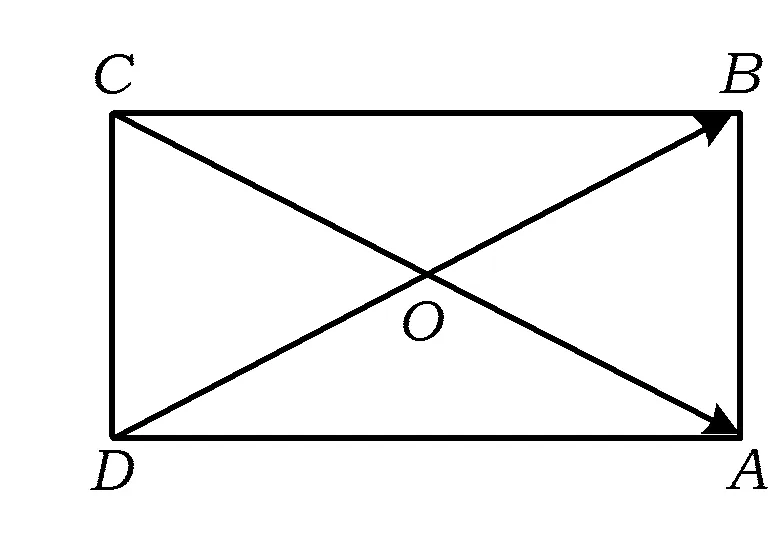
图8

S= 4S△OAB=


故选D.
评注上述向量解法本质上与二元线性规划问题中求线性目标函数的最值或取值范围的图解法完全类似,用的都是平行线法,如果最值存在,其值都在可行域的边界上取得.用平行等高线法求这类问题的值域,对学生来说确实理论要求较高,但起点高落点低,解法形象直观,一旦掌握则答案唾手可得.
笔者对例1进行了3个维度的研究:1)试题解法研究,即一题多解,多角度、多方位用多种数学知识和思想方法解决试题,在高三复习备考时可达到以点带面、做一题复习一大片的效果;2)对试题纵向研究,即将题目的部分条件一般化研究一般性问题的一般性结论,有利于看清问题的本质属性,对问题有比较深刻的理解;3)横向研究,即将问题放到一个更加普遍的一类问题上进行研究,主要研究这类问题的通性通法,达到多题一法、一法解一类题之目的.
[1] 邹生书.构建仿射坐标系解题[J].河北理科教学研究,2012(2):36-39.
[2] 康井荣,苏良国.向量等式转化的几种策略[J].中学数学杂志,2017(5):44-46.
[3] 邹生书.2013年高考平面向量精彩试题赏析[J].数理化学习,2013(10):2-3.
O123.1
A
1003-6407(2017)10-33-05

